Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕОРИЯ ПРИНЯТИЯ РЕШЕНИЙ или ИГРЫ С ПРИРОДОЙ
Содержание
- 1. ТЕОРИЯ ПРИНЯТИЯ РЕШЕНИЙ или ИГРЫ С ПРИРОДОЙ
- 2. В одном небольшом российском городе решили отпраздновать
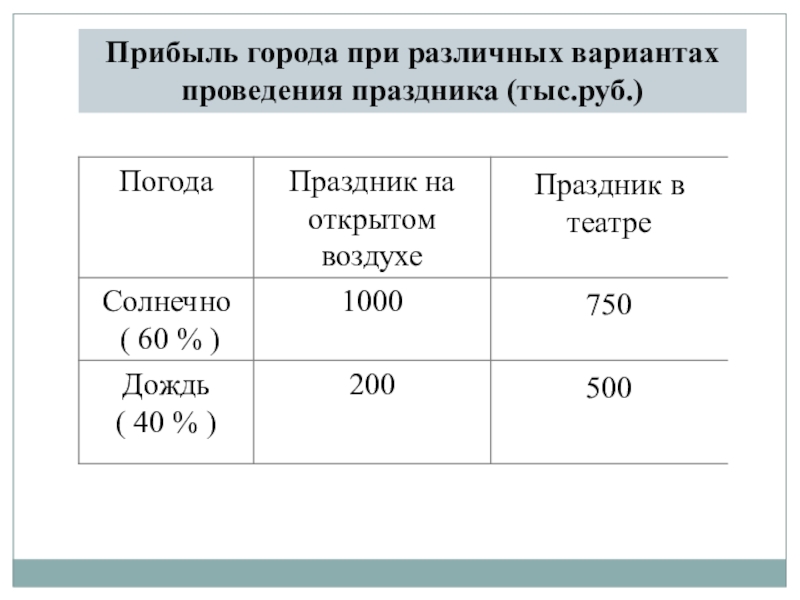
- 3. Прибыль города при различных вариантах проведения праздника (тыс.руб.)
- 4. ВАРИАНТС УЧЕТОМ ВЕРОЯТНОСТИПРАЗДНИК НА УЛИЦЕ: Мы получим:
- 5. ВАРИАНТ «УПУЩЕННАЯ ВЫГОДА»ПРАЗДНИК НА УЛИЦЕ: если пойдет
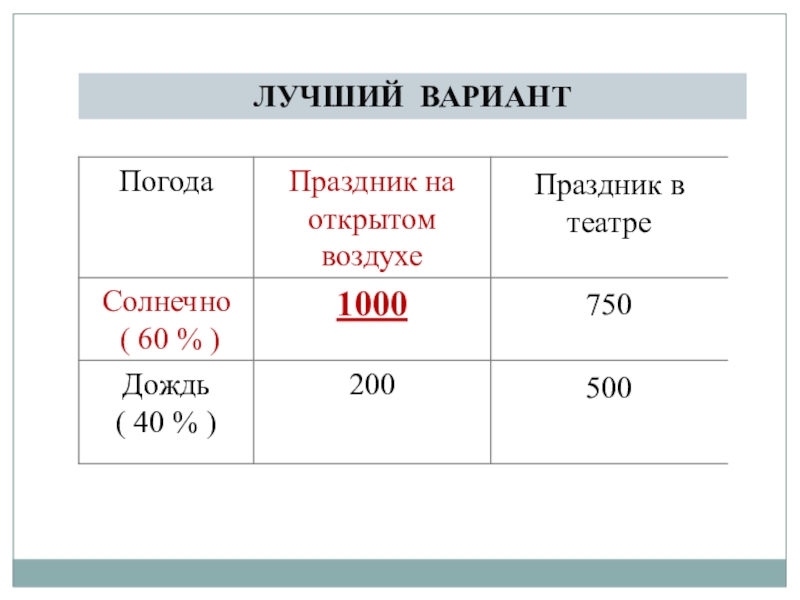
- 6. ЛУЧШИЙ ВАРИАНТ
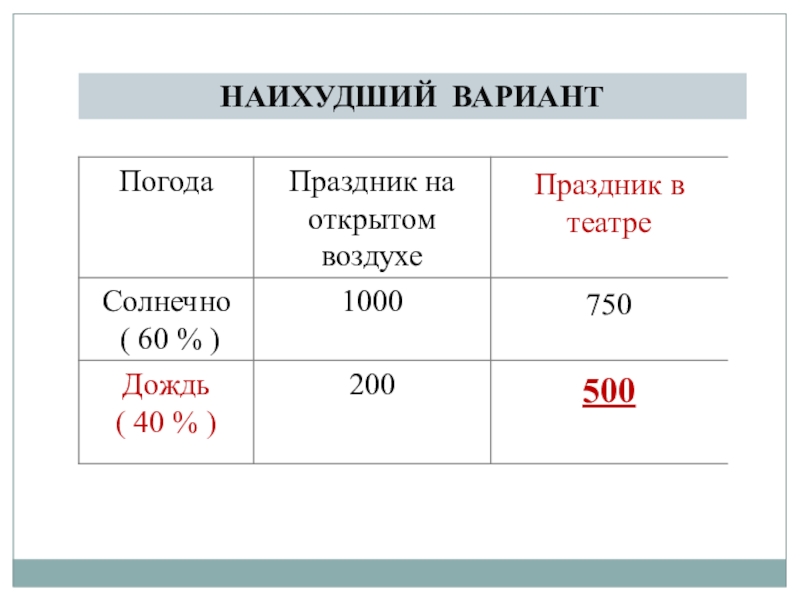
- 7. НАИХУДШИЙ ВАРИАНТ
- 8. Факторы, влияющие на выбор критериев эффективности систем
- 9. Наиболее часто в неопределенной ситуации используются критерии:Среднего
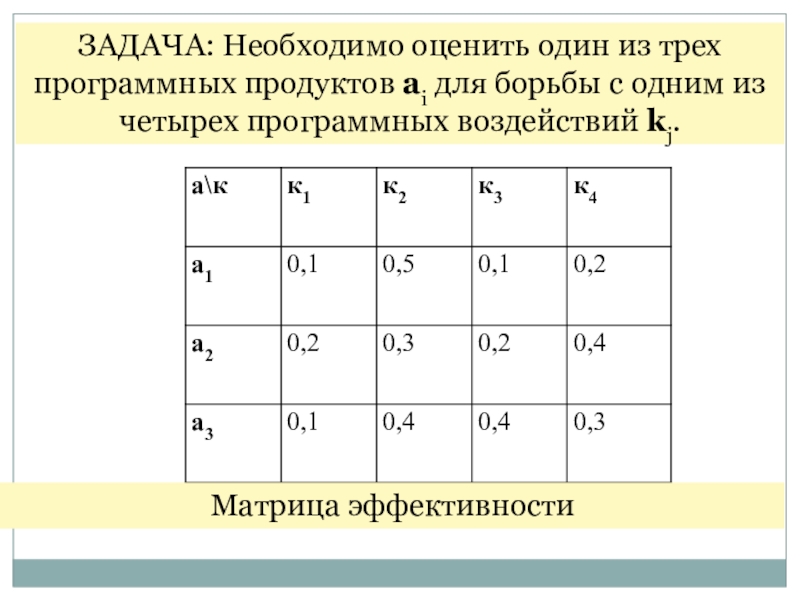
- 10. ЗАДАЧА: Необходимо оценить один из трех программных
- 11. Критерий Байеса(критерий среднего выигрыша)Предположим, что вероятность применения
- 12. Критерий Лапласа (достаточного основания)Предполагается, что состояние обстановки
- 13. Критерий Вальда(критерий осторожного наблюдателя )Это критерий максимального
- 14. Критерий Гурвица(критерий пессимизма-оптимизма )Оценивается самое высокое и
- 15. Критерий Севиджа(критерий минимального риска ) Минимизирует потери
- 16. Критерий Севиджа(критерий минимального риска )МАТРИЦА ПОТЕРЬ Оптимальное значение = минимальное значение К
- 17. Форма записи результатовВывод: выбираем а2 или а3В
- 18. РЕШИТЕ ЗАДАЧУРешено организовать тренажерный зал. По
- 19. Скачать презентанцию
В одном небольшом российском городе решили отпраздновать тысячелетие со дня основания города. Встал вопрос:ГДЕ ПРОВОДИТЬ ПРАЗДНИК ГОРОДА?
Слайды и текст этой презентации
Слайд 2
В одном небольшом российском городе решили отпраздновать тысячелетие со дня
основания города. Встал вопрос:
Слайд 4ВАРИАНТ
С УЧЕТОМ ВЕРОЯТНОСТИ
ПРАЗДНИК НА УЛИЦЕ:
Мы получим:
1000 тыс. в
60% случаев и 200 тыс. в 40% случаев,
значит,
в
среднем 1000 х 0,6 + 200 х 0,4 = 600 + 80 = 680 тыс. 2. ПРАЗДНИК В ТЕАТРЕ:
750 х 0,6 + 500 х 0,4 = 450 + 200 = 650 тыс.
Слайд 5ВАРИАНТ
«УПУЩЕННАЯ ВЫГОДА»
ПРАЗДНИК НА УЛИЦЕ:
если пойдет дождь - упущенная
выгода составит:
500 – 200 = 300 тыс.
2. ПРАЗДНИК В ТЕАТРЕ:
1000–
750 = 250 тыс. 
Слайд 8Факторы, влияющие на выбор критериев эффективности систем в неопределенных ситуациях
а) природа конкретных операций и ее цель
- в одном
случае допустим рискв другом - гарантированный результат
б) причина неопределенности
- закон природы
разумные действия противника
в) характер лица, принимающего решение:
- склонность добиться большего, идя на риск
- всегда осторожные действия
Слайд 9Наиболее часто в неопределенной ситуации используются критерии:
Среднего выигрыша (критерий Байеса)
Достаточного
основания (критерий Лапласа)
Осторожного наблюдателя (критерий Вальда)
Пессимизма-оптимизма (критерий Гурвица)
Минимального риска (критерий
Севиджа)
Слайд 10ЗАДАЧА: Необходимо оценить один из трех программных продуктов аi для
борьбы с одним из четырех программных воздействий kj.
Матрица эффективности
Слайд 11Критерий Байеса
(критерий среднего выигрыша)
Предположим, что вероятность применения противником программных воздействий
Р1 = 0,4; Р2=0,1; Р3=0,1; Р4=0,3
К(а1)=0,4*0,1+0,5*0,2+0,1*0,1+0,3*0,2=0,21
К(а2)=0,4*0,2+0,2*0,3+0,1*0,2+0,3*0,4=0,28
К(а3)=0,4*0,1+0,2*0,4+0,1*0,4+0,3*0,3=0,25
Оптимальное значение = максимальная
сумма ККритерий максимума среднего выигрыша
или минимизации среднего риска.
Слайд 12Критерий Лапласа
(достаточного основания)
Предполагается, что состояние обстановки равновероятно
Р1 =
0,25; Р2=0,25; Р3=0,25; Р4=0,25
К(а1)=0,25*(0,1+0,5+0,1+0,2)=0,225
К(а2)=0,25*(0,2+0,3+0,2+0,4)=0,275
К(а3)=0,25*(0,1+0,4+0,4+0,3)=0,3
Оптимальное значение = максимальная сумма К
NB:
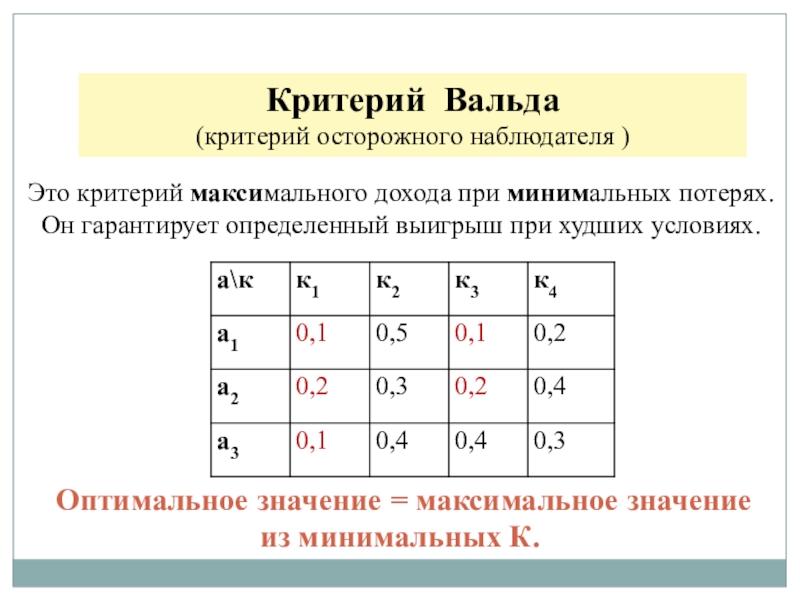
Критерий Лапласа – это частный случай критерия среднего выигрыша
Слайд 13Критерий Вальда
(критерий осторожного наблюдателя )
Это критерий максимального дохода при минимальных
потерях. Он гарантирует определенный выигрыш при худших условиях.
Оптимальное значение
= максимальное значение из минимальных К.
Слайд 14Критерий Гурвица
(критерий пессимизма-оптимизма )
Оценивается самое высокое и самое низкое значение
эффективности и занимается промежуточная позиция.
Оптимальное значение = максимальное
значение взвешенного показателя с помощью коэффициента α сумм максимальных и минимальных оценокК(ai) = α max Kij+(1- α)*min Kij
j j
0≤ α ≤1
К(а1)=0,6*0,5+(1-0,6)*0,1=0,34
К(а2)=0,6*0,4+(1-0,6)*0,2=0,32
К(а3)=0,6*0,4+(1-0,6)*0,1=0,28
На практике используются значения α из интервала (0,3÷0,7)
Слайд 15Критерий Севиджа
(критерий минимального риска )
Минимизирует потери эффективности при наихудших
условиях.
Матрица эффективности преобразуется в матрицу потерь
∆ Кij = maxKij
- Kijразность между максимальным и текущим значениями оценок эффективности в столбце
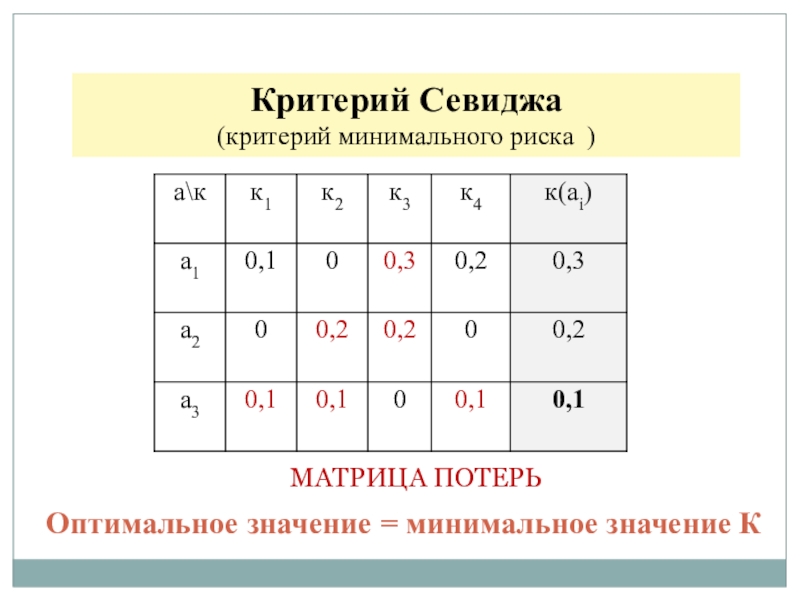
Слайд 16Критерий Севиджа
(критерий минимального риска )
МАТРИЦА ПОТЕРЬ
Оптимальное значение = минимальное
значение К
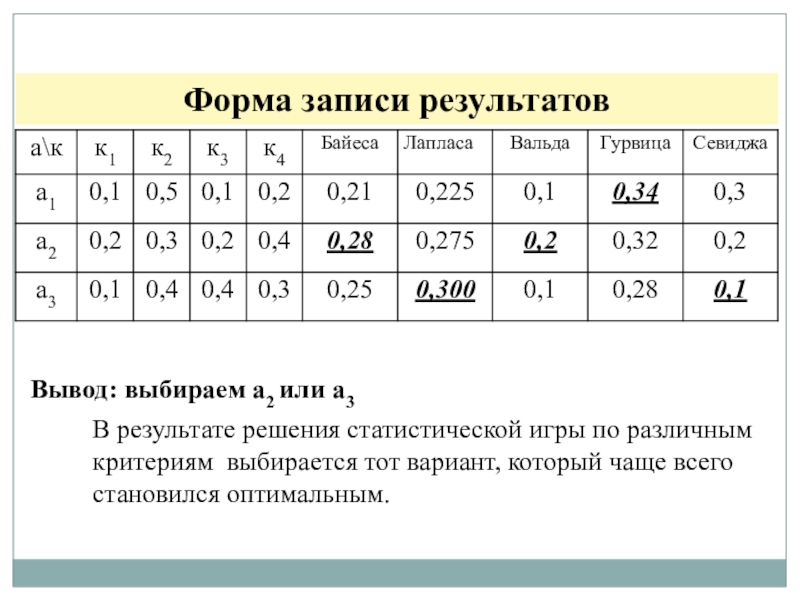
Слайд 17Форма записи результатов
Вывод: выбираем а2 или а3
В результате решения статистической
игры по различным критериям выбирается тот вариант, который чаще всего
становился оптимальным.
Слайд 18РЕШИТЕ ЗАДАЧУ
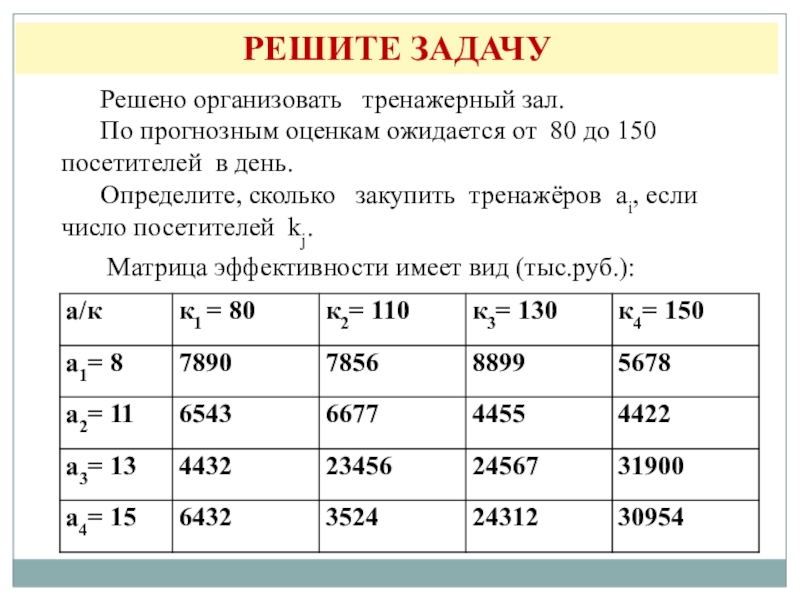
Решено организовать тренажерный зал.
По прогнозным оценкам ожидается
от 80 до 150 посетителей в день.
Определите, сколько
закупить тренажёров аi, если число посетителей kj.Матрица эффективности имеет вид (тыс.руб.):
