Слайд 1Теория субъективной полезности Неймана - Моргенштерна
Семинар № 4
Слайд 2Задача о двух банках
Коммерческий Гамма-банк рассматривает следующие две возможности вложения
средств.
Первая возможность связана с предложением ИТ-компании Big Brother, которая с
использованием технологии больших данных и машинного обучения разработала систему, позволяющую на основе анализа профилей в социальных сетях весьма достоверно предсказывать вероятность возврата физическими лицами краткосрочных кредитов, предоставляемых на стандартных условиях: срок кредита 1 год, сумма 100 тысяч рублей, ставка – 15%. Речь идет о системе, которая выдает решение о кредите практически мгновенно, что является дополнительным элементом маркетинга продукта. Подготовлена рекламная кампания под слоганом «Решение о кредите – три минуты, нужен только Ваш паспорт!». Тестовое использование системы показало, что вероятность возврата кредита, выданного с ее использованием, составляет 90%. Big Brother предлагает Гамма-банку возможность использования системы для выдачи 1000 кредитов (1000 положительных решений) за 1 миллион рублей. Расчеты – через год, после завершения кампании. Таким образом, первая возможность предполагает инвестирование 100 миллионов рублей в проект кредитования физических лиц под высокий процент при условии моментальной выдачи кредитов.
Вторая возможность вложения 100 миллионов рублей для Гамма-банка состоит в приобретении облигаций золотодобывающей компании с фиксированной доходностью 2,2% годовых. Аналитики банка рассматривают это вариант как фактически безрисковый, учитывая экономическое положение и историю золотодобывающей компании.

Слайд 3Задача о двух банках
На указанные облигации золотодобывающей компании с фиксированной
доходностью претендует также Тау-банк.
Однако для этого банка альтернативой вложения в
безрисковые облигации является вложение 100 миллионов рублей в проект мини-кофеен «Кофе за углом». Исходя из бизнес-модели, аналитики Тау-банка оценивают прибыльность проекта, если он, как говорят «полетит», то есть будет принят рынком, в 15% , но предупреждают, что с учетом высокой конкуренции на этом рынке (проекты Cofix и другие) есть 10% вероятность того, что проект потерпит крах.
Постройте деревья решений для Гамма- и Тау-банков и предложите, каким образом должны приниматься решения в обоих случаях и какое решение следует принять каждому из банков.
Слайд 4Сравнение стратегий управления риском
Если результат решения используется многократно, то в
качестве критерия сравнения альтернативных стратегий возможно применение показателей среднего эффекта
(средних ожидаемых затрат, выручки и т.п.). Критерий максимума EMV.
Если результат используется однократно, то применение критериев типа среднего эффекта бессмысленно и для выбора конкретной стратегии следует воспользоваться иными подходами.
Теория субъективной полезности Неймана-Моргенштерна. Критерий максимума ожидаемой полезности.
Слайд 5Почему так?
Если мы 1000 раз подбросим монету, сколько раз выпадет
орел?
Если подбросим монету 10 раз, то сколько раз выпадет орел?
Какая
теорема помогает дать ответ на эти вопросы?
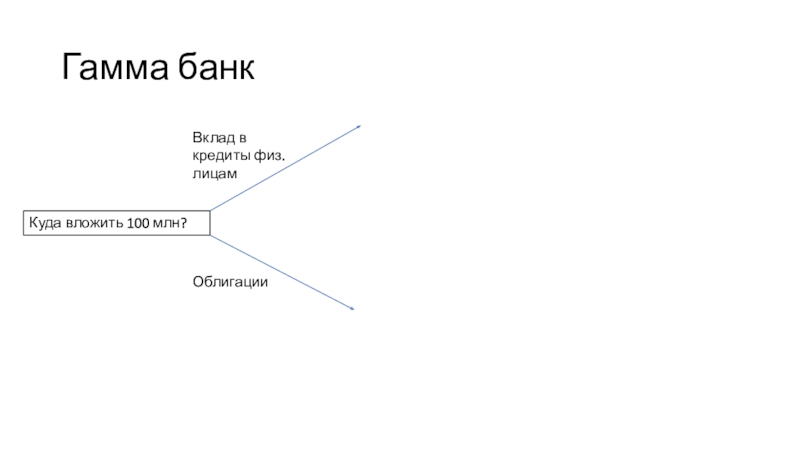
Слайд 7Гамма банк
Куда вложить 100 млн?
Вклад в кредиты физ.лицам
Облигации
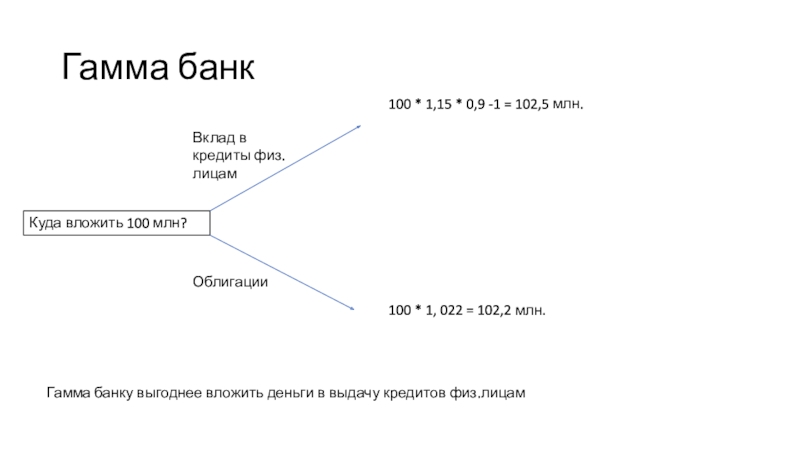
Слайд 8Гамма банк
Куда вложить 100 млн?
Вклад в кредиты физ.лицам
Облигации
100 * 1,15
* 0,9 -1 = 102,5 млн.
100 * 1, 022 =
102,2 млн.
Гамма банку выгоднее вложить деньги в выдачу кредитов физ.лицам
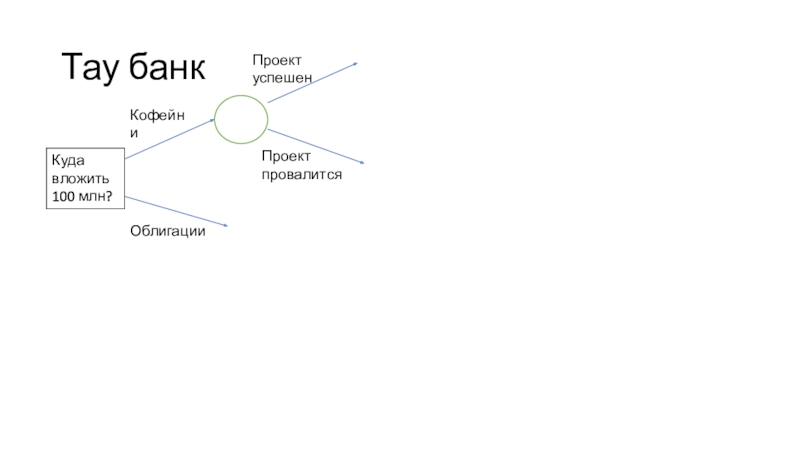
Слайд 9Тау банк
Куда вложить 100 млн?
Кофейни
Облигации
Проект успешен
Проект провалится
Слайд 10Тау банк
В данном случае нельзя считать мат.ожидание результата, т.к. событие
однократное. Вкладываем 100 млн в один проект, а не как
в предыдущем случае 100 млн в 1000 кредитов.
Нет объективно лучшего решения, объясняем с помощью функции полезности
Куда вложить 100 млн?
Кофейни
Облигации
102,2 млн
Проект успешен
Проект провалится
0 млн. p=0,1
100*1,15=115 млн. p=0,9
Слайд 11Тау банк
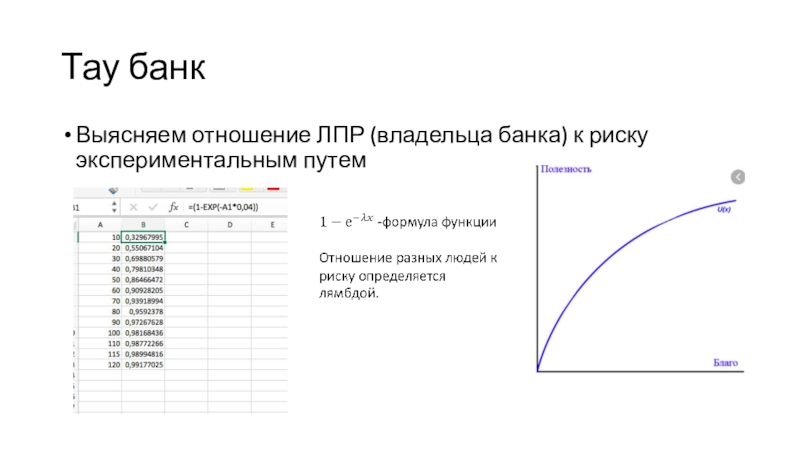
Выясняем отношение ЛПР (владельца банка) к риску экспериментальным путем
Слайд 12Тау банк
Выясняем отношение ЛПР (владельца банка) к риску экспериментальным путем
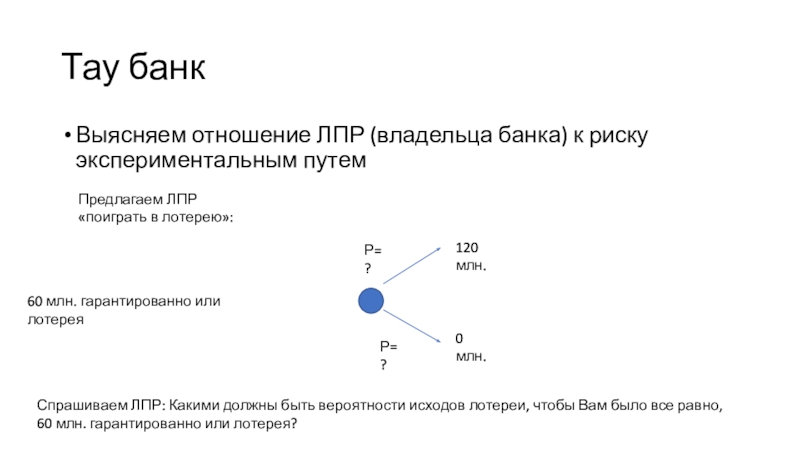
Предлагаем
ЛПР «поиграть в лотерею»:
60 млн. гарантированно или лотерея
0 млн.
120
млн.
Р=?
Р=?
Спрашиваем ЛПР: Какими должны быть вероятности исходов лотереи, чтобы Вам было все равно, 60 млн. гарантированно или лотерея?
Слайд 13Тау банк
Выясняем отношение ЛПР (владельца банка) к риску экспериментальным путем
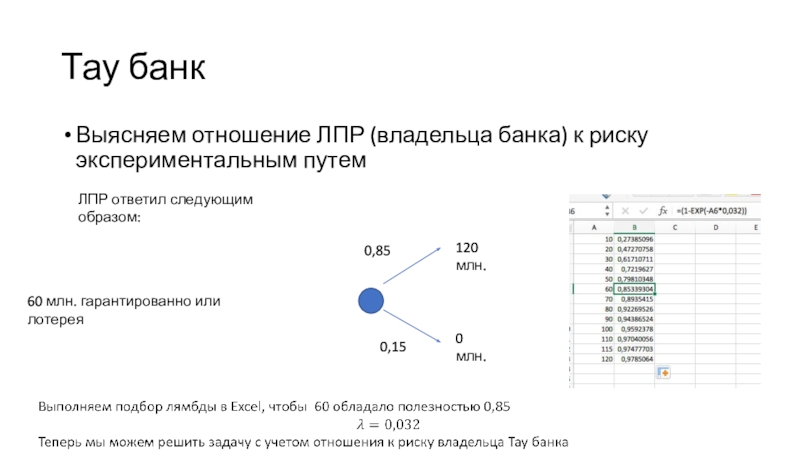
ЛПР
ответил следующим образом:
60 млн. гарантированно или лотерея
0 млн.
120 млн.
0,85
0,15
Слайд 14Тау банк
Считаем EU (expected utility) для каждой альтернативы:
EU для проекта
вложений в кофейни: 0,97*0,9+0*0,1 = 0,873
EU для облигаций: 0,96*1=0,96
Сравниваем ожидаемую
полезность, выбираем вклад в облигации
Куда вложить 100 млн?
Кофейни
Облигации
102,2 млн
Полезность u=0,96
Проект успешен
P=0,9
Проект провалится
P=0,1
0 млн.
Полезность u=0
100*1,15=115 млн.
Полезность u=0,97
Слайд 15Задача № 2
Лицо, принимающее решение, (ЛПР) рассматривает два варианта
вложения средств:
Первый вариант с вероятностью 60% принесет через год 110
денежных единиц, но с вероятностью 40% результат будет только 100 единиц.
Второй вариант с вероятностью 80% принесет 120 единиц, но с вероятностью 20% результат будет только 50.
Слайд 16Описывающее отношение к риску данного ЛПР функция полезности задана таблицей:
10
0,32967995
20 0,55067104
30 0,69880579
40 0,79810348
50 0,86466472
60 0,90928205
70 0,93918994
80 0,9592378
90 0,97267628
100 0,98168436
110
0,98772266
120 0,99177025
Слайд 17Вопросы
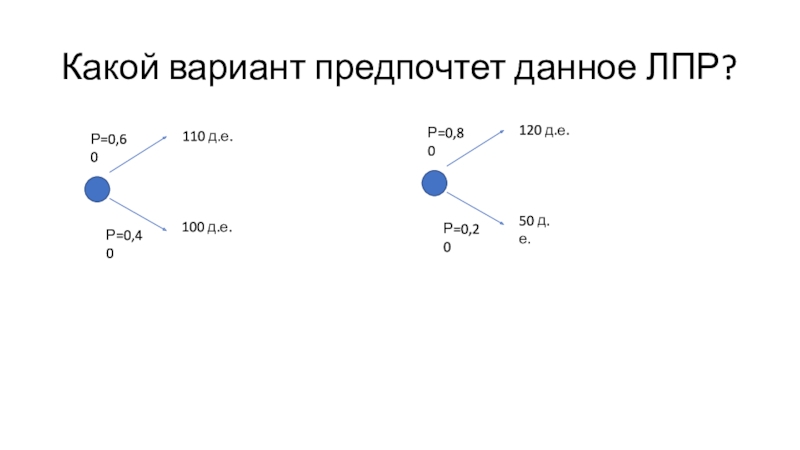
1. Какой вариант предпочтет данное ЛПР?
2. Какая денежная сумма является
детерминированным эквивалентом первого варианта вложений?
3. Данное ЛПР склонно, или несклонно
к риску? Может быть, оно нейтрально по отношению к риску? Поясните ответ.
4. Есть возможность модифицировать первый вариант вложений, увеличив максимально возможный результат в нем до 115 единиц. Но вероятность этого максимального результата будет при этом 0,55. (Соответственно, вероятность худшего исхода в 100 единиц будет 0,45). Оправданна ли такая модификация с точки зрения ЛПР?
5. Есть возможность модифицировать второй вариант, увеличив результат при менее благоприятном исходе с 50 до 60 единиц. Но за это придется заплатить 7 единиц (плата вносится заранее, независимо от того, каков будет исход проекта). Оправданна ли такая модификация с точки зрения ЛПР?
Примечание. При необходимости получить значения функции полезности для значений аргумента, отсутствующих в таблице, используйте линейную интерполяцию.
Слайд 18Какой вариант предпочтет данное ЛПР?
100 д.е.
110 д.е.
Р=0,60
Р=0,40
50 д.е.
120 д.е.
Р=0,80
Р=0,20
Слайд 19Какой вариант предпочтет данное ЛПР?
EU1 = 0,6* 0,98772266 +0,4* 0,98168436=
0,98530734
EU2 = 0,8* 0,99177025 +0,2* 0,86466472= 0,96634914
Выбираем вариант 1
100 д.е.
U=
0,98168436
110 д.е.
U= 0,98772266
Р=0,60
Р=0,40
50 д.е.
U= 0,86466472
120 д.е.
U= 0,99177025
Р=0,80
Р=0,20
Слайд 20Какая денежная сумма является детерминированным эквивалентом первого варианта вложений?
Нужно найти
деньги, эквивалентные EU1= 0,98530734
Линейная интерполяция
Ответ: 106
Слайд 21Данное ЛПР склонно, или несклонно к риску? Может быть, оно
нейтрально по отношению к риску? Поясните ответ.
Ответ: не склонно к
риску
Слайд 22Вопрос 4
U для 115= 0,98958065
Рассчитаем EU для модифицированного варианта
Слайд 23Вопрос 4
EU1старое = 0,6* 0,98772266 +0,4* 0,98168436= 0,98530734
EU1новое =
0,55* 0,98958065 +0,45* 0,98168436 = 0,98602727
EU1новое > EU1старое, модификация оправдана
100
д.е.
U= 0,98168436
115 д.е.
U= 0,98958065
Р=0,55
Р=0,45
Слайд 24Вопрос 5
EU2старое = 0,8* 0,99177025 +0,2* 0,86466472= 0,96634914
Есть возможность модифицировать
второй вариант, увеличив результат при менее благоприятном исходе с 50
до 60 единиц. Но за это придется заплатить 7 единиц (плата вносится заранее, независимо от того, каков будет исход проекта). Оправданна ли такая модификация с точки зрения ЛПР?
50 д.е.
U= 0,86466472
120 д.е.
U= 0,99177025
Р=0,80
Р=0,20
60 д.е. – 7 д.е. =53 д.е.
U= ?
120 д.е. – 7 д.е. = 113 д.е.
U= ?
Р=0,80
Р=0,20
Слайд 25Вопрос 5
Ищем значения полезности для исходов 113 и 53 с
помощью линейной интерполяции в Excel
Слайд 26Вопрос 5
EU2старое = 0,8* 0,99177025 +0,2* 0,86466472= 0,96634914
EU2новое = 0,8*
0,98857197 +0,2* 0,87804992 = 0,96646756
Модификация оправдана
50 д.е.
U= 0,86466472
120 д.е.
U= 0,99177025
Р=0,80
Р=0,20
60
д.е. – 7 д.е. =53 д.е.
U= 0,87804992
120 д.е. – 7 д.е. = 113 д.е.
U= 0,98857197
Р=0,80
Р=0,20