Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория вероятностей
Содержание
- 1. Теория вероятностей
- 2. Замечательно, что наука, которая началась с рассмотрения
- 3. Теория вероятностей Теория вероятностей
- 4. Событие Событие - это явление,
- 5. Испытание Испытания - это условия,
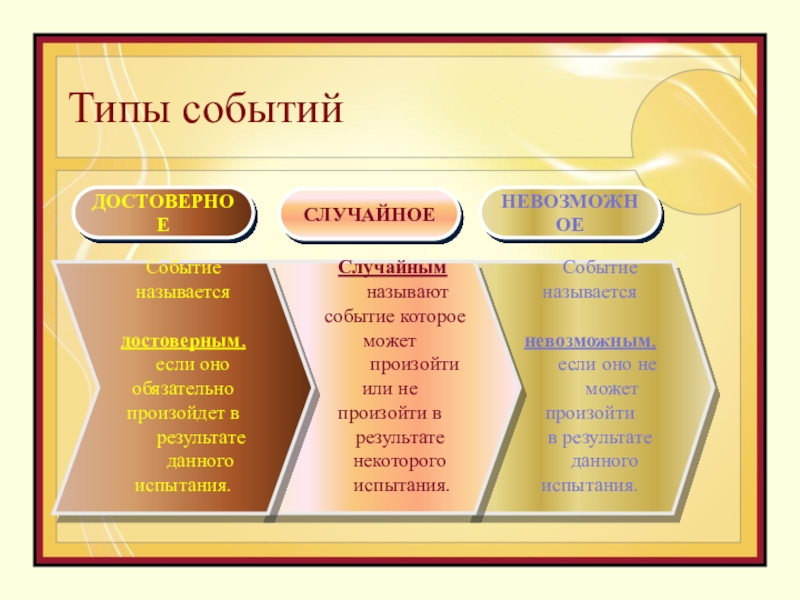
- 6. Типы событий Событие называется
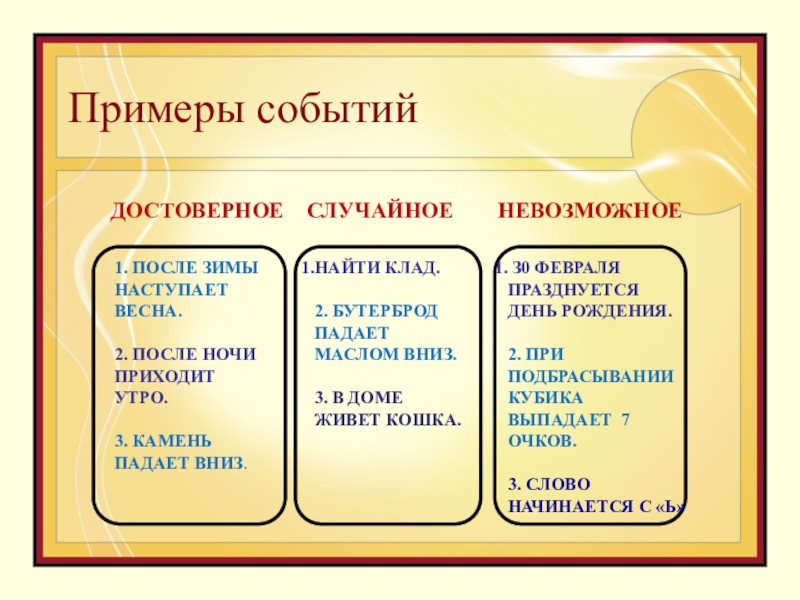
- 7. Примеры событий1. ПОСЛЕ ЗИМЫ НАСТУПАЕТ ВЕСНА.2. ПОСЛЕ
- 8. Охарактеризуйте события, о которых идет
- 9. Устное задание2В мешках лежит 10 шаров: 3
- 10. Полная группаПолной группой событий называется множество таких
- 11. Попарно несовместимые событияПопарно несовместимые события - это события, два из которых не могут происходить одновременно.
- 12. Равновозможные событияРавновозможные события - это такие события,
- 13. Пространство элементарных событийСобытия, образующие полную группу событий, являющиеся несовместимыми и равновозможными, образуют пространство элементарных событий.
- 14. Испытания с монетой Французский естествоиспытатель Бюффон бросал
- 15. Испытания с монетой Английский математик Карл Пирсон
- 16. Классическое определение вероятностиПьер Симон Лаплас (1749-1827)Отношение числа
- 17. Формула вероятностиР - от первой буквы французского
- 18. Пример. Подбрасываем две одинаковые монеты. Какова вероятность
- 19. Ошибка Даламбера. Великий французский философ
- 20. Использованные источникиЯ. Перельман. Занимательная геометрия на вольном
- 21. Скачать презентанцию
Замечательно, что наука, которая началась с рассмотрения азартных игр, обещает стать наиболее важным объектом человеческого знания... Ведь по большей части важнейшие жизненные вопросы являются на самом деле лишь задачами теории вероятностей
Слайды и текст этой презентации
Слайд 3Теория вероятностей
Теория вероятностей - раздел математики,
изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства
и операции над ними.
Слайд 4Событие
Событие - это явление, о котором можно
сказать, что оно происходит или не происходит при определенных условиях.
Слайд 5Испытание
Испытания - это условия, в результате которых
происходит или не происходит событие.
Например:
Испытание -
подбрасывание монеты События: А – {появление герба}, В – {появление решки}
Слайд 6Типы событий
Событие называется
невозможным,
если оно не
может произойтив результате
данного испытания.
Случайным
называют
событие которое может
произойти или не произойти в
результате
некоторого
испытания.
Событие
называется
достоверным,
если оно обязательно произойдет в
результате
данного испытания.
ДОСТОВЕРНОЕ
СЛУЧАЙНОЕ
НЕВОЗМОЖНОЕ
Слайд 7Примеры событий
1. ПОСЛЕ ЗИМЫ НАСТУПАЕТ ВЕСНА.
2. ПОСЛЕ НОЧИ ПРИХОДИТ УТРО.
3.
КАМЕНЬ ПАДАЕТ ВНИЗ.
НАЙТИ КЛАД.
2. БУТЕРБРОД ПАДАЕТ МАСЛОМ ВНИЗ.
3. В ДОМЕ
ЖИВЕТ КОШКА. З0 ФЕВРАЛЯ
ПРАЗДНУЕТСЯ
ДЕНЬ РОЖДЕНИЯ.
2. ПРИ ПОДБРАСЫВАНИИ КУБИКА ВЫПАДАЕТ 7 ОЧКОВ.
3. СЛОВО НАЧИНАЕТСЯ С «Ь»
ДОСТОВЕРНОЕ СЛУЧАЙНОЕ НЕВОЗМОЖНОЕ
Слайд 8 Охарактеризуйте события, о которых идет речь в приведенных заданиях как
достоверные, невозможные или случайные.
1
Задумано натуральное число. Событие состоит в следующем:
а)
задумано четное число;б) задумано нечетное число;
в) задумано число, не являющееся ни четным, ни нечетным;
г) задумано число, являющееся четным или нечетным.
Слайд 9Устное задание
2
В мешках лежит 10 шаров: 3 синих, 3 белых
и 4 красных. Охарактеризуйте следующее событие:
а) из мешка вынули 4
шара и они все синие;б) из мешка вынули 4 шара и они все красные;
в) из мешка вынули 4 шара, и все они оказались разного цвета;
г) из мешка вынули 4 шара, и среди них не оказалось шара черного цвета.
Слайд 10Полная группа
Полной группой событий называется множество таких событий, что в
результате каждого испытания обязательно должно произойти хотя бы одно из
них.
Слайд 11Попарно несовместимые события
Попарно несовместимые события - это события, два из
которых не могут происходить одновременно.
Слайд 12Равновозможные события
Равновозможные события - это такие события, каждое из которых
не имеет никаких преимуществ в появлении чаще других во время
многократных испытаний, проводимых при одинаковых условиях.
Слайд 13Пространство элементарных событий
События, образующие полную группу событий, являющиеся несовместимыми и
равновозможными, образуют пространство элементарных событий.
Слайд 14Испытания с монетой
Французский естествоиспытатель Бюффон бросал монету 4040 раз, и
при этом герб выпал в 2048 случаях.
Жорж Бюффон
(1707-1788)
Слайд 15Испытания с монетой
Английский математик Карл Пирсон бросал монету 24000 раз
- герб выпал 12012 раз.
Карл Пирсон
(1857-1936)
Слайд 16Классическое определение вероятности
Пьер Симон Лаплас
(1749-1827)
Отношение числа событий, благоприятствующих появлению
события А, к общему числу событий пространства, называют вероятностью события
А и обозначают Р(А).
Слайд 17Формула вероятности
Р - от первой буквы французского слова probabilite –
вероятность.
m – количество благоприятных событий
n – общее число событий пространства
Слайд 18Пример. Подбрасываем две одинаковые монеты. Какова вероятность того, что они
упадут на одну и ту же сторону?
Решение № 1.
Опыт имеет
триравновозможных исхода:
1) обе монеты упадут на «орла»;
2) обе монеты упадут на «решку»;
3) одна из монет упадет на «орла», другая на «решку».
Из них благоприятными
будут два исхода.
Решение № 2.
Опыт имеет четыре
равновозможных исхода:
1) обе монеты упадут на «орла»;
2) обе монеты упадут на «решку»;
3) первая монета упадет на «орла», вторая на «решку»;
4) первая монета упадет на «решку», вторая на «орла».
Из них благоприятными будут
два исхода.
Слайд 19Ошибка Даламбера.
Великий французский философ и математик Даламбер
вошел в историю теории вероятностей со своей знаменитой ошибкой, суть
которой в том, что он неверно определил равновозможность исходов в опыте всего с двумя монетами!Жан Лерон Даламбер
(1717 -1783)
Слайд 20Использованные источники
Я. Перельман. Занимательная геометрия на вольном воздухе и дома.
- М, 2012.
2. Башмаков, М.И. Математика: учебник для учреждений нач. и
сред. проф. образования / М.И.Башмаков – 8-е изд., стер. - М.: Академия, 2013.-256 c.3. Математика. 10-11 классы: элективный курс «В мире случайных закономерностей» / ав.-сост. В.Н. Студенецкая и др. – Волгоград: Учитель, 2007. – 126 с.
