Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория вероятностей
Содержание
- 1. Теория вероятностей
- 2. Немного историиИсторически теория вероятностей возникла как теория
- 3. Комбинаторика
- 4. Немного истории Элементы теории комбинаторики были известны
- 5. Немного истории Название «перестановка» впервые употребил
- 6. Правило суммы: Если элемент А может
- 7. Правило произведения: Если элемент А может
- 8. Схема выбора, приводящая к сочетаниям
- 9. Задача 1: Сколькими способами из колоды в 52 карты можно вынуть 10 карт?
- 10. Задача 2: У англичан принято
- 11. Задача 3: Хоккейная
- 12. Схема выбора, приводящая к размещениям Если
- 13. Задача 1:В президиум выбрано 10 человек.
- 14. Задача 2:Номер кодового замка состоит из
- 15. Задача 2: Автомобильные номера состоят
- 16. Схема выбора, приводящая к перестановкам Частным
- 17. Примеры:Сколько различных перестановок можно образовать из букв
- 18.
- 19. Сочетания с повторами:
- 20. Размещения с повторами:
- 21. Перестановки с повторами:
- 22. Элементарным исходом (событием) называют любой простейший
- 23. Иначе, множество исходов образует пространство элементарных событий,
- 24. Классификация событий: Событие А называется случайным
- 25. СобытияСобытия: 1) наступила весна 2) наступила осень 3) на
- 26. Проверка Совместные1) и 3) 1) и 4)1) и
- 27. Классификация событий: Событие А называется достоверным
- 28. Задания.Бросается октаэдр, у которого одна грань зеленая,
- 29. СобытияРавновозможные - те, в наступлении одного из
- 30. Событиеневозможное
- 31. Событиелюбое явление, которое происходит или не происходитпример:
- 32. Задания. Для каждого из событий определить, каким
- 33. Действия над событиями: Произведением (пересечением) двух
- 34. Действия над событиями: Суммой (объединением)двух событий
- 35. Действия над событиями: Событием противоположным по отношению
- 36. Действия над событиями: Справедливо
- 37. Примеры:Из таблицы случайных чисел наудачу взято одно
- 38. Немного истории Впервые вероятность случайных событий
- 39. Говорят, что события
- 40. Классическое определение вероятности: Пусть некоторый опыт допускает
- 41. Классическое определение вероятности:Так как Если
- 42. Задача 1: Из колоды в 36 карт,
- 43. Задача 2: Код домофона состоит из 8
- 44. Задача 3: 10 человек случайным образом рассаживаются
- 45. Задача 4: Бросаются две игральные кости. Найти
- 46. Задача 5: Какова вероятность того, что наудачу
- 47. Геометрическое определение вероятности: Вероятностью события А
- 48. Задача 1: Два
- 49. Задача 2:На плоскости начерчены
- 50. Определение: События А и В называются
- 51. Теорема умножения вероятностей:Для независимых событий:Для зависимых событий:
- 52. Задача 1: Слово ’’
- 53. Задача 2: Вероятность того, что
- 54. Задача 3: Вероятность
- 55. Теорема сложения вероятностейДля несовместных событий:Для совместных событий:
- 56. Задача 1: Три
- 57. Задача 2:В кошельке лежат
- 58. Слайд 58
- 59. Задача 4: Два
- 60. Формула полной вероятности Пусть событие
- 61. Формула Байеса:
- 62. Задача 1:Стрельба производится
- 63. Слайд 63
- 64. Задача
- 65. Задача 4: Вероятности
- 66. Спасибо за внимание!!!
- 67. Скачать презентанцию
Немного историиИсторически теория вероятностей возникла как теория азартных игр (рулетка, игральные кости, карты и т.д.) в конце XVII в. Начало ее развития связано с именами Б.Паскаля, Я. Бернулли, А. Муавра, П.
Слайды и текст этой презентации
Слайд 1Теория вероятностей
Замечательно, что науке, начинавшейся с рассмотрения азартных игр, суждено
было стать важнейшим объектом человеческого знания…
Слайд 2Немного истории
Исторически теория вероятностей возникла как теория азартных игр (рулетка,
игральные кости, карты и т.д.) в конце XVII в. Начало
ее развития связано с именами Б.Паскаля, Я. Бернулли, А. Муавра, П. Лапласа, а позднее – К. Гаусса, С. Пуассона.Первыми источниками по теории вероятности являются сочинения Гюйгенса «De ratioliniis in ludo aleae» («О расчете в азартных играх») и посмертное произведение Я.Бернулли «Ars conjenctandi» («Искусство предположений»).
Первые исследования по теории вероятностей в России относятся к середине XIX в., и связаны с такими именами, как, Н.И. Лобачевский, М.В. Остроградский, В.Я. Буняковский.
Слайд 4Немного истории
Элементы теории комбинаторики были известны еще в древности.
К XVII в. были накоплены многочисленные результаты Тартальи, Эригона, Паскаля,
Ферма. Однако научное основание теории дал двадцатилетний Лейбниц в труде «Dissertatio de art combinatoria» («Рассуждение о комбинаторном искусстве»).Термин «сочетание» (Combination) впервые употребил Паскаль. Формула для сочетаний была известна Тарталье, хотя независимо от него формулу нашел Эригон. Обозначение С по первой букве латинского названия введено в 1880г.
Слайд 5Немного истории
Название «перестановка» впервые употребил Таке в «Теории
и практике арифметики», это наименование осталось в математике благодаря тому,
что его принял Я. Бернулли. Обозначение P происходит от слова permutation – «перестановка»- введено Поттсом.Слово «размещение» встречается у Я.Бернулли, правда только один раз и в виде «сочетание вместе с перестановками». Обозначение размещения через А – от – arrangement – появилось впервые в 1904г. В статье Нетто.
Слайд 6Правило суммы:
Если элемент А может быть выбран m
способами, а элемент В n способами, то выбор «А или
В» может быть осуществлен способами.Пример: Пусть в корзине имеется 7 апельсинов,5 бананов и 10 яблок. Сколькими способами можно выбрать один фрукт?
Ответ: 7+5+10=22
Слайд 7Правило произведения:
Если элемент А может быть выбран m
способами и после такого выбора, элемент В может быть выбран
n способами, то выбор «А и В» может быть осуществленm . n способами.
Пример: В спортивном велосипеде имеются 3 ведущие и 4 ведомые звездочки. Сколько передач имеется в велосипеде?
Ответ:4*3=12
Слайд 8Схема выбора, приводящая к сочетаниям
Если опыт состоит
в выборе элементов без возвращения и без упорядочивания из данных
, то получаемые при этом комбинации (неупорядоченные наборы) носят название сочетания без повторений из n элементов по k. Множество таких сочетаний обозначается:
Слайд 10 Задача 2: У англичан принято давать детям несколько имён. Сколькими
способами можно назвать ребёнка, если общее число имён 300, а
ему дают не более трёх?
Слайд 11 Задача 3: Хоккейная команда состоит из 2 вратарей , 7
защитников и 10 нападающих. Сколькими способами тренер может образовать стартовую
шестёрку, состоящую из вратаря, 2 защитников и 3 нападающих?
Слайд 12Схема выбора, приводящая к размещениям
Если опыт состоит в
выборе элементов без возвращения, но с упорядочиванием их по мере
выбора в последовательную цепочку, то полученные при этом упорядоченные комбинации, отличающиеся либо набором элементов, либо порядком их следования, называются размещениями без повторений из n элементов по k и обозначаются:
Слайд 13 Задача 1:В президиум выбрано 10 человек. Сколькими способами из них
можно выбрать председателя и секретаря?
Слайд 14 Задача 2:Номер кодового замка состоит из двух букв и четырех
цифр. Сколько различных номеров можно составить, используя 30 букв и
10 цифр?
Слайд 15 Задача 2: Автомобильные номера состоят из 1 , 2 или
3 букв и 4 цифр. Найти число таких номеров, где
используется 32 буквы русского алфавита (элементы не повторяются).
Слайд 16Схема выбора, приводящая к перестановкам
Частным случаем размещений без
повторений, когда n=k, являются комбинации, называемые перестановками без повторений. В
этом случае опыт состоит в произвольном упорядочивании, т.е. сводится к случайной перестановке элементов. Обозначаются:
Слайд 17Примеры:
Сколько различных перестановок можно образовать из букв слова "зебра"?
Сколькими
различными способами можно расставить 6 человек в очереди?
Сколько ожерелий
можно составить из 7 различных бусин ? 
Слайд 22 Элементарным исходом (событием) называют любой простейший (т.е. неделимый в
рамках данного опыта) исход опыта.
Множество всех элементарных исходов называется
пространством элементарных событий и обозначается Определение:
Слайд 23Иначе, множество исходов образует пространство элементарных событий, если выполнены следующие
требования:
в результате опыта одно из событий обязательно происходит;
появление одного
из событий исключает появление остальных;в рамках данного опыта нельзя разделить элементарный исход на более мелкие составляющие.
Слайд 24Классификация событий:
Событие А называется случайным по отношению к
данному опыту, если в результате опыта оно может произойти, а
может не произойти.Событие А называется невозможным по отношению к данному опыту, если оно не произойдет в результате данного опыта.
Слайд 25События
События:
1) наступила весна 2) наступила осень 3) на небе солнце 4) подул
ветер
5) на небе месяц 6) пошел дождь 7) листопад
Совместные – два события,
которые в данных условиях могут происходить одновременно.Несовместные – те, которые не могут происходить одновременно.
Слайд 26Проверка
Совместные
1) и 3) 1) и 4)
1) и 5) 1) и 6)
2) и
3) 2) и 4)
2) и 6) 2) и 7)
3) и 4) 3) и
7)4) и 5) 4) и 6)
4) и 7) 5) и 7)
6) и 7) 3) и 6)
Несовместные
1) и 2)
3) и 5)
1) и 7)
наступила весна 2) наступила осень 3) на небе солнце
4) подул ветер 5) на небе месяц 6) пошел дождь 7) листопад
Слайд 27Классификация событий:
Событие А называется достоверным по отношению к
данному опыту, если оно обязательно произойдет в результате данного опыта.
События А и В называются несовместными по отношению к данному опыту, если они не могут произойти одновременно.События А и В называются равновозможными или равновероятными по отношению к данному опыту, если объективно ни одно из них не является более возможным, чем другое по отношению к данному опыту.
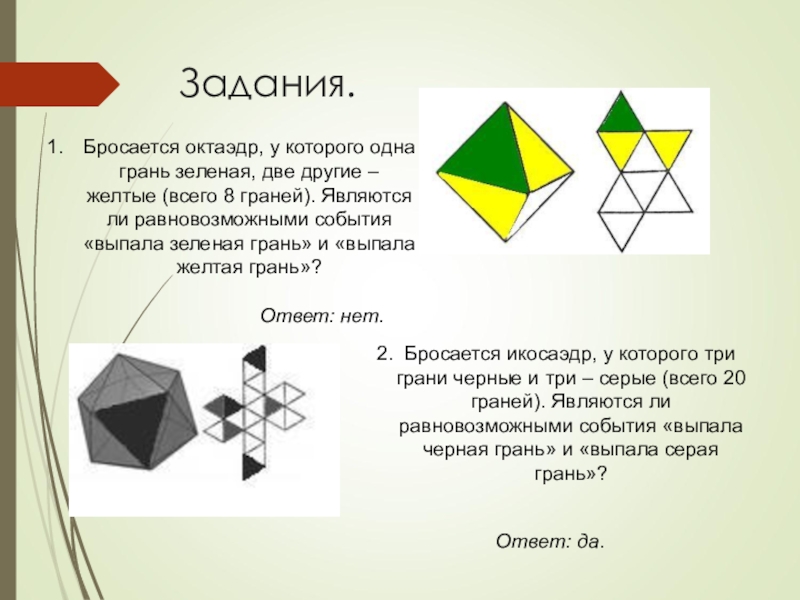
Слайд 28Задания.
Бросается октаэдр, у которого одна грань зеленая, две другие –
желтые (всего 8 граней). Являются ли равновозможными события «выпала зеленая
грань» и «выпала желтая грань»?2. Бросается икосаэдр, у которого три грани черные и три – серые (всего 20 граней). Являются ли равновозможными события «выпала черная грань» и «выпала серая грань»?
Ответ: нет.
Ответ: да.
Слайд 29События
Равновозможные - те, в наступлении одного из которых нет никакого
преимущества.
Примеры:
1) появление определенного количества очков при бросании игрального кубика
2) «приземление»
тетраэдра на одну из граней Неравновозможные – те, в наступлении одного из которых есть какое-то преимущество.
Примеры:
1) вытащили дубль (в наборе домино 28 костяшек, дублей в наборе – 7):
2) куб «упал на желтую грань» и куб «упал на синюю грань»
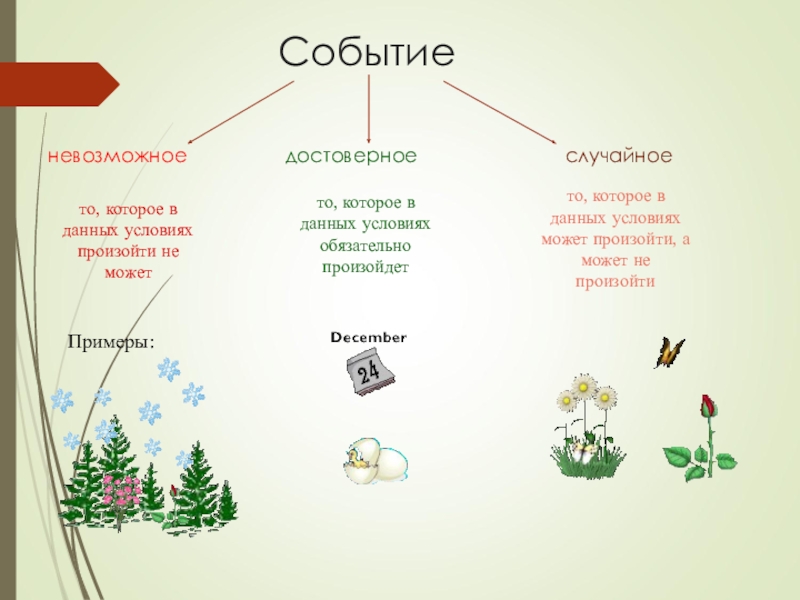
Слайд 30Событие
невозможное достоверное
случайное
то, которое в данных условиях произойти
не можетто, которое в данных условиях обязательно произойдет
то, которое в данных условиях может произойти, а может не произойти
Примеры:
Слайд 31Событие
любое явление, которое происходит или не происходит
пример: изменение погоды
результаты испытаний
(опытов), наблюдений и измерений, производимых людьми
пример: измерение температуры воздуха ,наблюдение
за полетом бабочки
Слайд 32Задания.
Для каждого из событий определить, каким оно является:
Невозможное
Достоверное
Случайное
2 июля в
Санкт-Петербурге будет гроза;
после 3 урока будет 4 урок;
ребенок в 1
год поступает в институт;зимой выпадает снег;
при включении компьютера, вентилятор сломается;
вы плаваете в реке, а на встречу вам плывет акула
Слайд 33Действия над событиями:
Произведением (пересечением) двух событий А и
В называют событие С, происходящее тогда и только тогда, когда
одновременно происходят оба события, т.е событие состоящее из тех и только тех элементарных исходов, которые принадлежат и событию А и событию В Обозначается С=А . В.
Слайд 34Действия над событиями:
Суммой (объединением)двух событий A и В
называют событие С, происходящее тогда и только тогда, когда происходит
хотя бы одно из событий А или В (т.е состоящее из тех элементарных исходов, которые принадлежат хотя бы одному из подмножеств А или В): С=А+В
Слайд 35Действия над событиями:
Событием противоположным по отношению к событию А,
называют событие , происходящее тогда и только тогда, когда
не происходит событие А.Пример: А – из трех проверяемых изделий, все доброкачественные.
Слайд 36Действия над событиями:
Справедливо равенство
где - достоверное событие,
а
, – недостоверное событие
Слайд 37Примеры:
Из таблицы случайных чисел наудачу взято одно число. Событие А
— выбранное число делится на 5; Событие В — это
число оканчивается нулем. Что означают события А + В, А · В, , ?Два шахматиста играют одну партию. Событие А — выигрывает первый игрок, В — второй игрок. Какое событие следует добавить к указанной совокупности, чтобы получилась полная группа событий? Что означают события А + В, А · В ?
Слайд 38Немного истории
Впервые вероятность случайных событий в азартных
играх вычислили в 18в.французские математики Блез Паскаль и Пьер Ферма.
Они подсчитывали число шансов события из общего возможного числа равновероятных исходов.Первое определение вероятности дал Я.Бернулли: вероятность есть «степень уверенности и относится к достоверности, как часть к целому».
Так называемое классическое определение вероятности было сформулировано в курсе лекций, которые читал Лаплас в 1795г. Он писал: «Теория вероятностей есть, собственно говоря, только переложение здравого смысла на формулы, она доставляет средства для точной оценки того, что постигает ум верный, хотя часто бессознательно».
Слайд 39 Говорят, что события
образуют полную группу
событий по отношению к данному опыту, если в результате опыта обязательно произойдет хотя бы одно из этих событий.Пусть это несовместные равновозможные события, образующие полную группу событий. Тогда эти события называются элементарными событиями (случаи, шансы).
Опыт, допускающий полную группу попарно несовместный событий, называется схемой случаев или схемой урн.
Говорят что событие благоприятствует событию А, если событие влечет за собой выполнение события А.
Слайд 40Классическое определение вероятности:
Пусть некоторый опыт допускает схему случаев. Пусть
число всех элементарных событий равно n , а событию А
благоприятствует m событий. Вероятностью события А называется число, равное отношению числа благоприятных исходов, к числу всевозможных
Слайд 41Классическое определение вероятности:
Так как
Если событие достоверное, то
его вероятность равна 1, если событие невозможное , то его
вероятность равна 0.
Слайд 42
Задача 1: Из колоды в 36 карт, наудачу вынимают три
карты. Найти вероятность того, что среди вынутых карт будет один
туз.
Слайд 43Задача 2: Код домофона состоит из 8 цифр, которые могут
повторяться. Какова вероятность того, что, случайно набирая цифры, можно угадать
нужный код?
Слайд 44Задача 3: 10 человек случайным образом рассаживаются на десятиместную скамейку.
Какова вероятность того, что два определенных лица окажутся рядом?
Слайд 45Задача 4: Бросаются две игральные кости. Найти вероятность того, что
сумма выпавших очков на обеих костях равна 4.
Слайд 46Задача 5: Какова вероятность того, что наудачу выбранное шестизначное число
составлено только из четных цифр? Известно, что число не содержит
цифры 0.
Слайд 47Геометрическое определение вероятности:
Вероятностью события А называется число, равное
отношению меры множества А, к мере множества
:
Слайд 48 Задача 1: Два человека договорились о встрече в определенном месте
в промежутке времени от 19.00 до 19.45. Каждый из них
приходит наудачу, независимо от другого и ожидает 15 минут. Какова вероятность того, что они встретятся?
Слайд 49 Задача 2:На плоскости начерчены две окружности, радиусы которых 5см. и
10 см. Найти вероятность того, что точка брошенная наудачу в
большой круг, попадет также в кольцо, образованное окружностями.
Слайд 50Определение:
События А и В называются независимыми, если появление
одного из них не меняет вероятность появления другого.
Вероятность
события А, вычисленную в предположении, что событие В произошло, называется условной вероятностью и обозначается:
Слайд 52 Задача 1: Слово ’’ реклама ’’ разрезано на отдельные буквы,
они перемешаны. Выбираются одна за другой три буквы. Какова вероятность,
что получиться слово “ мак “.
Слайд 53 Задача 2: Вероятность того, что в течение дня не произойдет
вызова спецназа, равна 0,03 . Какова вероятность того, что в
течение четырех дней подряд не произойдет ни одного вызова?
Слайд 54 Задача 3: Вероятность того, что студент 4-го курса перейдет на
5-ый равна 0,9. Вероятность окончить институт равна 0,7. Какова вероятность
того, что студент перейдет на 5-ый курс и окончит институт?
Слайд 56 Задача 1: Три стрелка стреляют по мишени. Вероятность попадания в
цель для первого стрелка равна 0,4; для второго — 0,5
и для третьего — 0,7. Найти вероятность того, что в результате однократного выстрела трех стрелков по мишени в ней будет ровно одна пробоина.
Слайд 57 Задача 2:В кошельке лежат три монеты достоинством по 10 копеек
и 7 монет пятикопеечных. Наудачу вынимаются две монеты. Какова вероятность
того, что обе монеты будут одного достоинства ?
Слайд 58 Задача 3: Симпатичная студентка Люся к зачету успела выучить только
10 вопросов из 20, но надеется, что в случае неудачи
уговорит профессора Евгения Васильевича задать ей второй вопрос. По многолетним наблюдениям профессора можно разжалобить в двух случаях из трех, и это соотношение не меняется с годами. Каковы Люсины шансы сдать зачет?
Слайд 59 Задача 4: Два баскетболиста попадают в сетку с вероятностями 0.8
и 0.7 соответственно. Каждый из них бросил по одному разу
мяч. Какова вероятность того, что: а) попал один из них, б) попал в корзину хотя бы один из них?
Слайд 60Формула полной вероятности
Пусть событие А может произойти
одновременно с одним из подсобытий
образующих полную группу событий, тогда
Слайд 62 Задача 1:Стрельба производится по пяти мишеням типа А, трем –
типа В и двум – типа С. Вероятности попадания в
мишени типа А, В, С, равны 0.4, 0.1, 0.15 соответственно. Найти вероятность поражения цели при одном выстреле, если неизвестно, в мишень какого типа он будет сделан.
Слайд 63 Задача 2: Два штрафника в наряде чистят картошку на кухне.
Более опытный из них обрабатывает в среднем 60% картофеля из
полученного объема. Вероятность того, что он допустит брак при чистке одной картофелины равна 0,05, а для менее опытного эта вероятность равна 0,1 . Взятая на контроль картофелина оказалась плохо очищенной. Какова вероятность того, что брак допущен более опытным штрафником?
Слайд 64 Задача 3:В специализированную больницу поступают в среднем 50% больных с
заболеванием К, 30% - с заболеванием М, 20% - с
заболеванием Л. Вероятности полного излечения болезней К, Л, М равны соответственно 0.7, 0.9, 0.8. Больной, поступивший в больницу, через некоторое время был выписан здоровым. Каким заболеванием вероятнее всего страдал больной?
Слайд 65 Задача 4: Вероятности того, что во время работы ЭВМ возникнет
сбой в АУ, ОЗУ и остальных устройствах, относятся как 3:2:5.
Вероятность обнаружить сбой в АУ, ОЗУ, остальных устройствах соответственно равна 0.8, 0.9, 0.9. Какова вероятность того, что возникший сбой в ЭВМ будет обнаружен?
