уравнения (1)
теплопроводности: .
В частном случае, для стационарного процесса ;при отсутствии внутренних источников теплоты
из (1) при следует:
или развернутое выражение
оператора Лапласа: . (2)
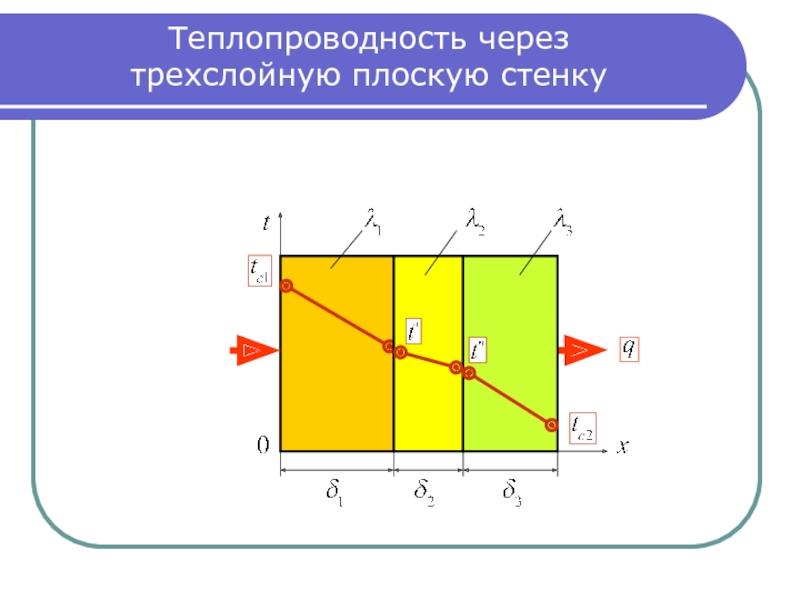
Для бесконечной пластины: , то есть:
.
Дифференциальное уравнение
теплопроводности запишется в виде: . (3)