Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Термодинамика и статистическая физика
Содержание
- 1. Термодинамика и статистическая физика
- 2. Лекция № 9Закон распределения Больцмана.1. Система
- 3. В отсутствие внешних сил средняя
- 4. концентрация молекул газа убывала с увеличением высоты.
- 5. Слайд 5
- 6. Вес столба n mg dZ S
- 7. Физическая природа силового поля не имеет
- 8. закон распределения БольцманаЗакон распределения частиц по
- 9. Слайд 9
- 10. Слайд 10
- 11. Пусть идеальный газ находится в поле консервативных
- 12. Слайд 12
- 13. С уменьшением температуры число молекул на
- 14. Распределение Больцмана можно предста-вить в виде
- 15. Опытное определение постоянной Авогадро. Ж. Перрен воспользовался
- 16. Если и
- 17. Слайд 17
- 18. Атмосфера Земли
- 19. Слайд 19
- 20. Вспомним строение атмосферы
- 21. Закон распределения Максвелла-Больцмана На прошлой
- 22. Закон Максвелла даёт распределение частиц по
- 23. Обозначим
- 24. В последнем выражении, потенциальная и кинетическая
- 25. где Ni – число частиц, находящихся в
- 26. Тогда, окончательное выражение распределения Масвелла-Больцмана для случая
- 27. Барометрическая формула Атмосферное
- 28. – плотность газа на высоте hгде С
- 29. Причём
- 30. Из барометрической формулы следует, что
- 31. Таким образом, чем тяжелее газ (> μ) и чем ниже температура, тем быстрее убывает давление.
- 32. Слайд 32
- 33. Распределение Бозе-Эйнштейна и Ферми-Дирака
- 34. Основная задача квантовой статистики состоит в
- 35. распределение Бозе-Эйнштейна:
- 36. Первая формула описывает квантовые частицы с целым
- 37. Лекция закончена !
- 38. Скачать презентанцию
Лекция № 9Закон распределения Больцмана.1. Система частиц во внешнем силовом поле.2. Закон распределения Больцмана для равновесного состояния системы. 3. Барометрическая формула.
Слайды и текст этой презентации
Слайд 2 Лекция № 9
Закон распределения Больцмана.
1. Система частиц во внешнем
силовом поле.
Барометрическая формула.
Слайд 3 В отсутствие внешних сил средняя концентрация n молекул
газа в сос-тоянии равновесия всюду одинакова. Но этого не будет
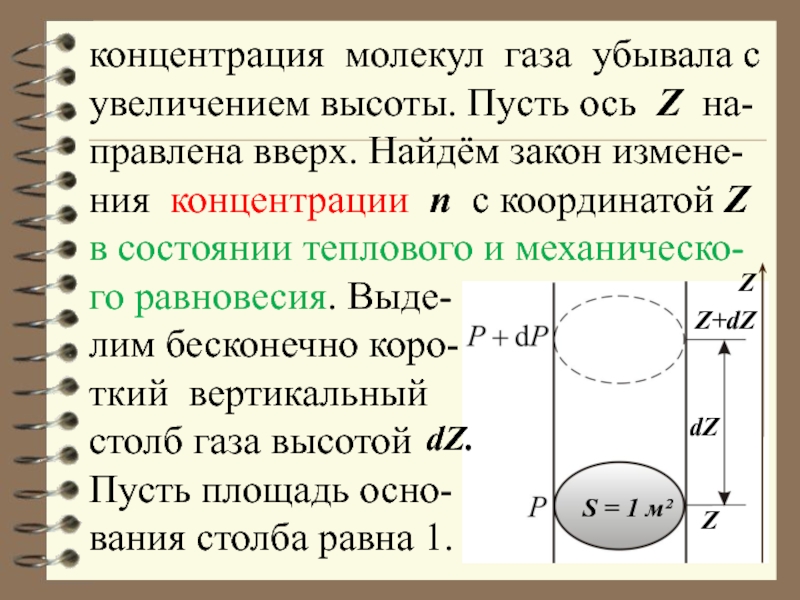
при наличии сило-вых полей. Рассмотрим, например, идеальный газ в однородном поле тяжести. В состоянии равновесия температура Т должна быть одинакова по всей толще газа (иначе возникли бы потоки тепла). Для механического равновесия необходимо, чтобы
Слайд 4концентрация молекул газа убывала с увеличением высоты. Пусть ось Z
на-правлена вверх. Найдём закон измене-ния концентрации n с координатой Z
в состоянии теплового и механическо-го равновесия. Выде-лим бесконечно коро-
ткий вертикальный
столб газа высотой
Пусть площадь осно-
вания столба равна 1.
Z
dZ
Z+dZ
Z
dZ.
S = 1 м²
Слайд 6 Вес столба n mg dZ S должен уравно-вешиваться разностью
давлений:
, т.к. S = 1 м²Z
dZ
Z+dZ
Z
S = 1 м²
Слайд 7 Физическая природа силового поля не имеет значения. Важно, чтобы
поле было постоянно и консервативно (потенциально). Если Ep – потенци-альная
энергия молекулы в силовом поле, то mg∙dZ = dEp, а потому получаем:
Слайд 8 закон
распределения
Больцмана
Закон распределения частиц по потенци-альным энергиям –
распределение Больцмана. Здесь n0 – число
молекул в единице объёма там, где .
Слайд 10
Больцман Людвиг (1844 –
1906) – австрийский физик- теоретик, один из основопо- ложников классической статистической физики. Основные работы в области кинетической теории газов, термодина-мики и теории излучения. Вывел основ-ное кинетическое уравнение газов, явля-ющееся основой физической кинетики.
Слайд 11 Пусть идеальный газ находится в поле консервативных сил, в условиях
теплового равновесия. При этом, концентрация газа будет различной в точках
с различной потенциальной энергией, что необходимо для соблюде-ния условий механического равновесия. Число молекул в единичном объеме n убывает с удалением от поверхности Земли, и давление, в силу соотношения тоже убывает.http://ido.tsu.ru/schools/physmat/data/res/models/text/molek2.htm
Слайд 13 С уменьшением температуры число молекул на высотах, отличных от нуля,
убывает. При
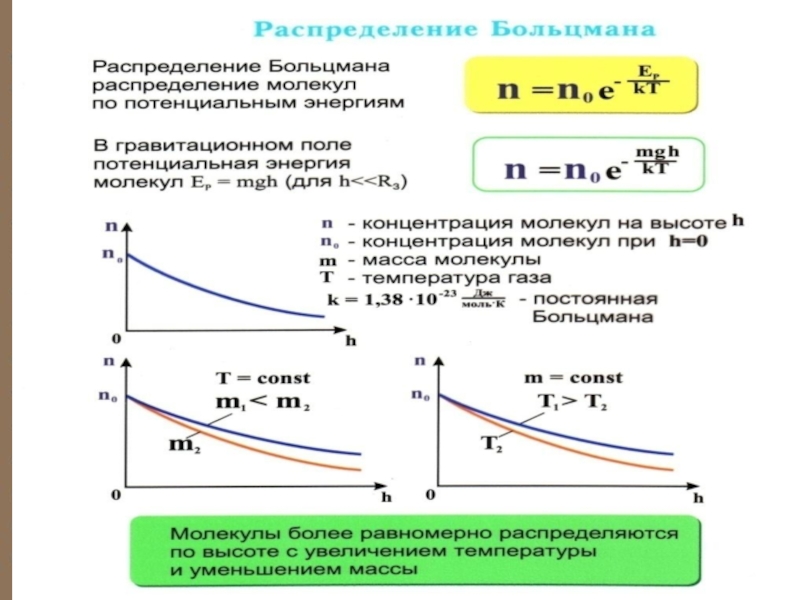
тепловое движение прекращается, все молекулы расположились бы на земной поверхности. При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой.
Слайд 14 Распределение Больцмана можно предста-вить в виде ( Ер =
mgh ):
Зависимость концентрации различных газов от высоты. Видно, что число более тяжелых молекул с высотой убывает быстрее, чем легких.
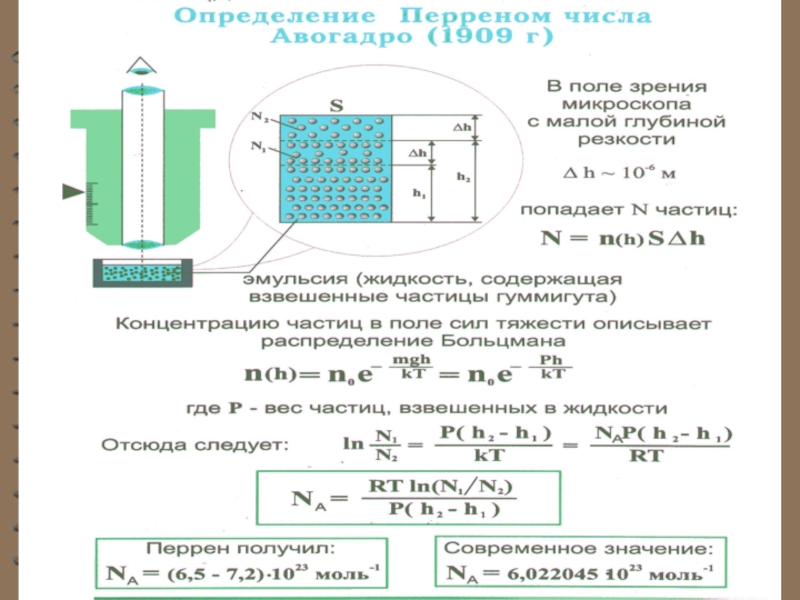
Слайд 15Опытное определение постоянной Авогадро. Ж. Перрен воспользовался идеей распределения молекул
по высоте и экспериментально определил значение постоянной Авогадро. Исследуя броуновское
движение, он убедился, что броуновские частицы распределяются по высоте подобно молекулам газа в поле тяготения. Применив к ним больцмановское распределение, можно записатьгде - масса частицы,
масса вытесненной
ею жидкости;
- радиус частицы,
- плотность частицы,
- плотность жидкости.
Слайд 16Если и - концентрации частиц
на уровнях и , а
, тоЗначение , полученное из работ Ж. Перрена, соответствовало значениям, полученным в других опытах, что подтверждает применимость к броуновским частицам распределения Больцмана.
Слайд 21 Закон распределения Максвелла-Больцмана
На прошлой лекции мы получили
выражение для распределения молекул по скоростям (распределение Максвелла), т.е. число
молекул в единице объёма, скорости которых лежат в пределах от υ до равно:
Слайд 22 Закон Максвелла даёт распределение частиц по значениям кинетической энергии
Екин, а закон Больцмана – распределение частиц по
значениям потенциальной энергии Ер. Оба распреде-ления можно объединить в единый закон Максвелла-Больцмана, согласно которому, число молекул в единице объёма, скорости которых лежат в пределах от υ до равно: (2.6.3)
Слайд 23 Обозначим
– полная энергия. Тогда
Это и есть закон распределения Максвелла-Больцмана. Здесь n0 – число молекул в единице объёма в той точке, где ; .
Слайд 24 В последнем выражении, потенциальная и кинетическая энергии, а следовательно
и полная энергия Е, могут принимать непрерывный ряд значений. Если
же энергия частицы может принимать лишь дискретный ряд значений Е1, Е2 ... (как это имеет место, например, для внутрен-ней энергии атома), то в этом случае распределение Больцмана имеет вид: ,
Слайд 25где Ni – число частиц, находящихся в состоянии с энергией
Еi, а А – коэффициент пропорциональности, который должен
удовлетворять условию: где N – полное число частиц в рассматриваемой системе.
Слайд 26 Тогда, окончательное выражение распределения Масвелла-Больцмана для случая дискретных значений будет
иметь вид:
Слайд 27 Барометрическая формула
Атмосферное давление на какой-либо
высоте h обусловлено весом выше лежащих слоёв газа.
Пусть P – давление на высоте h, а – на высоте .Выведем закон изменения давления с высо-той, предполагая, что 1) поле тяготения однородно, 2) температура постоянна и
3) масса всех молекул одинакова.
Слайд 29 Причём ,
dР < 0, так как на большей высоте давление меньше.
Раз-ность давления равна весу газа, заключённого в объёме цилиндра с площадью основания равного единице и высотой dh, ρ плотность газа на высоте h, медленно убывает с высотой. Отсюда где P0 – давление на высоте - барометрическая
формула
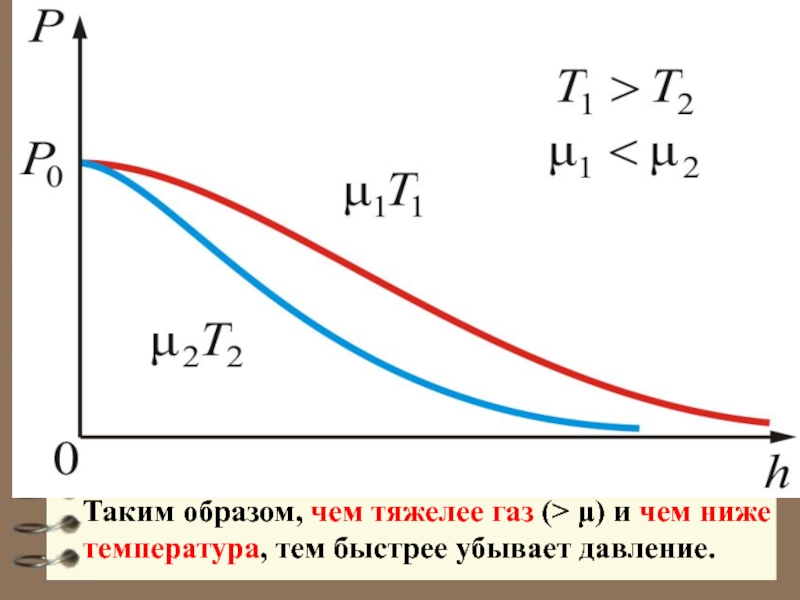
Слайд 30 Из барометрической формулы следует, что P убывает с
высотой тем быстрее, чем тяжелее газ (чем больше μ) и
чем ниже температура (например, на больших высотах концентрация легких газов Не и Н2 гораздо больше чем у поверхности Земли). На рисунке изображены две кривые, которые можно трактовать, либо как соответствующие разным μ (при одинаковой Т), либо как отвечающие разным Т, при одинаковых μ.
Слайд 33 Распределение Бозе-Эйнштейна
и Ферми-Дирака
Если
у нас имеется термодинами-ческая система состоящая из N частиц, энергии
которых могут принимать дискретные значения , то говорят о системе квантовых чисел.Поведение такой системы описыва-ется квантовой статистикой, в осно-ве которой лежит принцип неразличи-мости тождественных частиц.
Слайд 34 Основная задача квантовой статистики состоит в определении среднего числа
частиц
, находящихся в ячейке фазового пространства: «координаты – проекции импульса» (x, y, z и px, py, pz) частиц. При этом имеют место два закона распределения частиц по энергиям (две статистики):
Слайд 36 Первая формула описывает квантовые частицы с целым спином (собственный момент
количетсва движения). Их называют бозоны (например, фотоны). Вторая формула описывает
квантовые частицы с полуцелым спином. Их называют фермионы (например: электроны, протоны, нейтрино).
