Слайд 1Транспортные задачи
Двухиндексные задачи линейного программирования
Слайд 2Классическая постановка задачи
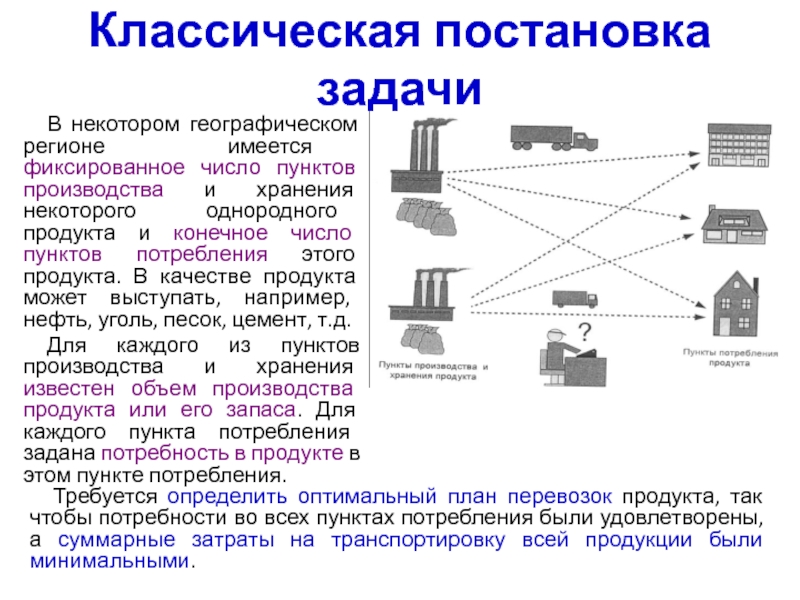
В некотором географическом регионе имеется фиксированное число пунктов
производства и хранения некоторого однородного продукта и конечное число пунктов
потребления этого продукта. В качестве продукта может выступать, например, нефть, уголь, песок, цемент, т.д.
Для каждого из пунктов производства и хранения известен объем производства продукта или его запаса. Для каждого пункта потребления задана потребность в продукте в этом пункте потребления.
Требуется определить оптимальный план перевозок продукта, так чтобы потребности во всех пунктах потребления были удовлетворены, а суммарные затраты на транспортировку всей продукции были минимальными.
Слайд 3Математическая постановка
сij – стоимость перевозки от i-го поставщика к j-ому
потребителю;
хij – объём перевозки от i-го поставщика к j-ому потребителю;
Слайд 4Математическая модель задачи
План
, при котором функция F(X) принимает своё минимальное значение, называется оптимальным планом транспортной задачи.
Слайд 5Выбор критерия оптимальности
Оценка экономической эффективности примерного плана может определятся по тому или
иному критерию, положенному в основу расчета плана. Этот критерий является экономическим
показателем, характеризующим качество плана.
До настоящего времени нет общепринятого единого критерия всесторонне учиты-вающего экономические факторы. При решении транспортной задачи, в качестве критерия оптимальности в различных случаях используют следующие показатели:
Слайд 6Показатели оптимальности
1) Объем работы транспорта
(критерий - расстояние
в т/км).
Минимум пробега удобен для оценки планов перевозок, поскольку
расстояние перевозки определяется легко и точно для любого направления. Поэтому критерию нельзя решать транспортные задачи с участием многих видов транспорта.
С успехом применяется при решении транспортных задач для автомобильного транспорта и при разработке оптимальных схем перевозки однородных грузов автомобилями.
Слайд 7Показатели оптимальности
2) Тарифная плата за перевозку груза (критерий - тарифы
провозных плат).
Позволяет получить схему перевозок, наилучшую с точки зрения
хозрасчетных показателей предприятия.
Все надбавки, а также существующие льготные тарифы затрудняют его использование.
Слайд 8Показатели оптимальности
3) Эксплуатационные расходы на транспортировку грузов
(критерий - себестоимость
эксплуатационных расходов).
Более верно отражает экономичность перевозок различными видами транспорта.
Позволяет делать обоснованные выводы о целесообразности переключения с одного вида транспорта на другой.
Слайд 9Показатели оптимальности
4) Сроки доставки грузов
(критерий - затраты времени).
T –
время доставки;
lуч – расстояние;
vуч – скорость доставки;
Tтех – время техобслуживания.
Слайд 10Показатели оптимальности
5) Приведенные затраты (с учетом эксплуатационных расходов, зависящих от
размеров движения и капиталовложения в подвижной состав).
Слайд 11Показатели оптимальности
6) Приведенные затраты (с учетом полных эксплуатационных расходов капиталовложений
на строительство объектов в подвижной состав).
где Сприв - эксплуатационные издержки;
Сзав – заводские издержки;
Кэф - расчетный коэффициент эффективности капиталовложения;
Кп- капитальные вложения, приходящие на 1 т груза на протяжении участка;
Т - время следования;
Ц - цена одной тоны груза.
Позволяет более полно производить оценку рационализации разных вариантов планов перевозок, с достаточно полным учётом одновременного влияния нескольких экономических факторов
Слайд 12Условие разрешимости транспортной задачи
Теорема: Для разрешимости транспортной задачи необходимо и
достаточно, чтобы запасы груза в пунктах отправления были равны потребности
в грузе в пунктах назначения, т. е. чтобы выполнялось равенство:
Модель такой транспортной задачи называется сбалансированной или закрытой, или замкнутой.
В противном случае модель называется открытой.
Слайд 13Условие разрешимости транспортной задачи
В случае
вводится
фиктивный (n+1)-й пункт назначения с потребностью , и соответствующие тарифы считаются равными нулю: ci, n+1 = 0, i=1,m .
Аналогично, при вводится фиктивный (m+1)-й пункт отправления с запасом груза , и соответствующие тарифы считаются равными нулю: cm+1 , j =0, j=1,n.
Этим задача сводится к закрытой транспортной задаче.
Слайд 14Условие разрешимости транспортной задачи
Число переменных xij в транспортной задаче с
m пунктами отправления и n пунктами назначения равно m·n, а
число уравнений в системе – n + m.
Тогда число линейно независимых уравнений равно
n + m – 1.
Поэтому опорный план может иметь не более
n + m – 1 отличных от нуля неизвестных.
Если в опорном плане число отличных от нуля компонент равно в точности n + m – 1, то план называется невырожденным, а если меньше – то вырожденным.
Слайд 15Общий алгоритм аналитического решения транспортной задачи
методом потенциалов
Находим первоначальный допустимый
план (методы северо-западного угла, минимального элемента, двойного предпочтения, метод Фогеля);
проверяем
полученный план на оптимальность (применяя свойства двойственных ЗЛП);
пока план не оптимальный переходим к плану с меньшей стоимостью перевозок.
Слайд 16Нахождение первоначального допустимого плана
1. Метод северо-западного угла.
При нахождении опорного
плана на каждом шаге рассматривают первый из оставшихся пунктов отправления
и первый из оставшихся пунктов назначения. Заполнение клеток таблицы условий начинается с левой верхней клетки для неизвестного x11 («северо-западный угол») и заканчивается клеткой для неизвестного xmn, т.е. как бы по диагонали таблицы.
Слайд 17Нахождение первоначального допустимого плана
2. Метод наименьшей стоимости.
Из всей таблицы
стоимостей выбирают наименьшую и в клетку (i, j), которая ей
соответствует, помещают меньшее из чисел ai и bj .
Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя.
Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс размещения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.
Слайд 18Нахождение первоначального допустимого плана
3. Метод двойного предпочтения.
В каждом столбце
отмечают знаком «√» клетку с наименьшей стоимостью. Затем то же
проделывают в каждой строке. В результате некоторые клетки имеют отметку «√√». В них находится минимальная стоимость, как по столбцу, так и по строке.
В эти клетки помещают максимально возможные объемы перевозок, каждый раз исключая из рассмотрения соответствующие столбцы или строки.
Затем распределяют перевозки по клеткам, отмеченным знаком «√». В оставшейся части таблицы перевозки распределяют по наименьшей стоимости.
Слайд 19Нахождение первоначального допустимого плана
4. Метод аппроксимации Фогеля.
При определении опорного
плана данным методом на каждой итерации по всем столбцам и
всем строкам находят разность между двумя записанными в них минимальными тарифами.
Эти разности заносят в специально отведенные для этого строки и столбцы в таблице условий задачи.
Среди указанных разностей выбирают максимальную. В строке (или столбце), который данная разность соответствует, определяют минимальный тариф. Клетку, в которой он записан, заполняют на данной итерации.
Слайд 20Построенный первоначальный план транспортной задачи как задачи линейного программирования можно
было бы довести до оптимального с помощью симплексного метода.
Однако
из-за громоздкости симплексных таблиц, содержащих тn неизвестных, и большого объема вычислительных работ для получения оптимального плана используют более простые методы.
Слайд 21Метод потенциалов – нахождение оптимального плана
Составим двойственную задачу
u1, u2,…,um,
v1, v2,…, vn – двойственные переменные;
целевая функция: ;
ограничения:
Слайд 22Метод потенциалов
Теорема (критерий оптимальности)
Для того чтобы допустимый план перевозок в транспортной
задаче
был оптимальным, необходимо и достаточно, чтобы существовали такие числа u1, u2,…,um,v1, v2,…, vn , что
ui + vj =cij, если xij > 0,
ui + vj < cij, если xij ≤ 0.
Числа ui и vj называются потенциалами пунктов отправления Ai и назначения Bj соответственно.
Слайд 23Алгоритм нахождения оптимального решения транспортной задачи методом потенциалов
1. Пусть одним
из рассмотренных выше методов найден опорный план.
2. Для базисных
клеток плана (их m + n – 1), определяем потенциалы ui и vj так, чтобы выполнялось условие
ui. + vj = cij .
Поскольку система ограничений содержит m + n – 1 уравнений и m + n неизвестных, то одну из них можно задать произвольно (например, приравнять к нулю). После этого определяются остальные потенциалы.
3. Для каждой из свободных клеток вычисляются величины
wij. = ui. + vj – cij.
4. Если оказалось, что wij < 0, то план оптимален. Если же хотя бы в одной свободной клетке wij > 0, то план не является оптимальным и может быть улучшен путем переноса по циклу, соответствующему данной свободной клетке.
Слайд 24Алгоритм нахождения оптимального решения транспортной задачи методом потенциалов
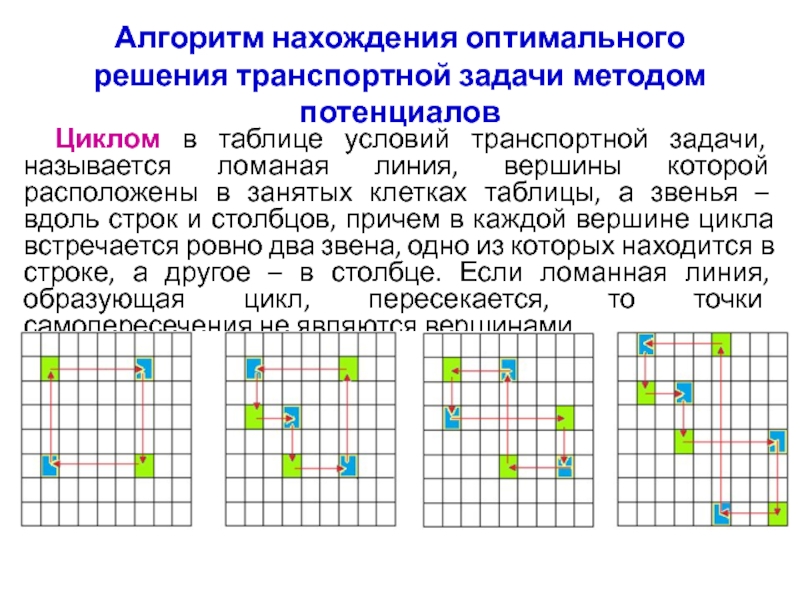
Циклом в таблице
условий транспортной задачи, называется ломаная линия, вершины которой расположены в
занятых клетках таблицы, а звенья – вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно два звена, одно из которых находится в строке, а другое – в столбце. Если ломанная линия, образующая цикл, пересекается, то точки самопересечения не являются вершинами.
Слайд 25Пример
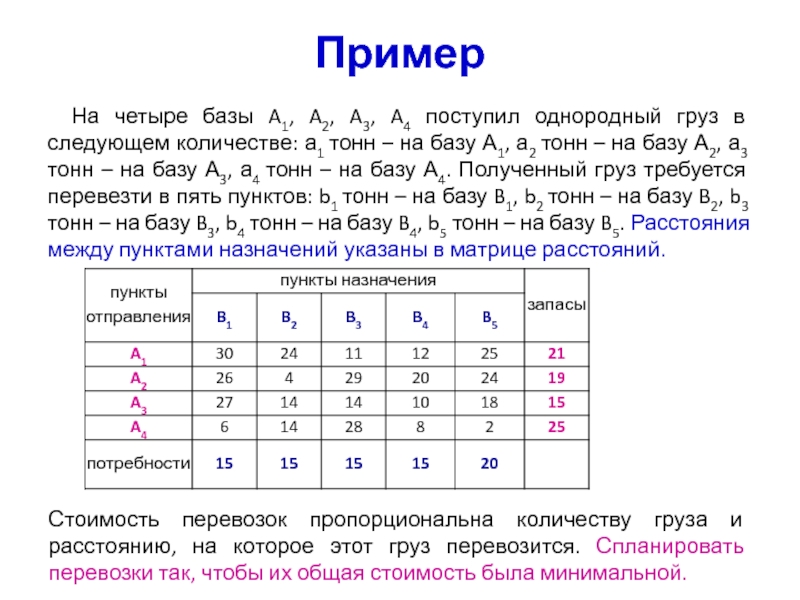
На четыре базы A1, A2, A3, A4 поступил однородный груз
в следующем количестве: а1 тонн – на базу А1, а2
тонн – на базу А2, а3 тонн – на базу А3, а4 тонн – на базу А4. Полученный груз требуется перевезти в пять пунктов: b1 тонн – на базу B1, b2 тонн – на базу B2, b3 тонн – на базу B3, b4 тонн – на базу B4, b5 тонн – на базу B5. Расстояния между пунктами назначений указаны в матрице расстояний.
Стоимость перевозок пропорциональна количеству груза и расстоянию, на которое этот груз перевозится. Спланировать перевозки так, чтобы их общая стоимость была минимальной.



























![Автоматизация звука [ л ].
Артикуляционная гимнастика
Звук [ л ]
Звук [ л ] в](/img/thumbs/d768b5f485a8ee137695f1baa4360e4f-800x.jpg)













