Тригонометрические

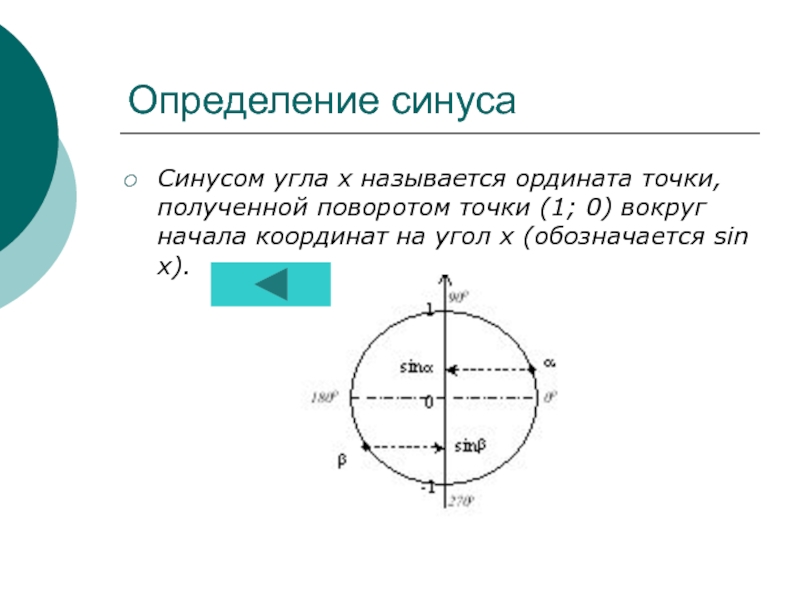
график синуса..........................10 слайд
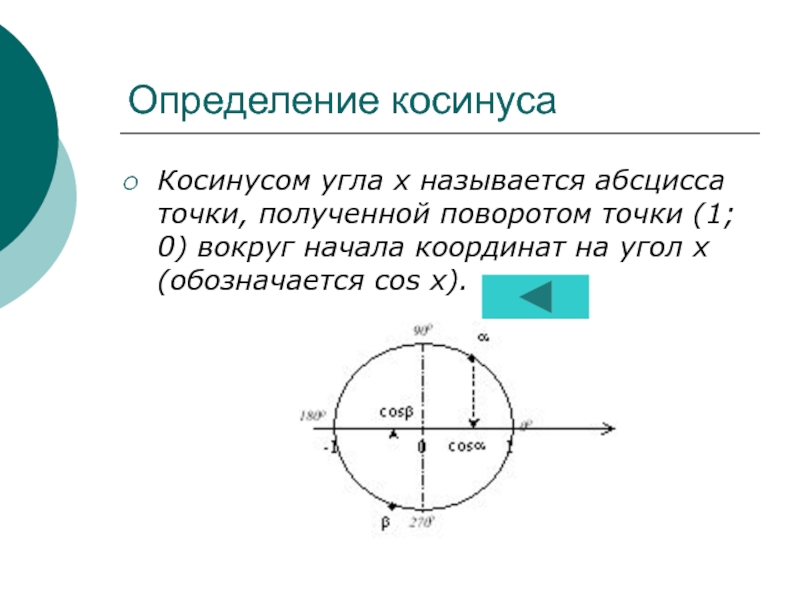
Определение и график косинуса......................11 слайд
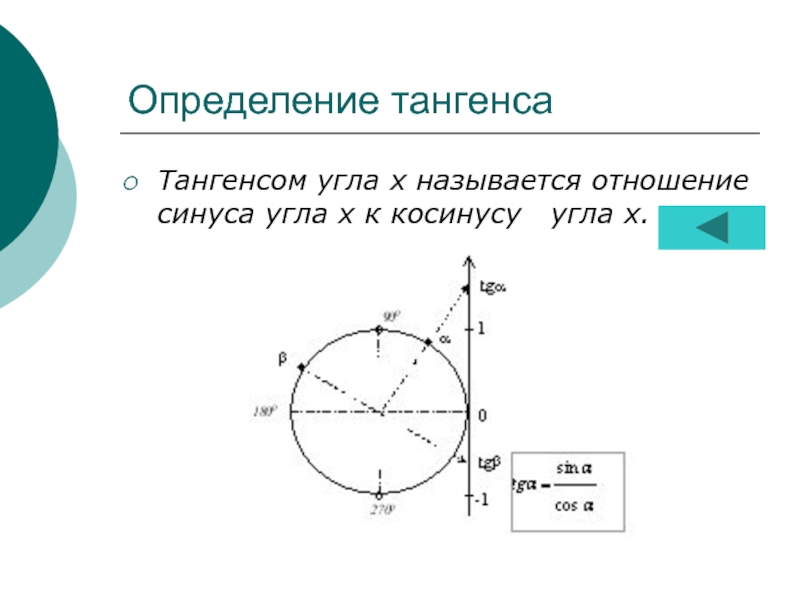
Определение и график тангенса.......................12

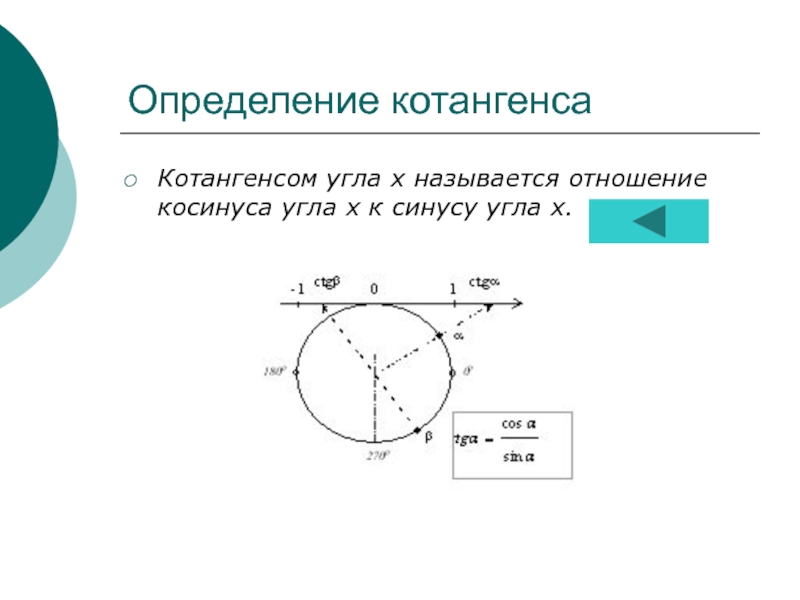
слайд
Определение и график котангенса...................13 слайд
Обратные тр-ие функции.........................................14 слайд
Основные формулы.............................................15-16 слайд
Значение тригонометрии..........................................17 слайд
Используемая литература........................................18 слайд
Автор и составитель..................................................19 слайд

и строительного дела, то есть носила чисто геометрический характер и

представляла главным образом «исчисление хорд». Со временем в нее начали вкрапляться некоторые аналитические моменты. В первой половине 18-го века произошел резкий перелом, после чего тригонометрия приняла новое направление и сместилась в сторону математического анализа. Именно в это время тригонометрические зависимости стали рассматриваться как функции. Это имеет не только математико-исторический, но и методико-педагогический интерес.

аргумента уделяется большое внимание в школьном курсе алгебры и начал

анализа. Существует несколько различных подходов к преподаванию данной темы в школьном курсе, и учитель, особенно начинающий, легко может запутаться в том, какой подход является наиболее подходящим. А ведь тригонометрические функции представляют собой наиболее удобное и наглядное средство для изучения всех свойств функций (до применения производной), а в особенности такого свойства многих природных процессов как периодичность. Поэтому их изучению следует уделить пристальное внимание.

школьном курсе возникают из-за несоответствия между достаточно большим объемом содержания

и относительно небольшим количеством часов, выделенным на изучение данной темы. Таким образом, проблема этой исследовательской работы состоит в необходимости устранения этого несоответствия за счет тщательного отбора содержания и разработки эффективных методов изложения данного материала. Объектом исследования является процесс изучения функциональной линии в курсе старшей школы. Предмет исследования - методика изучения тригонометрических функций в курсе алгебры и начала анализа в 10-11 классе.

«Тригонометрические функции»
в курсе алгебры и математического анализа.

изучении геометрии, а также при исследовании периодических процессов. Обычно тригонометрические

функции определяют как отношения сторон прямоугольного треугольника или длины определённых отрезков в единичной окружности. Более современные определения выражают тригонометрические функции через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на произвольные вещественные числа и даже на комплексные числа.

с тригонометрическими функциями углового аргумента в геометрии. Значение аргумента рассматривается

в промежутке (0о;90о). На этом этапе учащиеся узнают, что sin, сos, tg и ctg угла зависят от его градусной меры, знакомятся с табличными значениями, основным тригонометрическим тождеством и некоторыми формулами приведения.
II. Обобщение понятий синуса, косинуса, тангенса и котангенса для углов (0о;180о). На этом этапе рассматривается взаимосвязь тригонометрических функций и координат точки на плоскости, доказываются теоремы синусов и косинусов, рассматривается вопрос решения треугольников с помощью тригонометрических соотношений.
III. Введение понятий тригонометрических функций числового аргумента.
IV. Систематизация и расширение знаний о тригонометрических функциях числа, рассмотрение графиков функций, проведение исследования, в том числе и с помощью производной.

две группы: аналитические и геометрические.
К аналитическим способам относят определение

функции у = sin х как решения дифференциального уравнения
f (х)=-c*f(х)
или как сумму степенного ряда
sin х = х - х3 /3!+ х5 /5! - …
2. К геометрическим способам относят определение тригонометрических функций на основе проекций и координат радиус-вектора, определение через соотношения сторон прямоугольного треугольника и определения с помощью числовой окружности. В школьном курсе предпочтение отдается геометрическим способам в силу их простоты и наглядности.

(1; 0) вокруг начала координат на угол х (обозначается sin

x).

(1; 0) вокруг начала координат на угол х (обозначается cos

x).

косинусу угла х.

синусу угла х.

и ctg х
можно определить обратные функции. Они обозначаются соответственно

arcsin х (читается «арксинус x»), arcos x, arctg x и arcctg x.

тригонометрических задач.

БЕСКОНЕЧНО!
Это одна из составляющих наук на многих факультетах институтов

нашей страны!!!
Это одна из тех наук, в которую были вложены труды таких ученых, как Евклид, Архимед, Аполлоний, Птолемей, Ф.Виет, И.Бернулли, Н.И.Лобачевский, Д.Е.Меньшов, Н.К.Бари и многих, многих других!!!

И в конце своей презентации я хотела бы сказать, что:

начала анализа».
Г.Бирюков, А.А.Бряндинская «Энциклопедия юного математика»

класса,г.Обнинска!