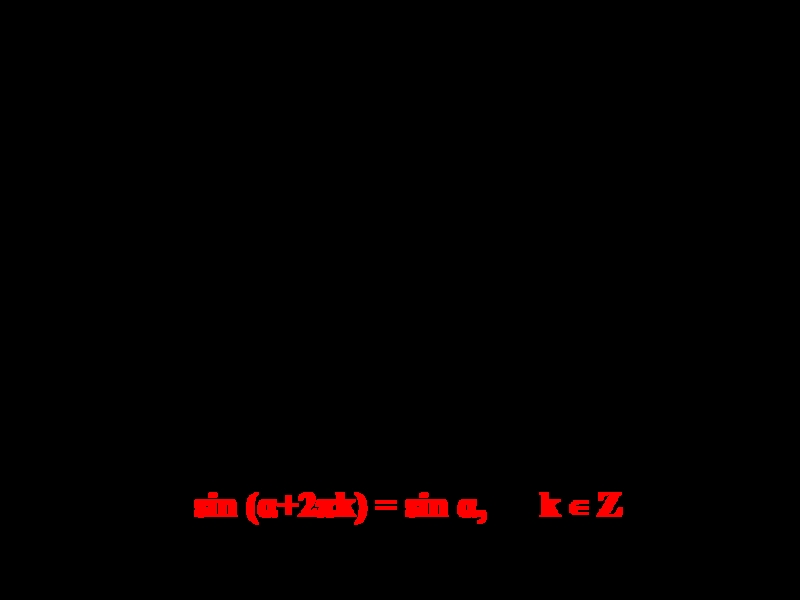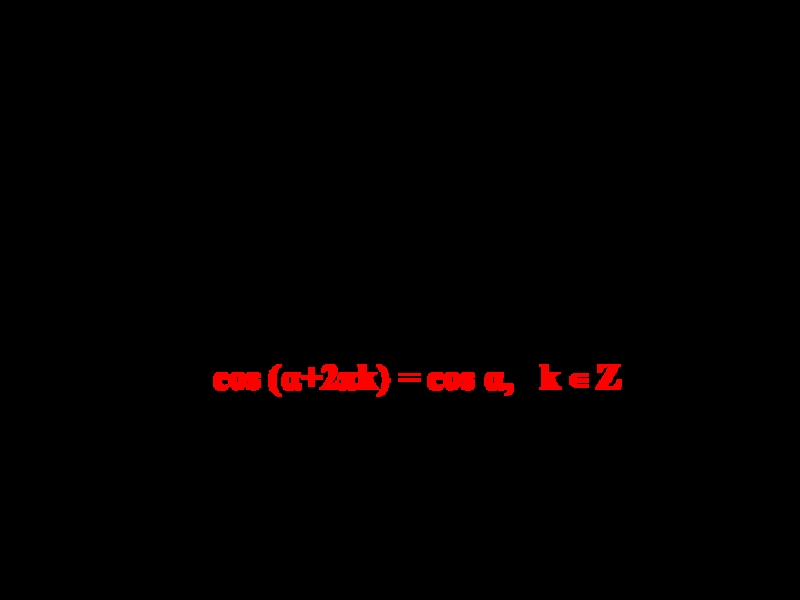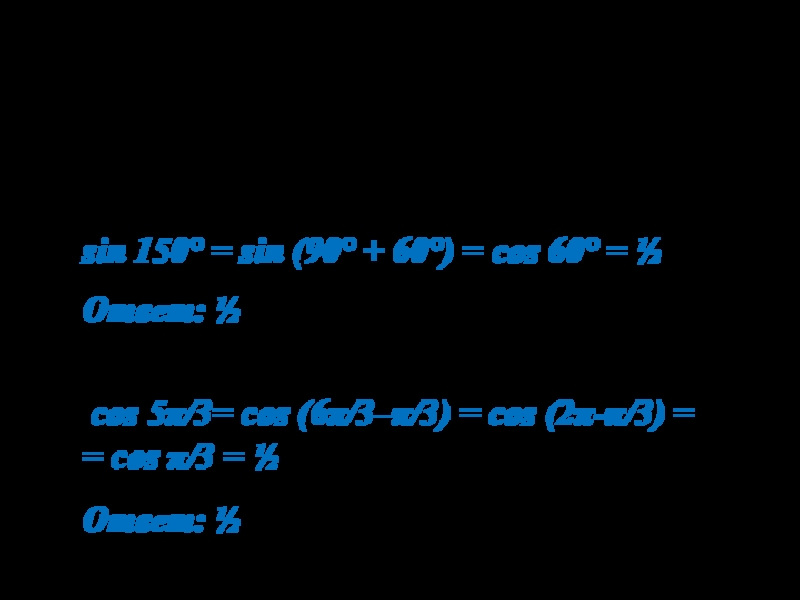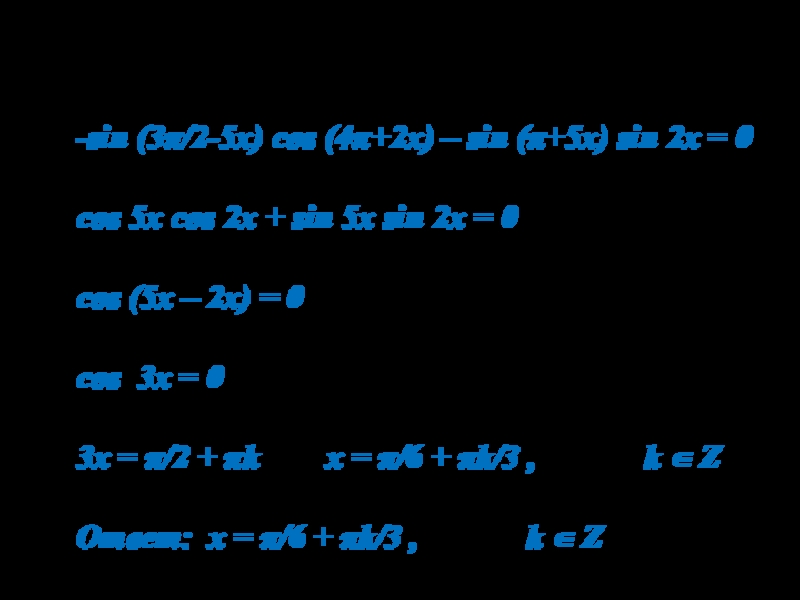Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тригонометрия
Содержание
- 1. Тригонометрия
- 2. Формулы приведения Таблицы значений синуса, косинуса,
- 3. Вычислить sin 750°Очевидно, что 750° = 2
- 4. Следовательно, верна формула cos (α+2πk)
- 5. Слайд 5
- 6. Используя формулы сложения для синуса и косинуса,
- 7. cos (π/2 – α) = sin
- 8. Упражнения:Найти значение sin α для острого угла: sin
- 9. 3. Решить уравнения:1). cos (π/2 – x)
- 10. 3). sin (5x-3π/2) cos (2x+4π) – sin
- 11. Составьте таблицу формул приведения
- 12. ЖЕЛАЮ УСПЕХОВ
- 13. Скачать презентанцию
Формулы приведения Таблицы значений синуса, косинуса, тангенса и котангенса составляются для углов от 0° до 90°. Это объясняется тем, что их значения для остальных углов сводятся к значениям для острых
Слайды и текст этой презентации
Слайд 3Вычислить sin 750°
Очевидно, что 750° = 2 · 360° +
30°.
Поэтому sin 750°= sin 30°= ½.
Следовательно, верна формула:
sin (α+2πk) = sin α, k ZСледовательно, при повороте единичного радиуса вокруг начала координат на 750° точка Р (1; 0) совершит два полных оборота и ещё повернётся на угол 30°, т.е. получится тот же самый угол, что и при повороте на 30°.
Слайд 4 Следовательно, верна формула
cos (α+2πk) = cos α,
k Z
Точно так же вычисляется cos 780°.
cos 780°=cos
(2 · 360°+60°) = cos 60° = ½ 
Слайд 6Используя формулы сложения для синуса и косинуса, мы получаем формулы
приведения:
sin (π/2 – α) = cos α
sin
(π/2 + α) = cos α sin (π – α) = sin α
sin (π + α) = - sin α
sin (3π/2–α)= - cos α
sin (3π/2+α) = - cos α
Слайд 7 cos (π/2 – α) = sin α
cos
(π/2 + α)= - sin α
cos (π – α)
= - cos αcos (π + α) = - cos α
cos (3π/2 – α)= - sin α
cos (3π/2 + α) = sin α
Слайд 8Упражнения:
Найти значение sin α для острого угла:
sin 150°;
sin 150° =
sin (90° + 60°) = cos 60° = ½
Ответ: ½
2.
Вычислить: cos 5π/3; cos 5π/3= cos (6π/3–π/3) = cos (2π-π/3) = = cos π/3 = ½
Ответ: ½
Слайд 93. Решить уравнения:
1). cos (π/2 – x) = 1
sin x
= 1
x = π/2 + 2πk k
ZОтвет: x = π/2 + 2πk , k Z
2). sin (3π/2 + x) =1
cos x = 1
cos x = - 1
x = π + 2πk , k Z
Ответ: x = π + 2πk , k Z
Слайд 103). sin (5x-3π/2) cos (2x+4π) – sin (5x+π) sin 2x
= 0
-sin (3π/2-5x) cos (4π+2x) – sin (π+5x) sin 2x
= 0cos 5x cos 2x + sin 5x sin 2x = 0
cos (5x – 2x) = 0
cos 3x = 0
3x = π/2 + πk x = π/6 + πk/3 , k Z
Ответ: x = π/6 + πk/3 , k Z
