Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Учитель математики Потапова Е.А. Степенная функция её свойства и
Содержание
- 1. Учитель математики Потапова Е.А. Степенная функция её свойства и
- 2. Вы знакомы с функциями у=х, у=х2, у=хЗ,
- 3. Виды степенной функции
- 4. Рис. 1
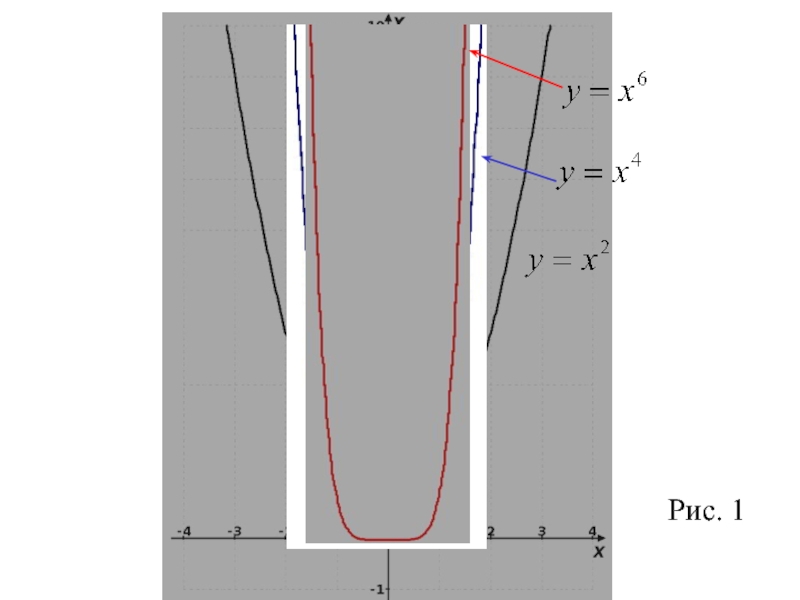
- 5. Показатель р=2n - четное натуральное число. В
- 6. Рис.2
- 7. 2. Показатель р=2n -1 - нечетное
- 8. Рис.3
- 9. 3. Показатель р = - 2n, где
- 10. Рис.4
- 11. 4. Показатель р = - (2n -
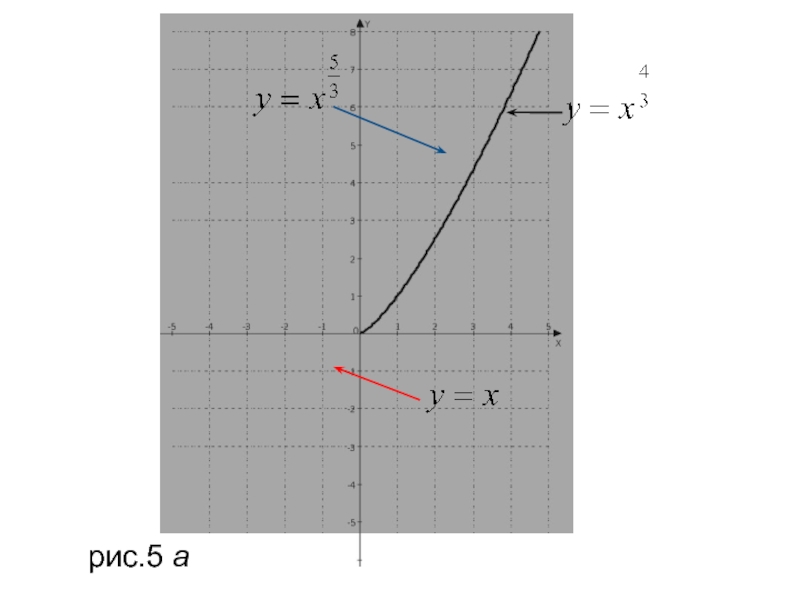
- 12. рис.5 a
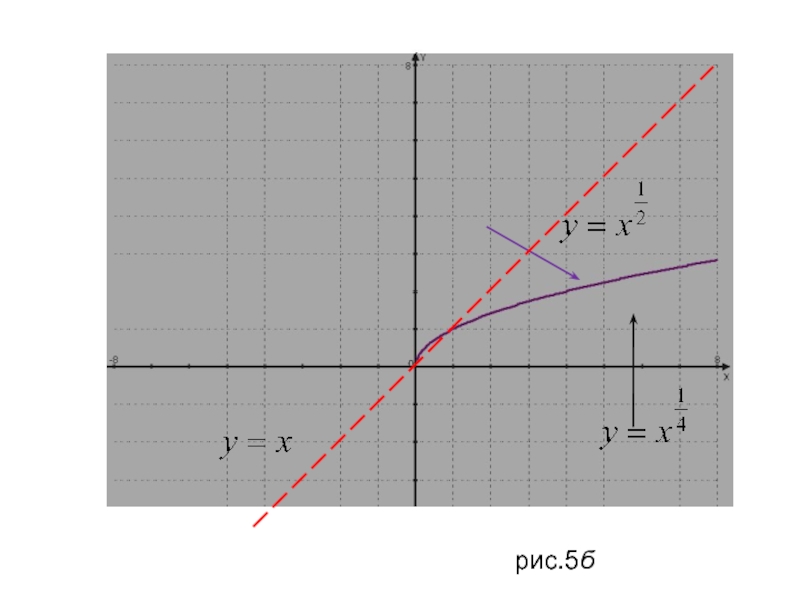
- 13. рис.5б
- 14. Показатель р - положительное действительное нецелое
- 15. Показатель р - положительное действительное нецелое
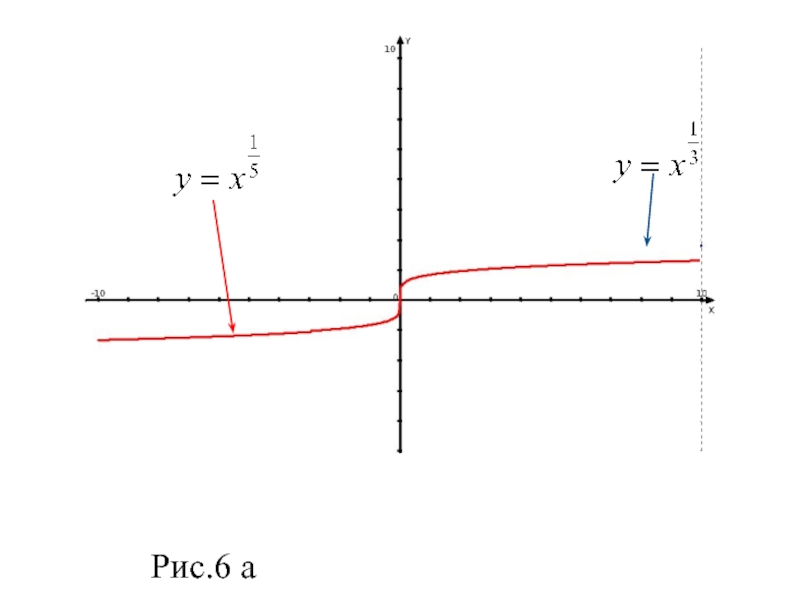
- 16. Рис.6 а
- 17. Показатель -р - отрицательное действительное нецелое
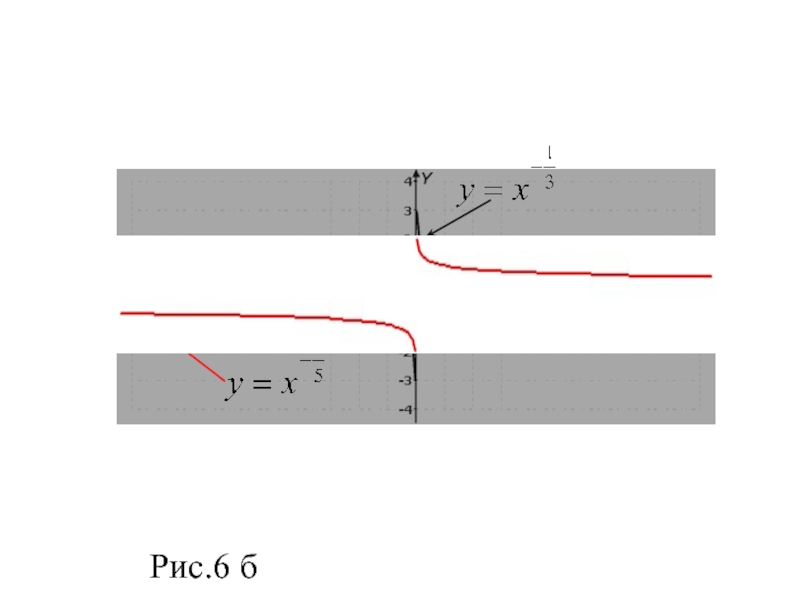
- 18. Рис.6 б
- 19. Показатель -р - отрицательное действительное нецелое
- 20. Рис.6 в
- 21. Скачать презентанцию
Вы знакомы с функциями у=х, у=х2, у=хЗ, у=1/х и т. д. Все эти функции являются частными случаями степенной функции, т. е. функции у = хР, где р - заданное действительное число.
Слайды и текст этой презентации
Слайд 2Вы знакомы с функциями у=х, у=х2, у=хЗ, у=1/х и т.
д. Все эти функции являются частными случаями степенной функции,
т.
е. функции у = хР, где р - заданное действительное число. Свойства и график степенной функции существенно зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях х и р имеет смысл степень хР. Перейдем к подробному рассмотрению различных случаев в зависимости от показателя степени р. Слайд 5Показатель р=2n - четное натуральное число. В этом случае степенная
функция
у = х2n, где n - натуральное число, обладает
следующими свойствами: Область определения - все действительные числа,
т. е. множество R ;
множество значений - неотрицательные числа, т. е. y≥ 0;
функция у=х2n четная, так как (-х)2n = х2n;
функция является убывающей на промежутке x≤O и возрастающей на промежутке x ≥O.
График функции у = хР имеет такой же вид, как, например, график функции у = х4 (рис. 1).
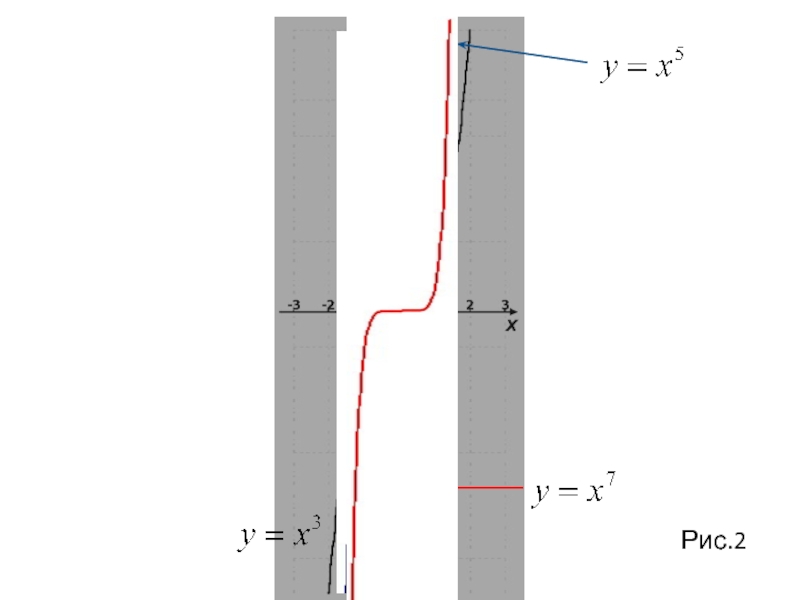
Слайд 72. Показатель р=2n -1 - нечетное
натуральное число.
В этом
случае степенная функция y = х2n-1,
где 2n-1 - натуральное
число, обладает следующими свойствами: - область определения - множество R;
- множество значений - множество R;
Функция y = х2n-1 нечетная, так как
(-х)2n-1=- х2n-1;
- функция является возрастающей на всей действительной оси.
График функции y = х2n-1 имеет такой же вид, как, например, график функции y = х3 (рис. 2).
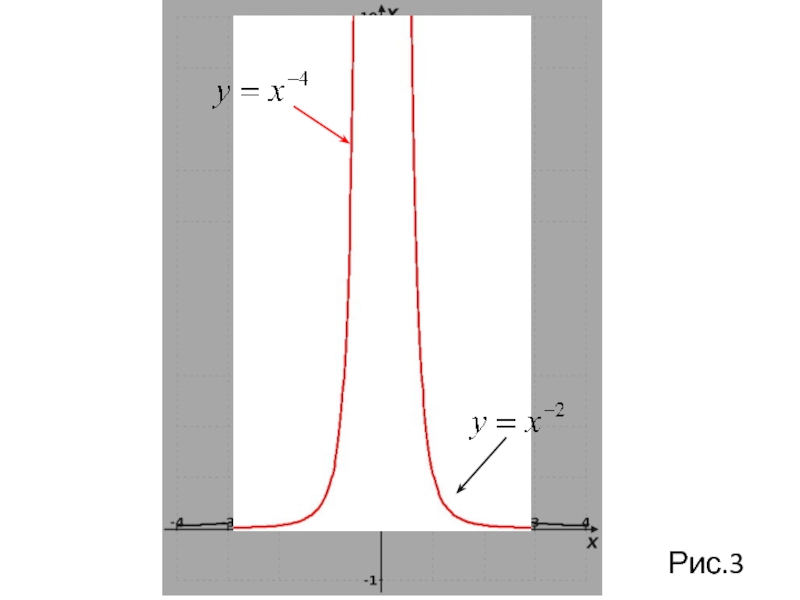
Слайд 93. Показатель р = - 2n, где n - натуральное
число.
В этом случае степенная функция y=х -2n обладает следующими
свойствами: - область определения - множество R, кроме х= 0;
- множество значений - положительные числа у>0;
- Функция y=х -2n - четная, так как (-х) -2n = х-2n;
функция является возрастающей на промежутке х<0 и убывающей на промежутке х>0.
График функции y=х-2nимеет такой же вид, как, например, график функции y=х-2 (рис.3).
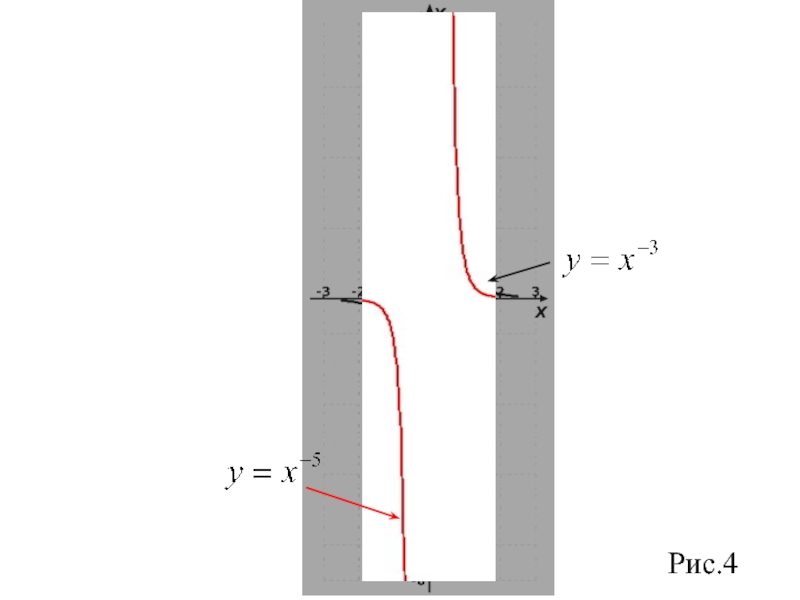
Слайд 114. Показатель р = - (2n - 1), где n
- натуральное число.
В этом случае степенная функция y=х-(2n-1) обладает
следующими свойствами: - область определения - множество R, кроме х=0;
- множество значений - множество R, кроме у=0;
- функция нечетная, так как (-х)-(2n-1) = -х-(2n-1);
- функция является убывающей на промежутках х<0 и х>0.
График функции y=х-(2n-1) имеет такой же вид, как, например, график функции y=х-3 (рис. 4).
Рис.4
Слайд 14 Показатель р - положительное действительное нецелое число,(p-несократимая обыкновенная дробь
вида 2m/2n+1 или 2m+1/2n)
В этом случае функция у=хР обладает следующими
свойствами: область определения х≥0;
множество значений у≥0;
функция является возрастающей на промежутке [0; ∞).
График функции у=хР, где р - положительное нецелое число, имеет такой же вид, как, например, график
Функции (при 0<р< 1) или как, например,
график функции (при p>1) (рис.5 a, б),если числитель или знаменатель является четным числом.
Слайд 15 Показатель р - положительное действительное нецелое число,(p-несократимая обыкновенная дробь
вида 2m+1/2n+1)
В этом случае функция у=хР обладает следующими свойствами:
область
определения хϵ R множество значений уϵ R
функция является возрастающей на промежутке R .
График функции у=хР, где р - положительное нецелое число, имеет такой же вид, как, например,
график функции (при 0<р< 1).
Слайд 17 Показатель -р - отрицательное действительное нецелое число,(p-несократимая обыкновенная дробь
вида 2m+1/2n+1)
В этом случае функция у=х-р обладает следующими свойствами:
область
определения хϵ R ,кроме х=0, множество значений уϵ R, кроме х=0.
функция убывает на каждом промежутке области определения.
График функции у=х-р, где -р – отрицательное нецелое число, имеет такой же вид, как, например,
график функции (при 0<р< 1) на рисунке 6 б.
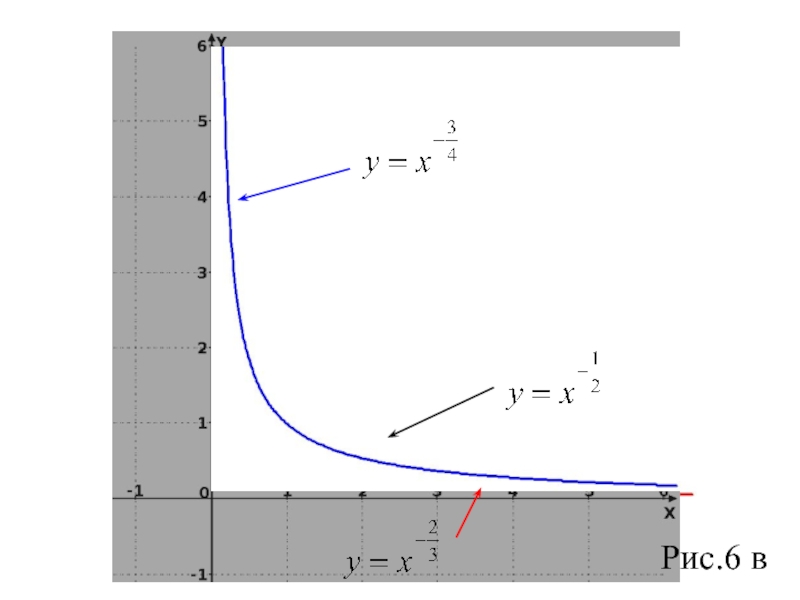
Слайд 19 Показатель -р - отрицательное действительное нецелое число,(p-несократимая обыкновенная дробь
вида или 2m/2n+1)
В этом случае функция у=х-р обладает следующими свойствами:
область определения х>0,
множество значений у>0.
функция убывает на промежутке(0; ∞).
График функции у=х-р, где -р – отрицательное нецелое число вида 2m+1/2n или 2m/2n+1 , имеет такой же вид, как, например,график функции
(при -1<-р< 0) на рисунке 6 б.