Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Угол между векторами. Скалярное произведение векторов
Содержание
- 1. Угол между векторами. Скалярное произведение векторов
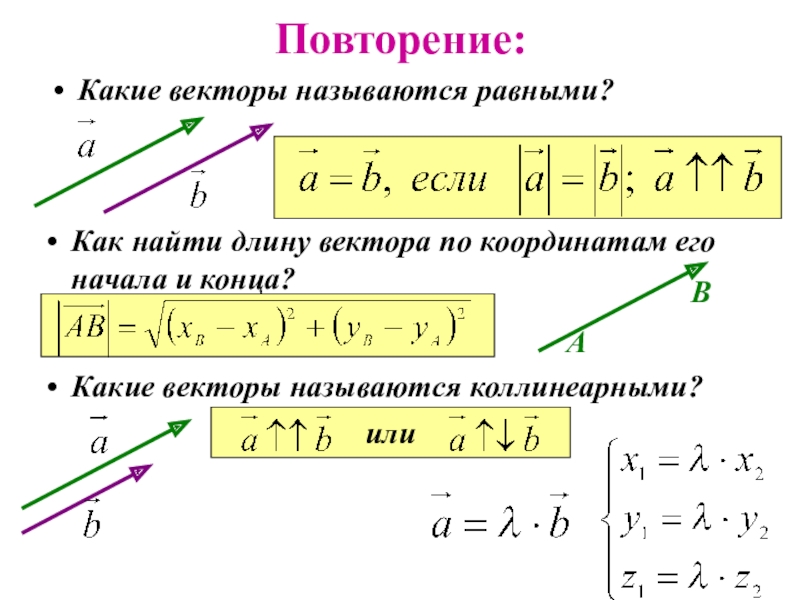
- 2. Повторение:Какие векторы называются равными?Как найти длину вектора по координатам его начала и конца?АВКакие векторы называются коллинеарными?или
- 3. Повторение. (Устно)Векторы в пространстве.1) Дано: Найти:2) Дано:
- 4. Угол между векторами.ОАВαЕсли
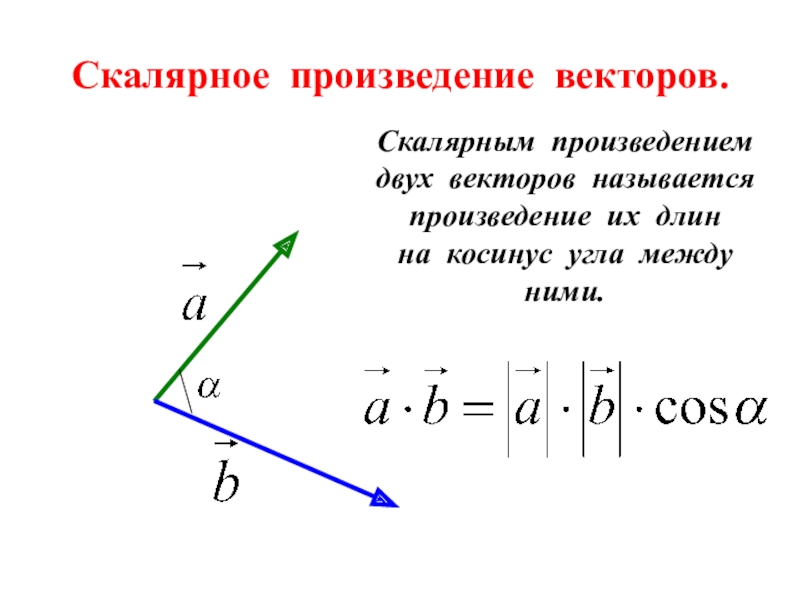
- 5. Скалярное произведение векторов.Скалярным произведением двух векторов называетсяпроизведение их длинна косинус угла междуними.
- 6. Если
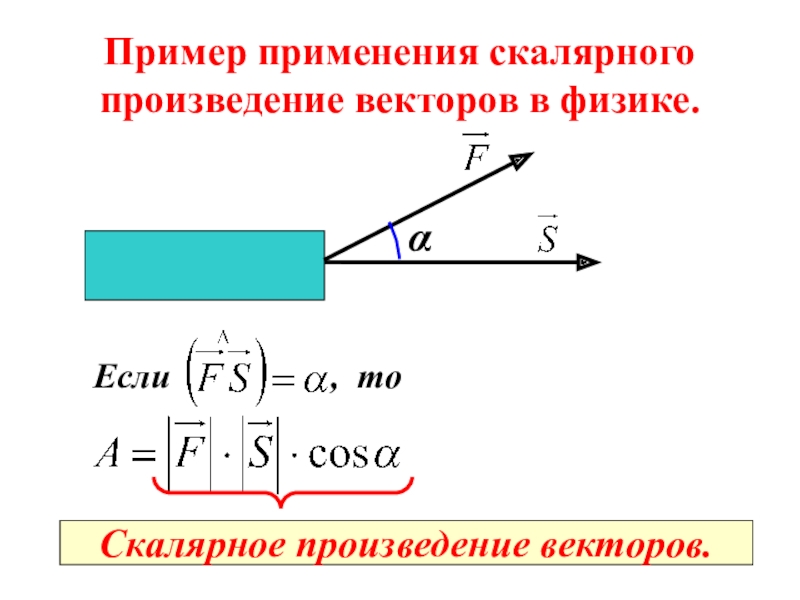
- 7. Пример применения скалярного произведение векторов в физике.αЕсли
- 8. Формула скалярного произведения векторов в пространстве.Скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.
- 9. Косинус угла между ненулевыми векторами
- 10. Скалярное произведение векторов.
- 11. Скачать презентанцию
Повторение:Какие векторы называются равными?Как найти длину вектора по координатам его начала и конца?АВКакие векторы называются коллинеарными?или
Слайды и текст этой презентации
Слайд 2Повторение:
Какие векторы называются равными?
Как найти длину вектора по координатам его
начала и конца?
Слайд 3Повторение. (Устно)
Векторы в пространстве.
1) Дано:
Найти:
2) Дано:
Равны ли векторы
и
?Нет, т.к.равные векторы имеют равные
координаты.
3) Дано:
? Коллинеарны ли векторы и ?
Нет
Слайд 5Скалярное произведение векторов.
Скалярным произведением
двух векторов называется
произведение их длин
на косинус
угла между
ними.
Слайд 6
Если , то
Если
, то
Если
, то
Если
, то
Скалярное произведение
называется
скалярным квадратом вектора
Вспомним планиметрию…
Слайд 7Пример применения скалярного произведение векторов в физике.
α
Если
, то
Скалярное произведение векторов.
Слайд 8Формула скалярного произведения векторов в пространстве.
Скалярное произведение двух векторов равно
сумме произведений соответствующих координат этих векторов.
