Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
УМНОЖЕНИЕ ЧИСЕЛ С ФИКСИРОВАННОЙ ЗАПЯТОЙ 1
Содержание
- 1. УМНОЖЕНИЕ ЧИСЕЛ С ФИКСИРОВАННОЙ ЗАПЯТОЙ 1
- 2. Умножение чисел с фиксированной запятой, заданных в прямом коде
- 3. Xпк = Зн Х.|Х|Yпк = ЗнY.|Y| =
- 4. |Z| = |Х| * |Y| =
- 5. Исходное число:Результат:
- 6. Исходное число:
- 7. Умножение чисел с фиксированной запятой, заданных в дополнительном коде
- 8. Умножение чисел с фиксированной запятой с
- 9. Умножение чисел с фиксированной запятой со
- 10. Исходное число:Результат:
- 11. Исходное число:
- 12. ДЕЛЕНИЕ ЧИСЕЛ С ФИКСИРОВАННОЙ ЗАПЯТОЙ
- 13. Деление чисел с фиксированной запятой, заданных в прямом коде
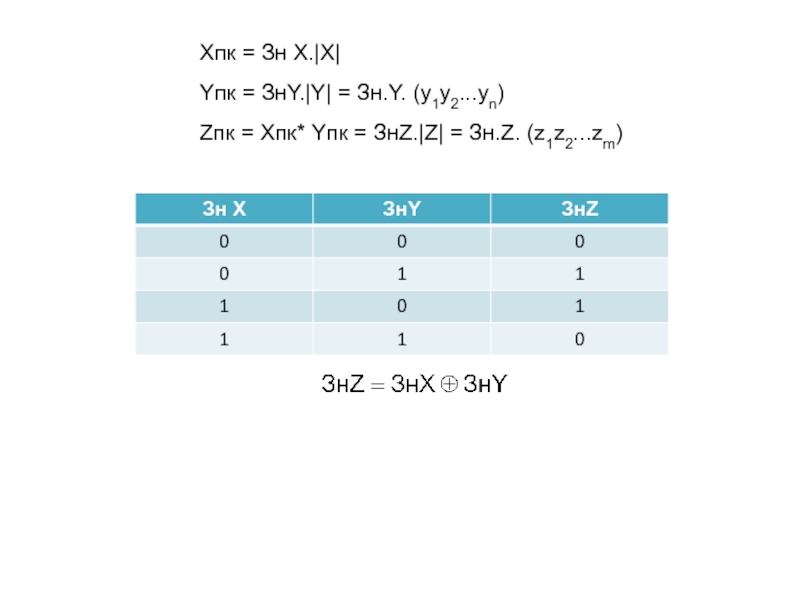
- 14. Xпк = Зн Х.|Х|Yпк = ЗнY.|Y|Zпк =
- 15. Деление чисел с фиксированной запятой, заданных
- 16. α0 = |X| - |Y|Если α0 ≥
- 17. Деление чисел с фиксированной запятой, заданных
- 18. α0 = |X| - |Y|Если α0 ≥
- 19. Деление чисел с фиксированной запятой, заданных в дополнительном коде
- 20. Деление чисел с фиксированной запятой, заданных
- 21. Деление чисел с фиксированной запятой, заданных
- 22. Скачать презентанцию
Умножение чисел с фиксированной запятой, заданных в прямом коде
Слайды и текст этой презентации
Слайд 4|Z| = |Х| * |Y| = |Х| *(y12-1+ y22-2
+...+ yn2-n ) =
=|Х| y1 * 2-1+ |Х| y2 2-2
+... +|Х| yn-1 2-n-1+ |Х| yn 2-n = (1)= ((...((0+ |Х| yn) *2-1 +|Х| yn-1) *2-1 + ... + |Х| y2) *2-1 + y1 |Х|) *2-1 (2)
Формула (1) – описывает умножение со старших разрядов множи-теля, а формула (2) – с младших разрядов:
Ai = Ai-12-1 + |X| yn+1-i
An = |X| * |Y| =|Z|
Слайд 8Умножение чисел с фиксированной запятой с младших разрядов в дополнительном
коде
Алгоритм.
[Z]дк = (…(0+[X]дк*[yn+1 – yn])*2-1 + [X]дк*[yn – yn-1])*2-1 +…+
+
[X]дк*[y2 – y1])*2-1 + [X]дк*[y1 – y0]Если yi = yi+1, то производится сдвиг частичного произведения.
Если yi = 0 и yi+1 = 1, то к частичному произведению прибавляется [X]дк
Если yi = 1 и yi+1 = 0, то к частичному произведению прибавляется [-[X]дк] дк.
В качестве y0 берётся знак числа.
yn+1 ≡ 0
Слайд 9Умножение чисел с фиксированной запятой со старших разрядов в дополнительном
коде
Алгоритм:
[Z]дк = [X]дк * [Y]дк = [X]дк * (y1 –
y0) + [X]дк * (y2 – y1)*2-1 + … +
+ [X]дк * (yn+1 – yn)*2-nЕсли yk = 0 и yk-1 = 1, то к частичному произведению прибавляется [X]дк, сдвинутый на k разрядов вправо
Если yk = 1 и yk-1 = 0, то к частичному произведению прибавляется [-[X]дк] дк, сдвинутый на k разрядов вправо
Если yk = yk-1, то на этом шаге [X]дк не участвует в формировании произведения.
В качестве y0 берётся знак числа.
yn+1 ≡ 0.






![УМНОЖЕНИЕ ЧИСЕЛ С ФИКСИРОВАННОЙ ЗАПЯТОЙ
1 Умножение чисел с фиксированной запятой с младших разрядов в дополнительном кодеАлгоритм.[Z]дк Умножение чисел с фиксированной запятой с младших разрядов в дополнительном кодеАлгоритм.[Z]дк = (…(0+[X]дк*[yn+1 – yn])*2-1 +](/img/thumbs/8b29a52cf3fd53529f9163ab2487db21-800x.jpg)
![УМНОЖЕНИЕ ЧИСЕЛ С ФИКСИРОВАННОЙ ЗАПЯТОЙ
1 Умножение чисел с фиксированной запятой со старших разрядов в дополнительном кодеАлгоритм:[Z]дк Умножение чисел с фиксированной запятой со старших разрядов в дополнительном кодеАлгоритм:[Z]дк = [X]дк * [Y]дк =](/img/thumbs/c27db13bff5a2cbdc76f089399c12393-800x.jpg)