Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
Содержание
- 1. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
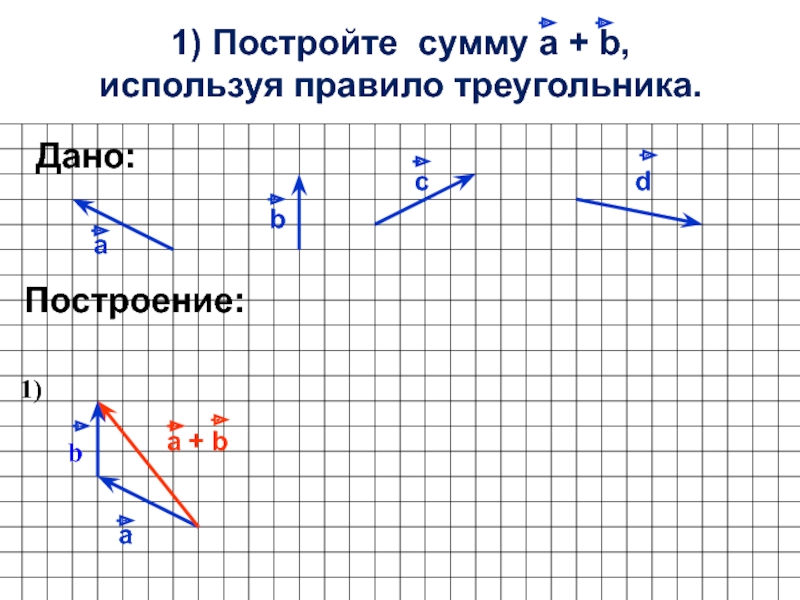
- 2. 1) Постройте сумму а + b, используя правило треугольника.аbcПостроение:dДано:аb1)a + b
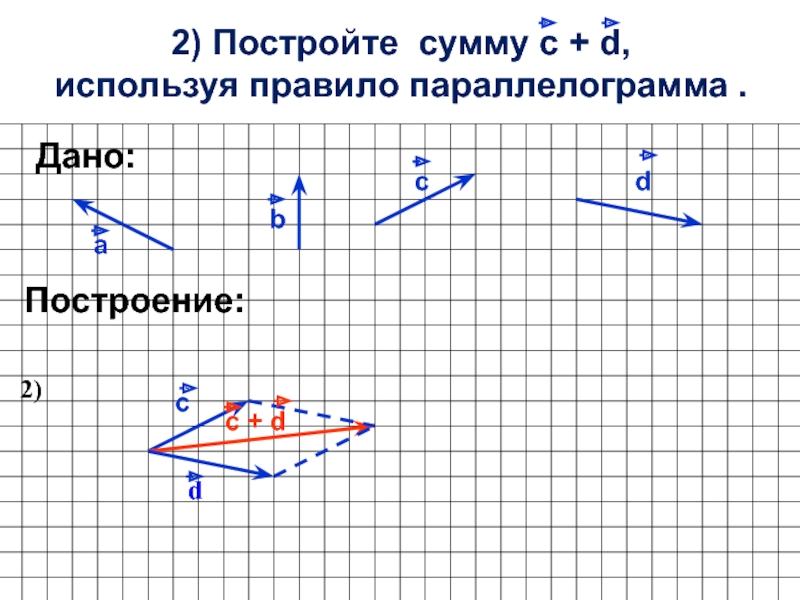
- 3. 2) Постройте сумму с + d, используя правило параллелограмма .аbcПостроение:dДано:сd2)c + d
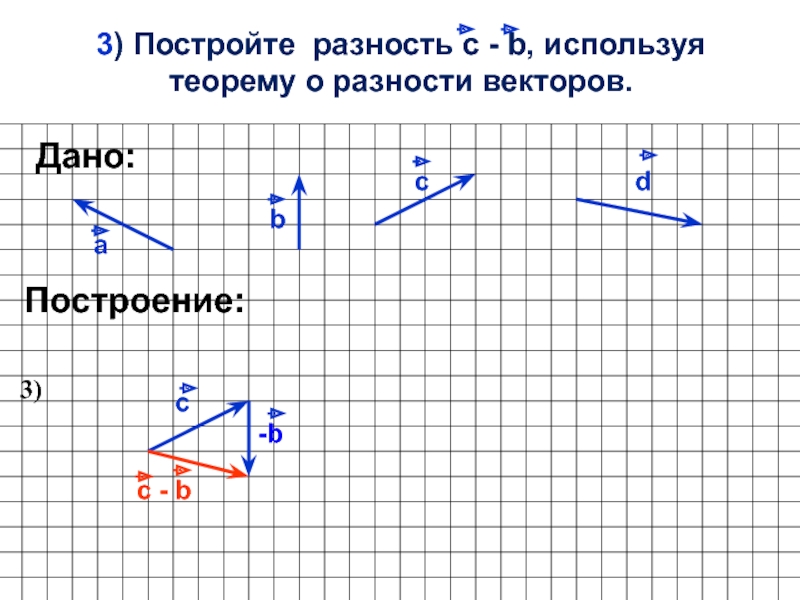
- 4. 3) Постройте разность с - b, используя теорему о разности векторов.аbcПостроение:dДано:с-b3)с - b
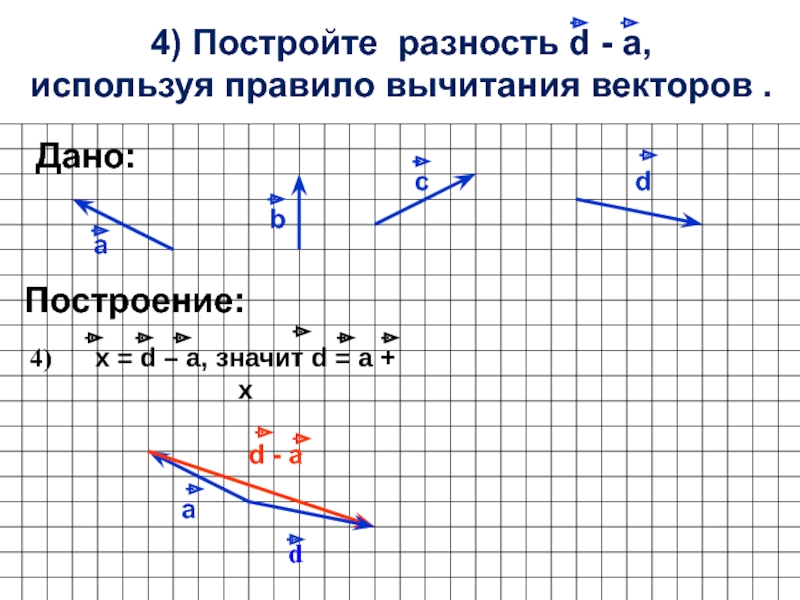
- 5. 4) Постройте разность d - а, используя
- 6. 5) Упростите выражение:1 вариант. CA – OB
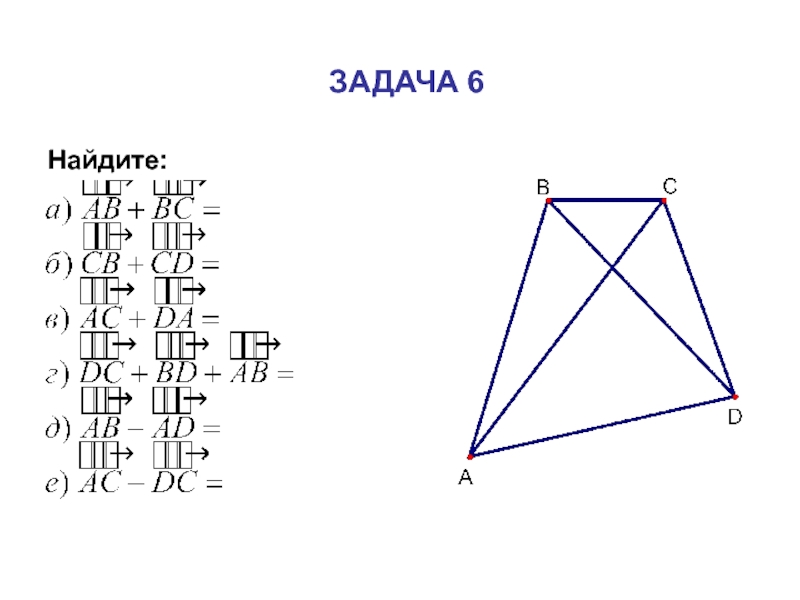
- 7. ЗАДАЧА 6Найдите:
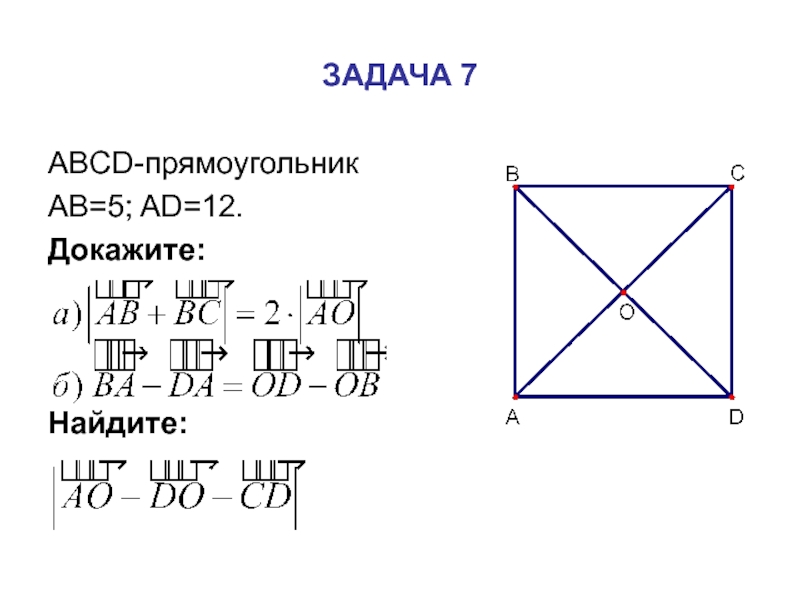
- 8. ЗАДАЧА 7ABCD-прямоугольникAB=5; AD=12.Докажите:Найдите:
- 9. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
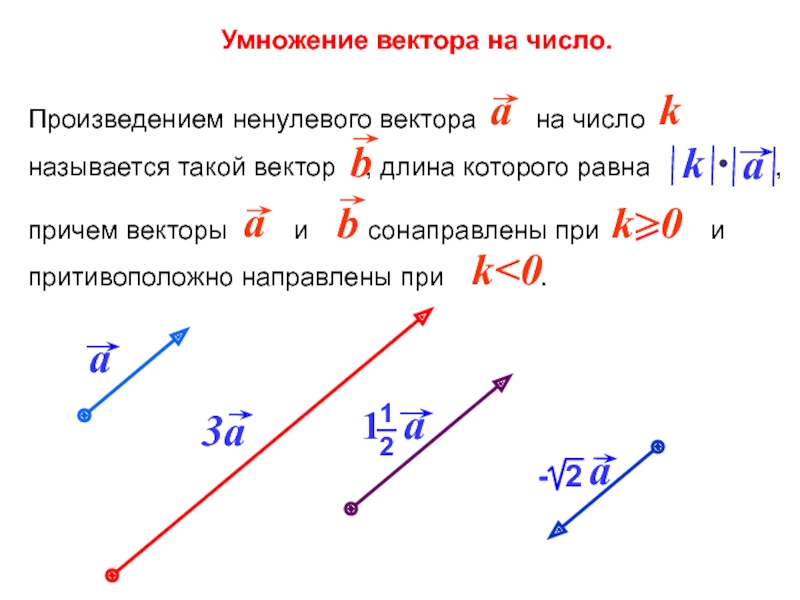
- 10. Умножение вектора на число.
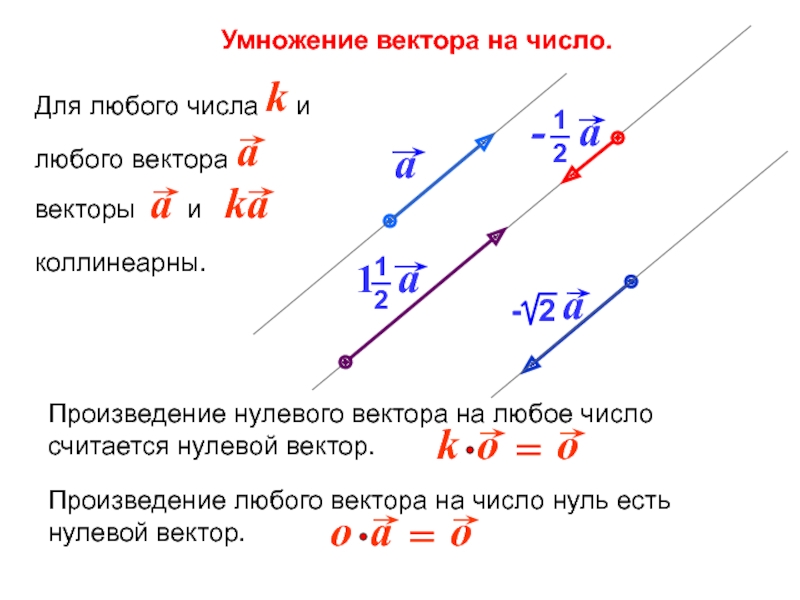
- 11. Умножение вектора на число.
- 12. Умножение вектора на число.Произведение любого вектора на
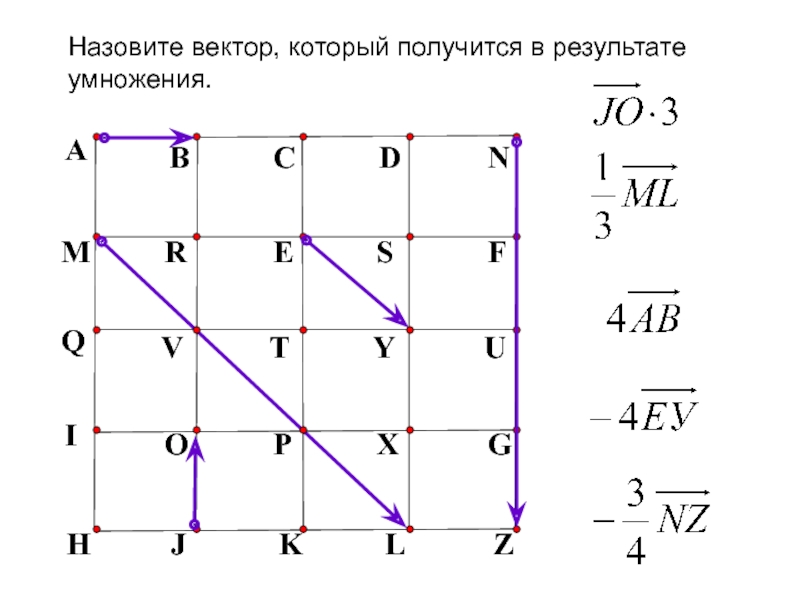
- 13. ABCDNMRESFHJKLZQVTYUНазовите вектор, который получится в результате умножения.IOPXG
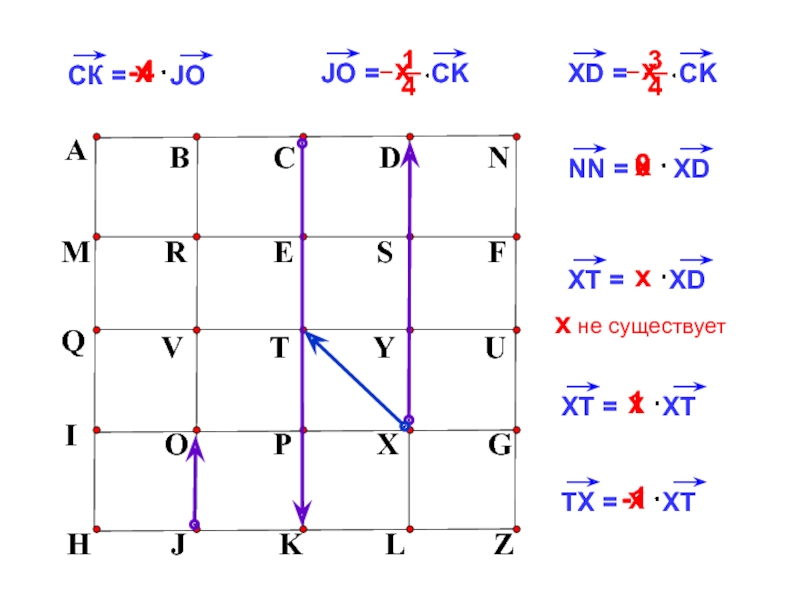
- 14. х-40хABCDNMRESFHJKLZQVTYUIOPXGххххх не существует1х-1
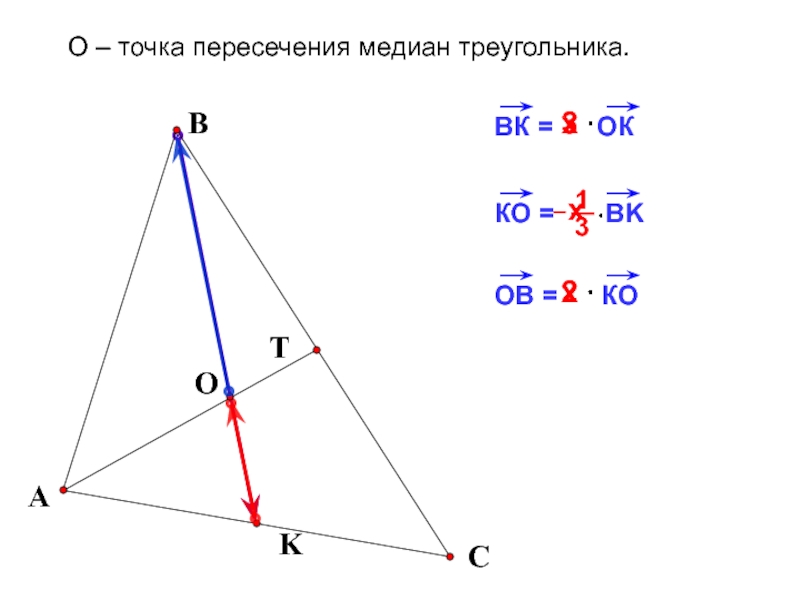
- 15. 2х3ACOKTBО – точка пересечения медиан треугольника.хх
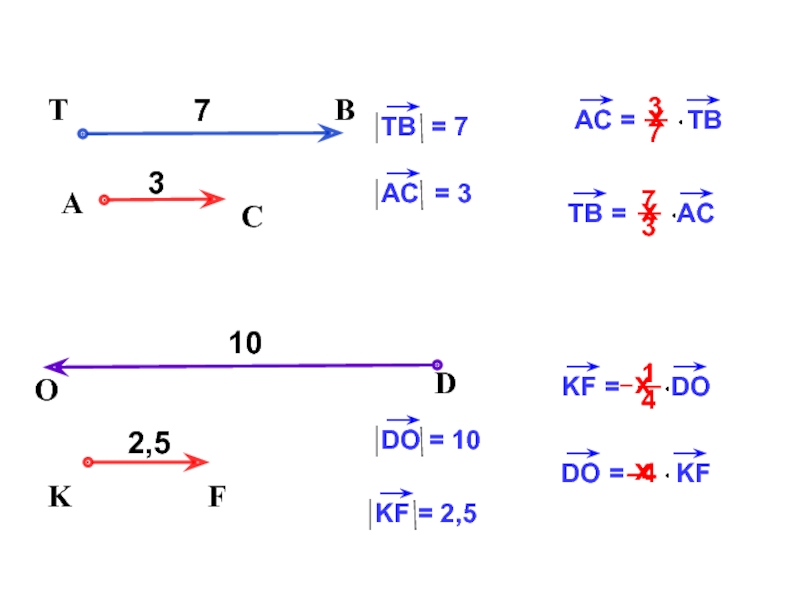
- 16. х –4AC7TBх3хх
- 17. х1,25ACTBТВ = АСхДлина вектора TB на 25% больше длины вектора АС-0,75
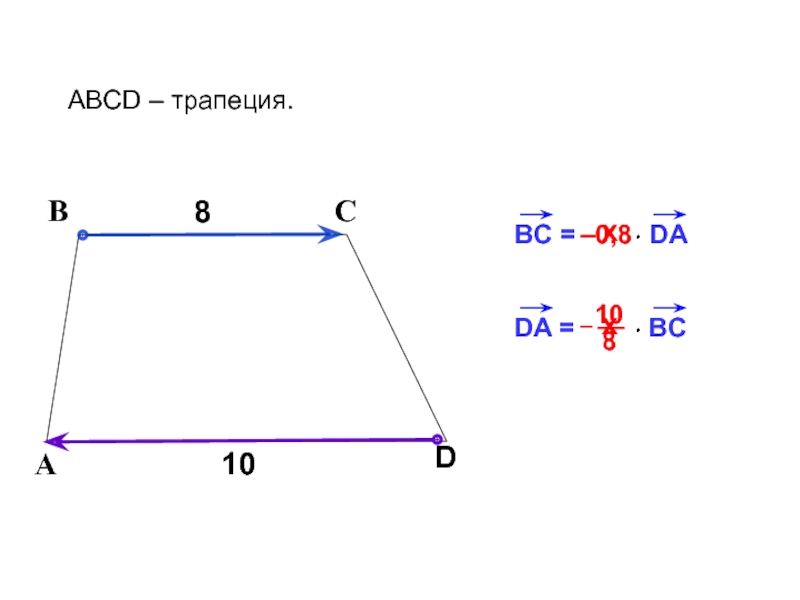
- 18. BC = DA8ВСABCD – трапеция.АD10х –0,8DA = BCх
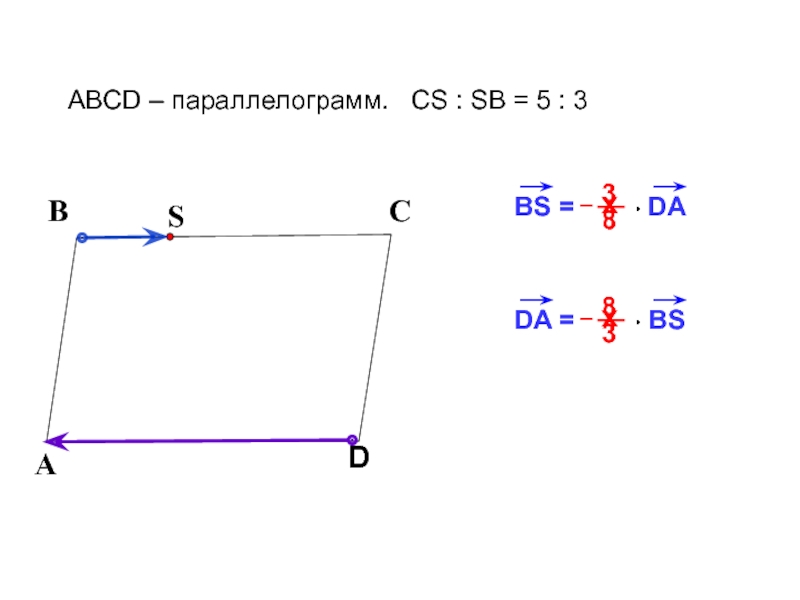
- 19. ВСABCD – параллелограмм. CS : SB
- 20. Умножение вектора на число обладает следующими основными свойствами.Сочетательный законПервый распределительный законВторой распределительный закон123
- 21. Рисунок иллюстрирует сочетательный закон. Представлен случай, когда k = 2, l = 3.Сочетательный закон1BO
- 22. BРисунок иллюстрирует первый распределительный закон. Представлен случай,
- 23. OВторой распределительный закон3AРисунок иллюстрирует второй распределительный закон.
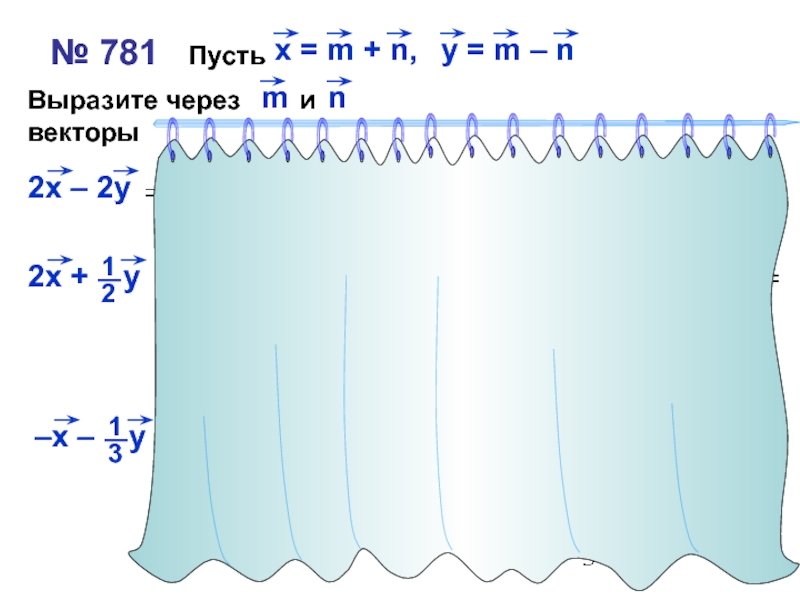
- 24. № 781 Пусть Выразите
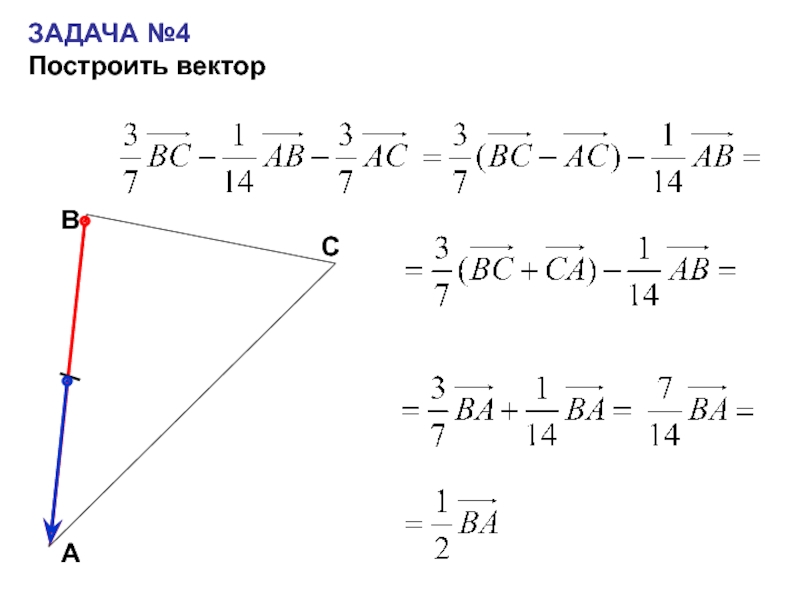
- 25. ЗАДАЧА №4Построить векторСАВ
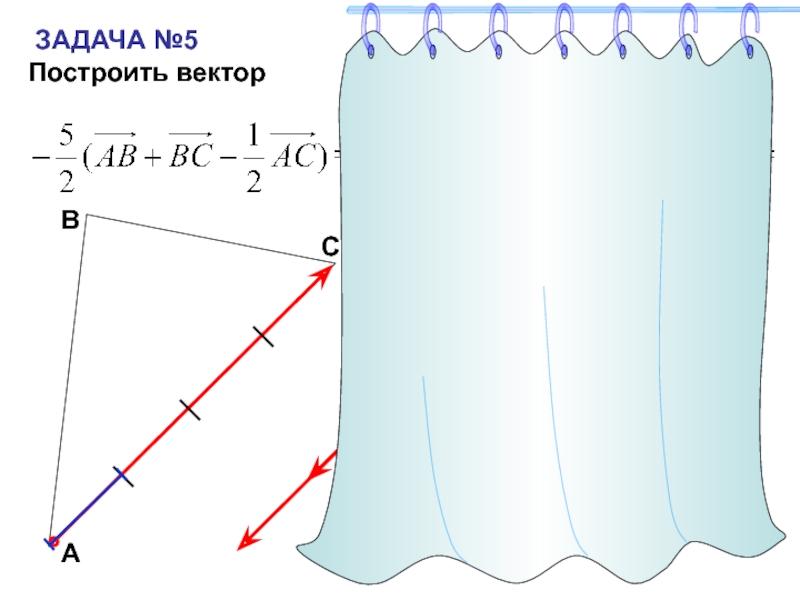
- 26. ЗАДАЧА №5Построить векторСАВ
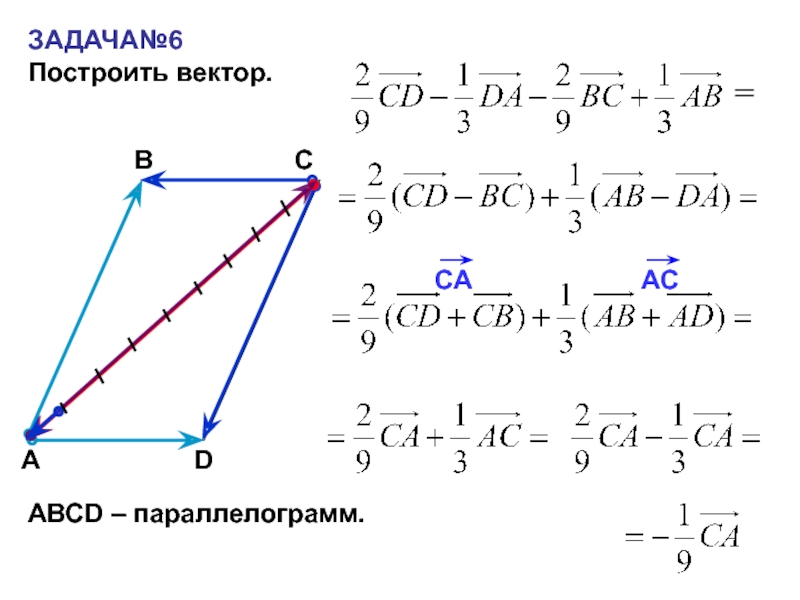
- 27. ЗАДАЧА№6Построить вектор.САВ=АВСD – параллелограмм. D
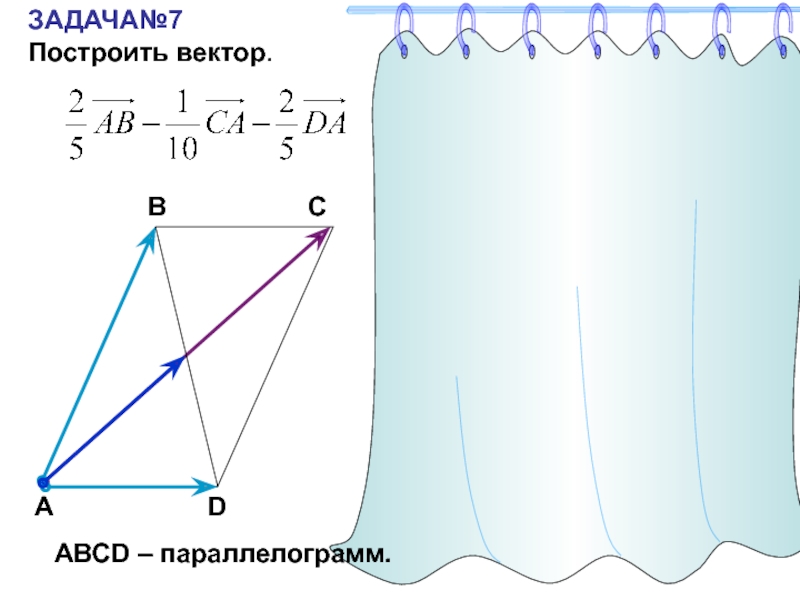
- 28. ЗАДАЧА№7Построить вектор.САВDАВСD – параллелограмм.
- 29. АВСD – ромб. Е ВС, ВЕ
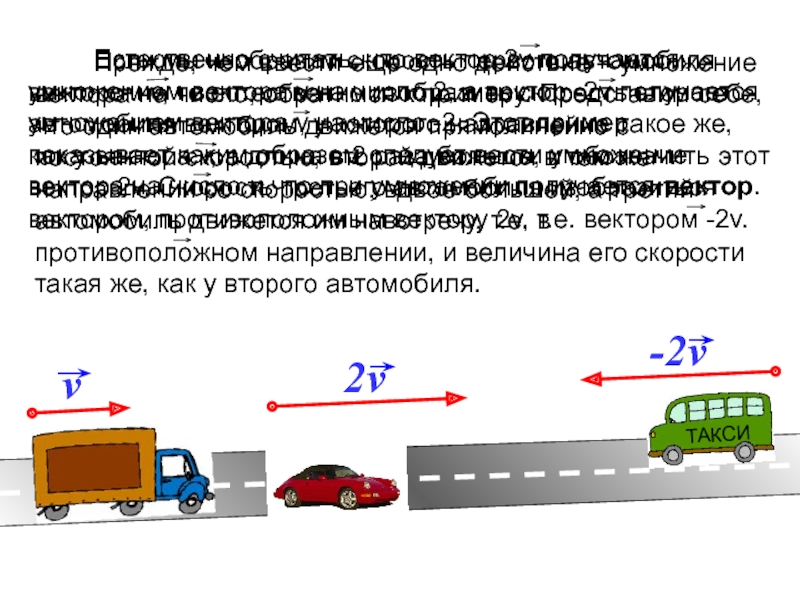
- 30. Прежде, чем ввести
- 31. Скачать презентанцию
1) Постройте сумму а + b, используя правило треугольника.аbcПостроение:dДано:аb1)a + b
Слайды и текст этой презентации
Слайд 54) Постройте разность d - а,
используя правило вычитания векторов
.
а
b
c
Построение:
d
Дано:
а
d
4)
х = d – a, значит d = а +
х d - a
Слайд 65) Упростите выражение:
1 вариант.
CA – OB – CD +
AB =
2 вариант.
BA + CD – OD – CA =
= CA + BO + DC + AB =
= DC + CA + AB + BO =
= DO.
= BA + CD + DO + AC =
= BA + AC + CD + DO =
= BO.
Слайд 12Умножение вектора на число.
Произведение любого вектора на число нуль есть
нулевой вектор.
Произведение нулевого вектора на любое число считается нулевой вектор.
Слайд 20Умножение вектора на число обладает следующими основными свойствами.
Сочетательный закон
Первый распределительный
закон
Второй распределительный закон
1
2
3
Слайд 21Рисунок иллюстрирует сочетательный закон. Представлен случай, когда k =
2, l = 3.
Сочетательный закон
1
B
O
Слайд 22B
Рисунок иллюстрирует первый распределительный закон. Представлен случай, когда k
= 3, l = 2.
O
Первый распределительный закон
2
OB =
Слайд 23O
Второй распределительный закон
3
A
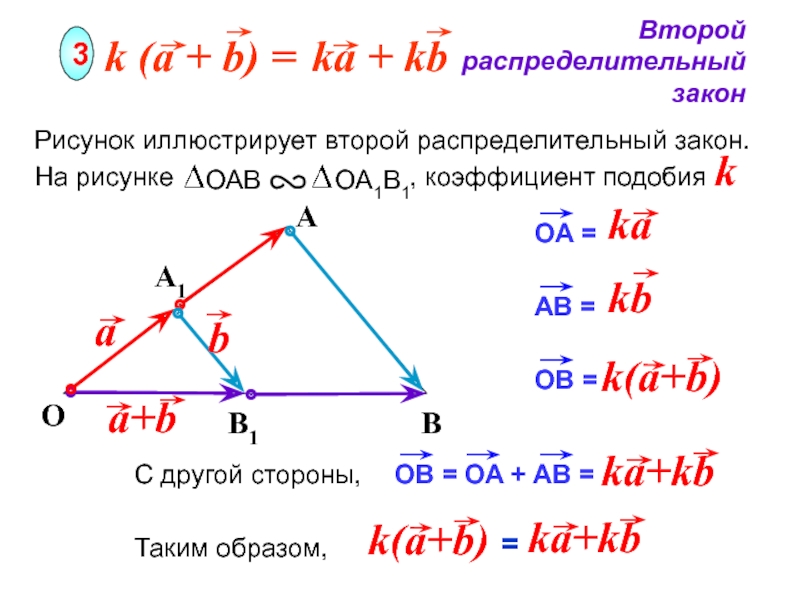
Рисунок иллюстрирует второй распределительный закон.
На рисунке
, коэффициент подобия
k
A1
B1
B
С другой стороны,
Таким образом,
=
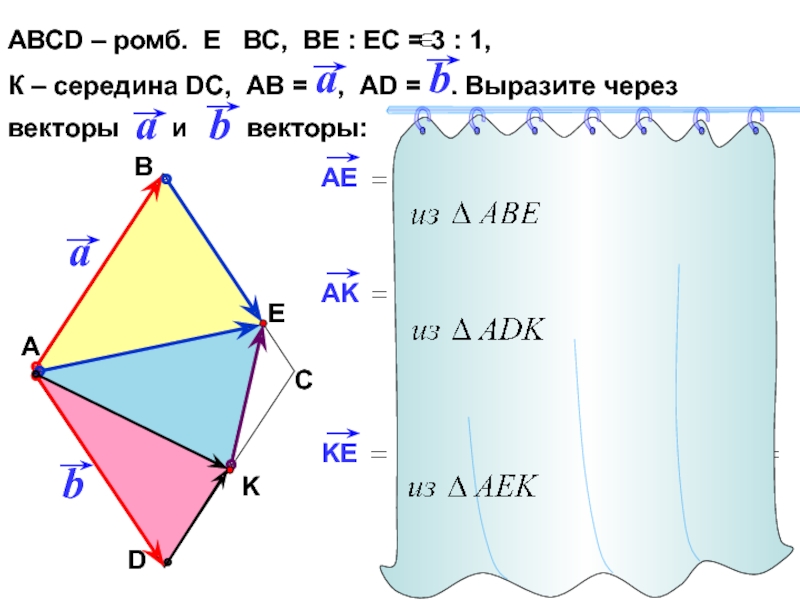
Слайд 29АВСD – ромб. Е ВС, ВЕ : ЕС =
3 : 1,
К – середина DC, АВ =
, AD = . Выразите через векторы и векторы:
С
А
В
D