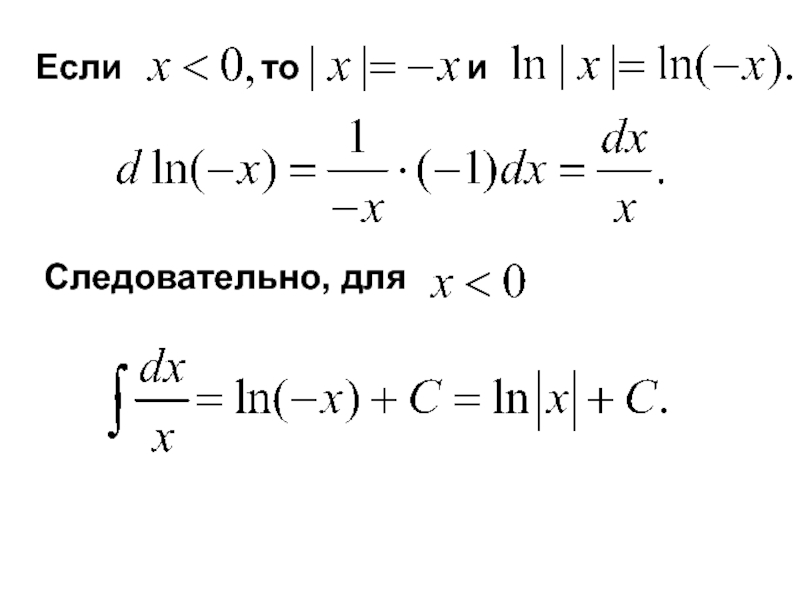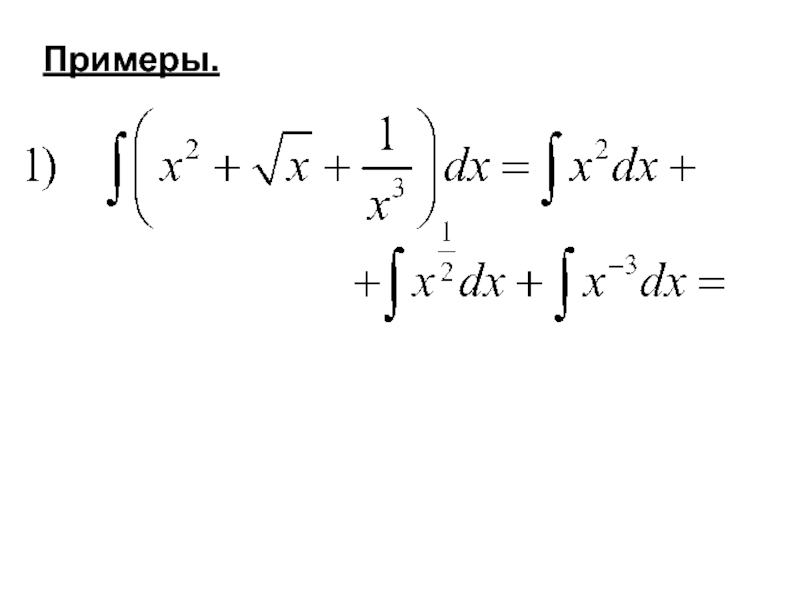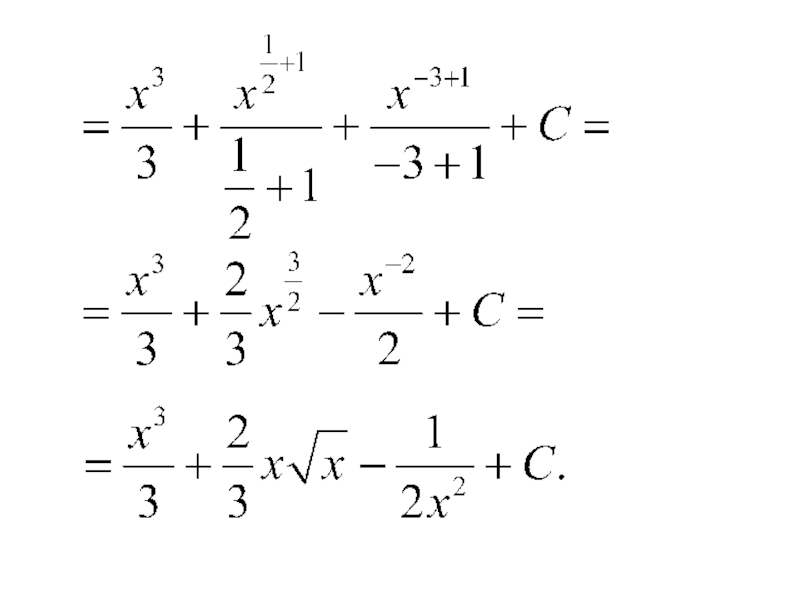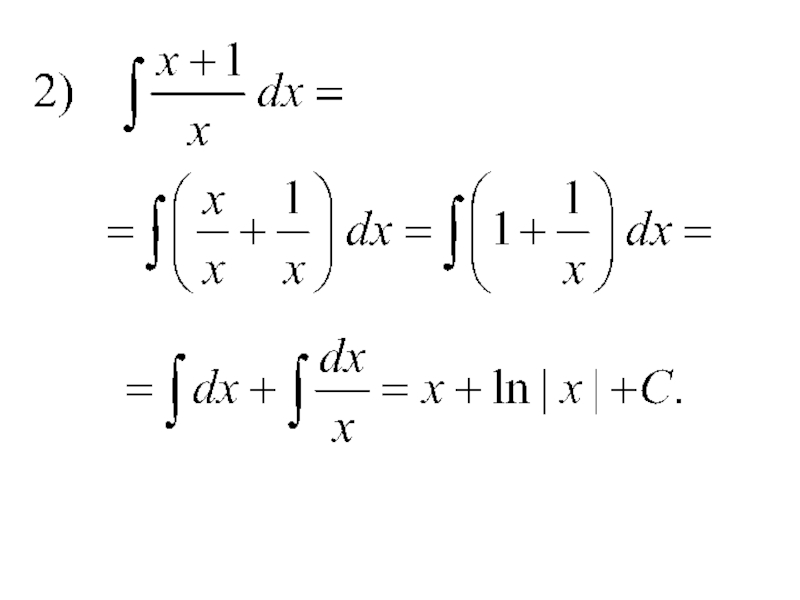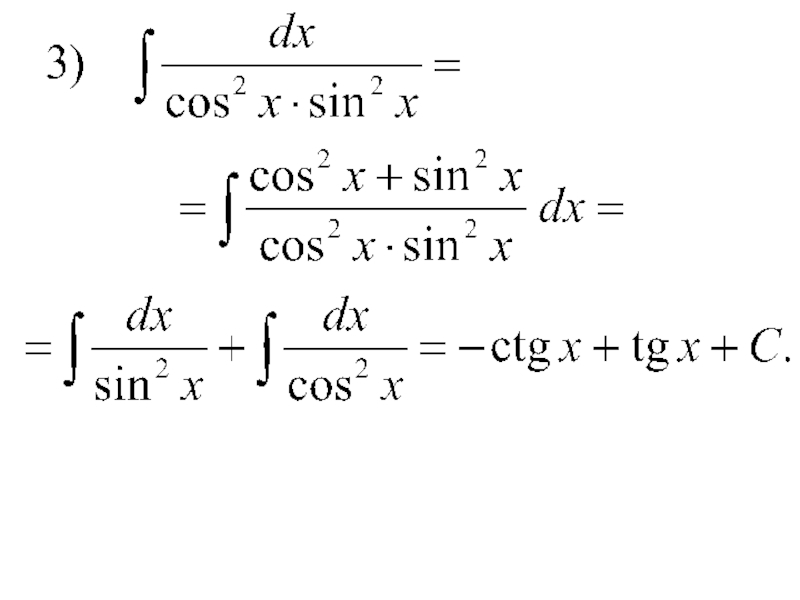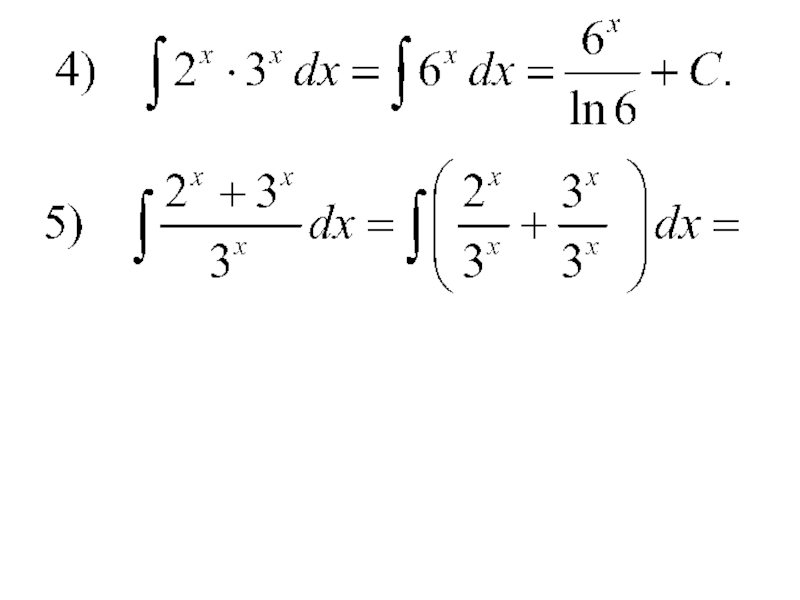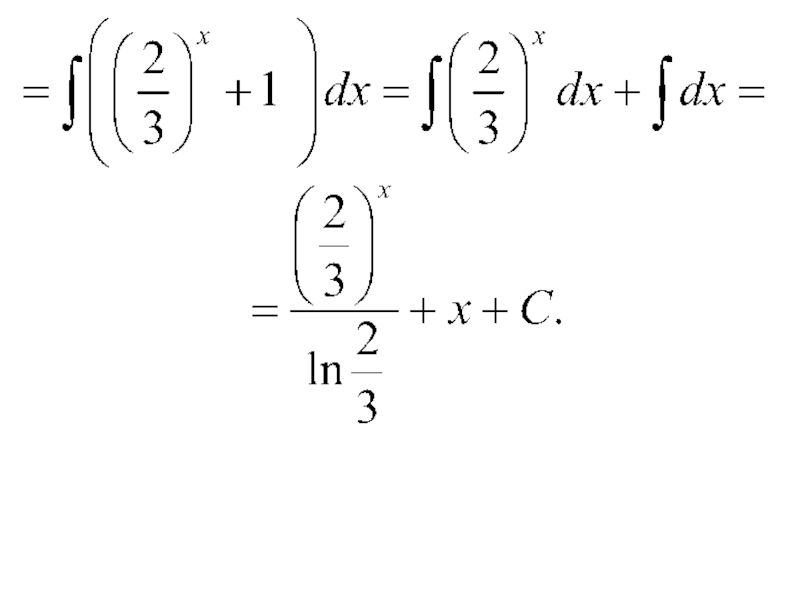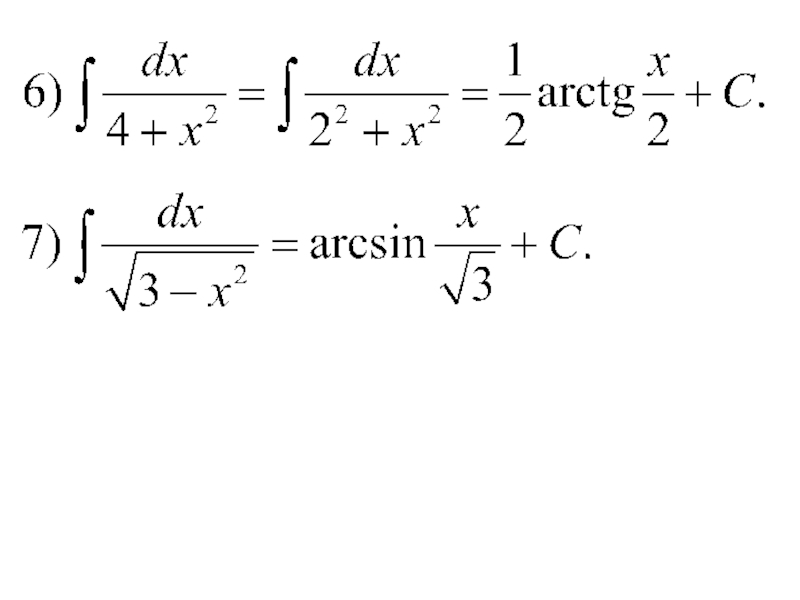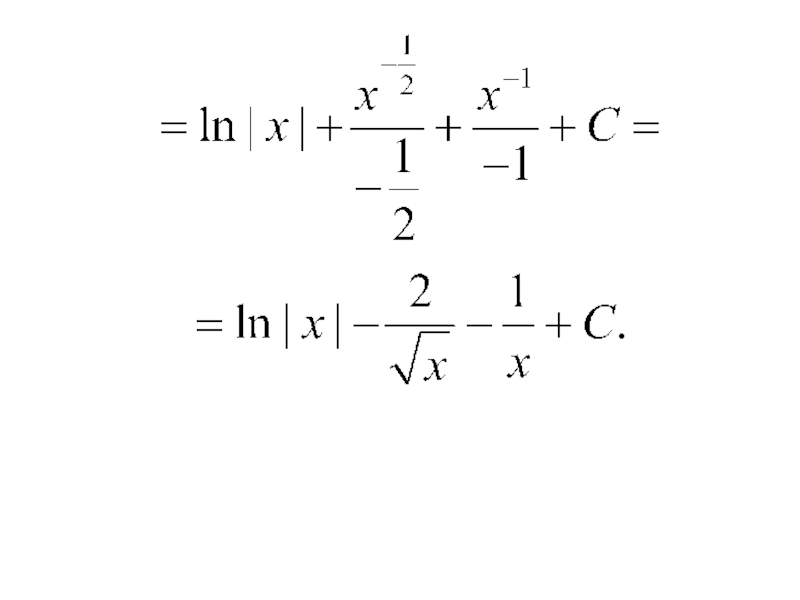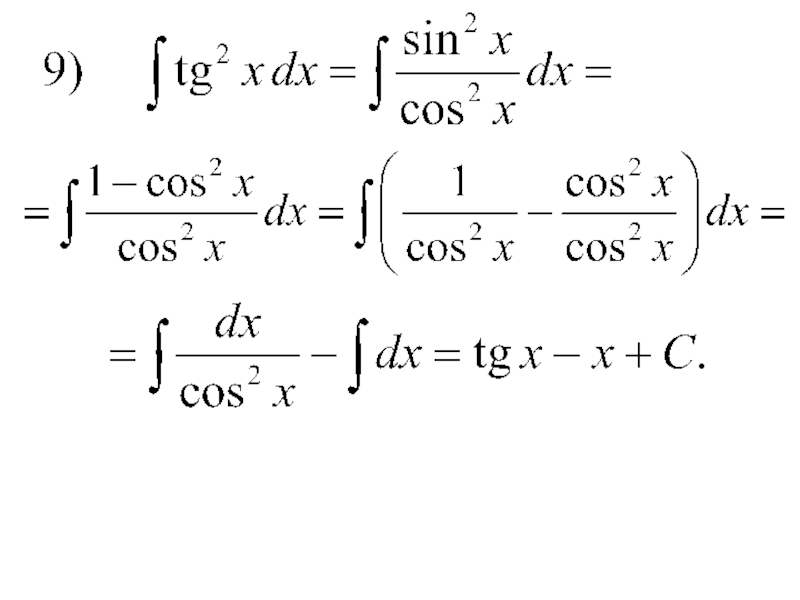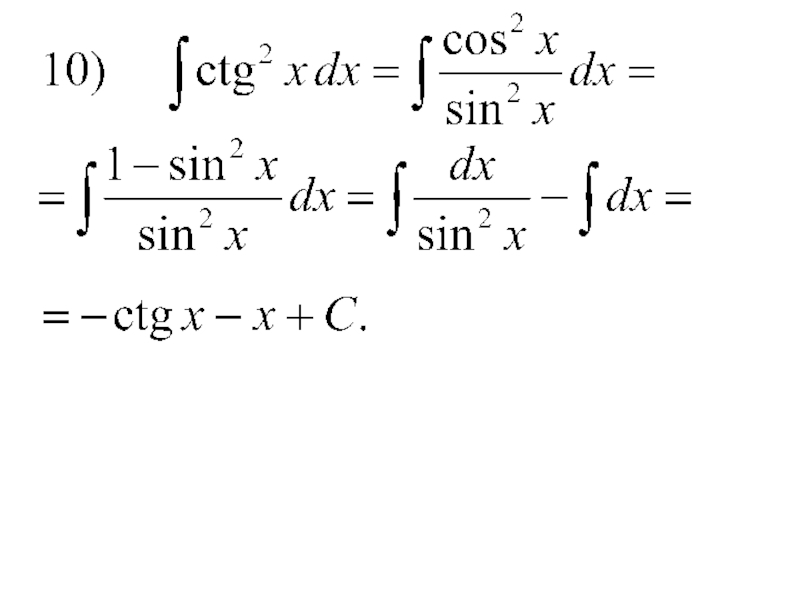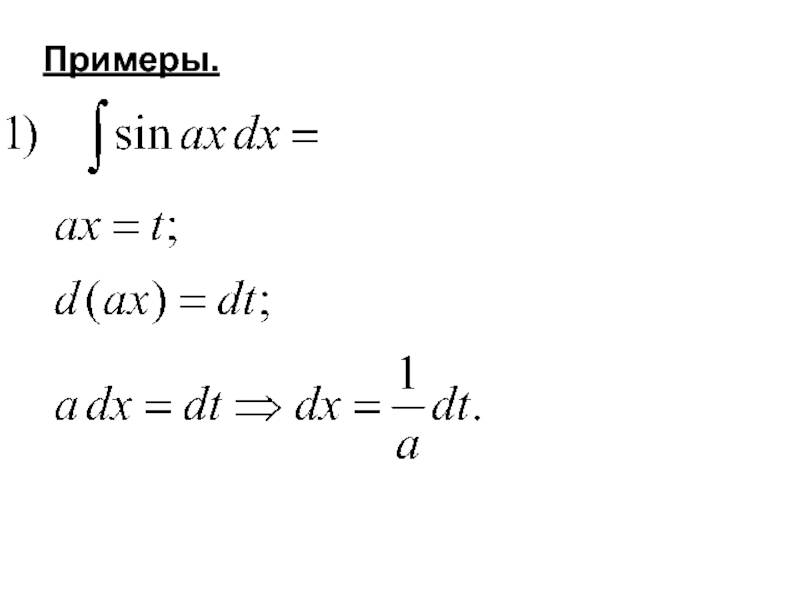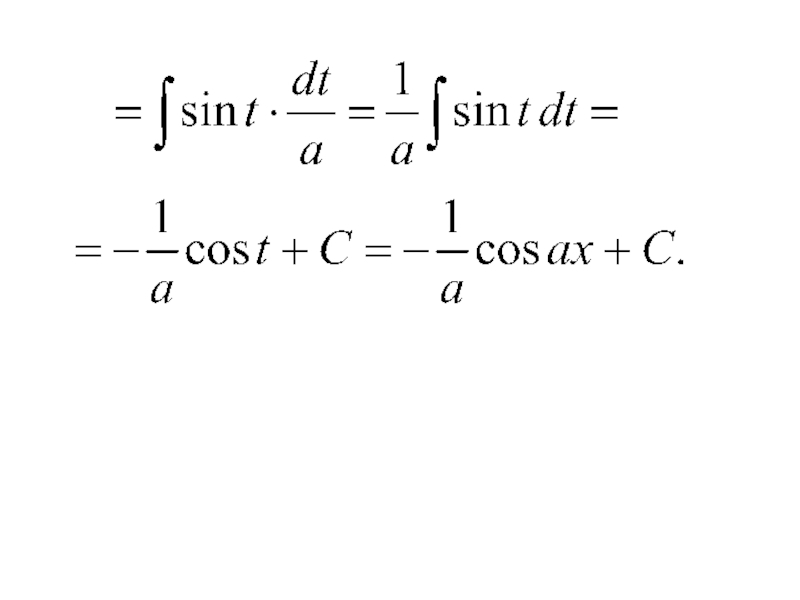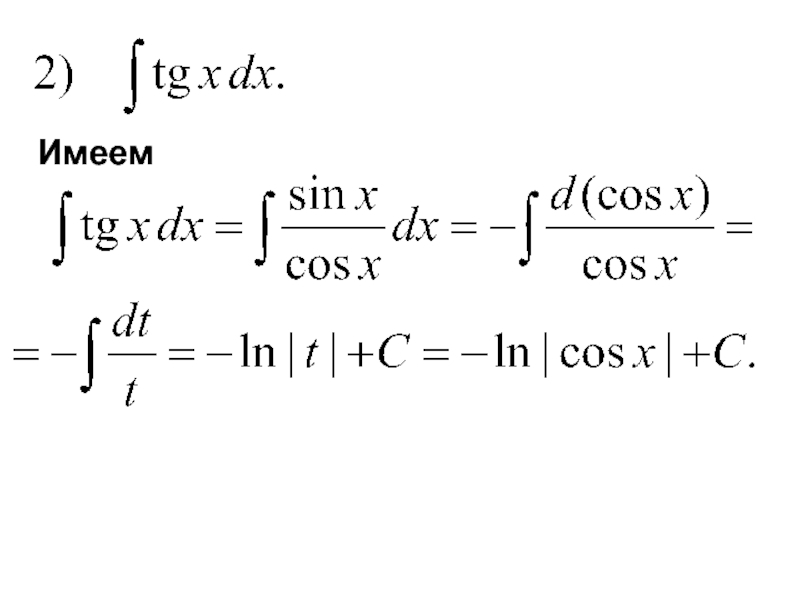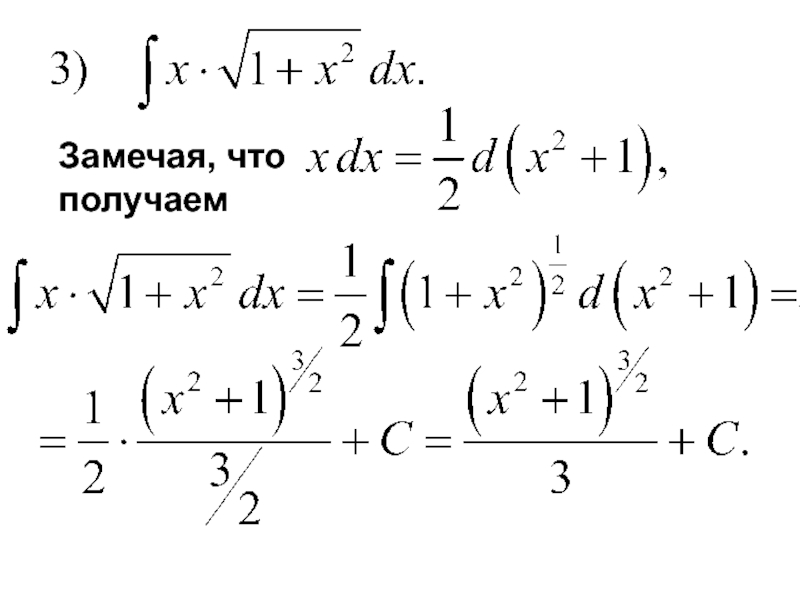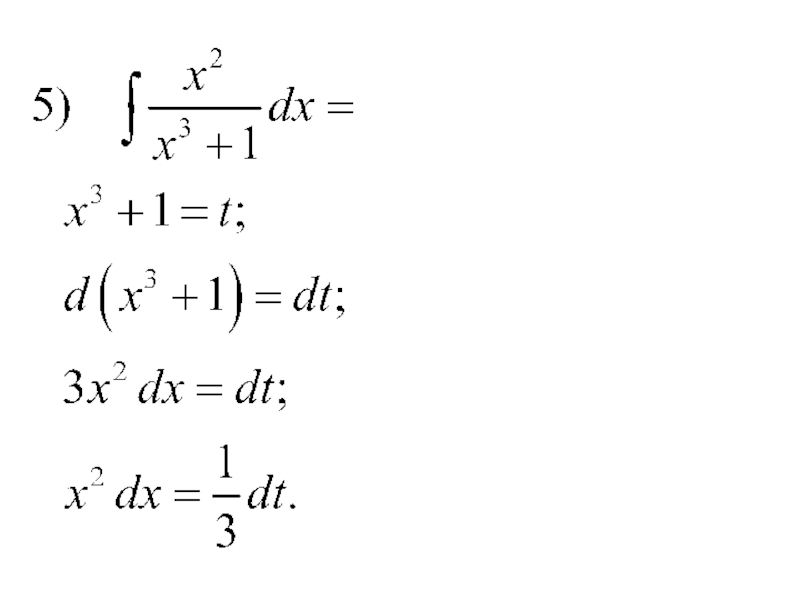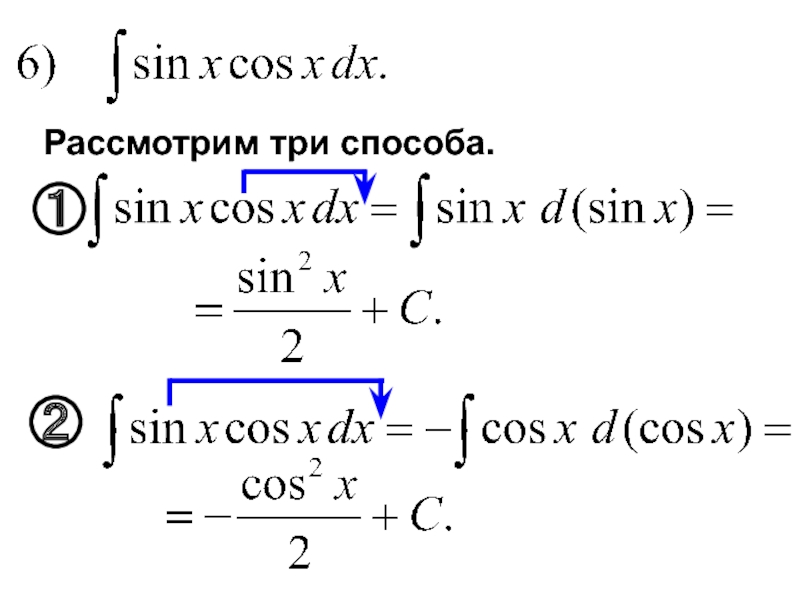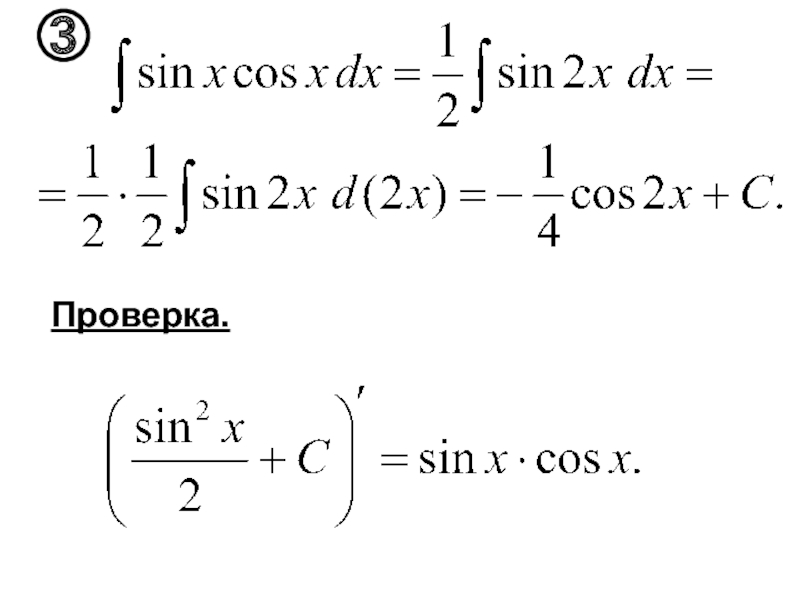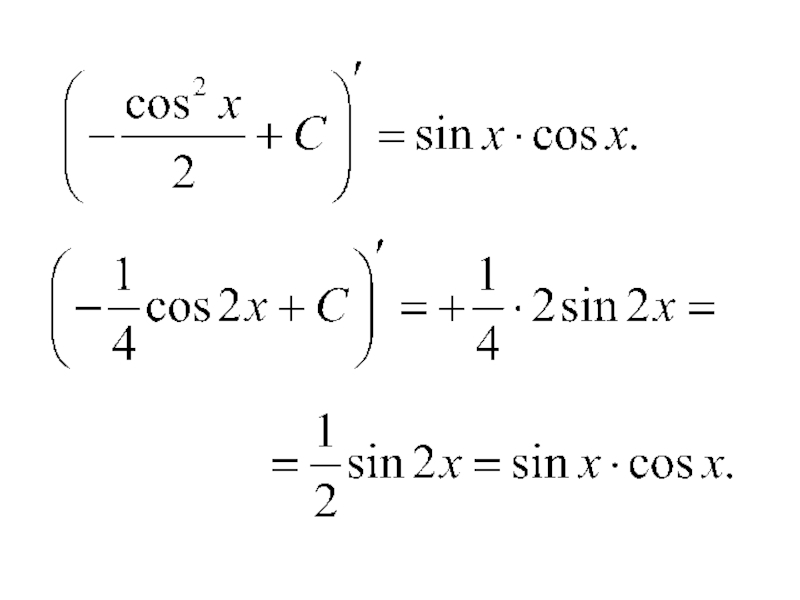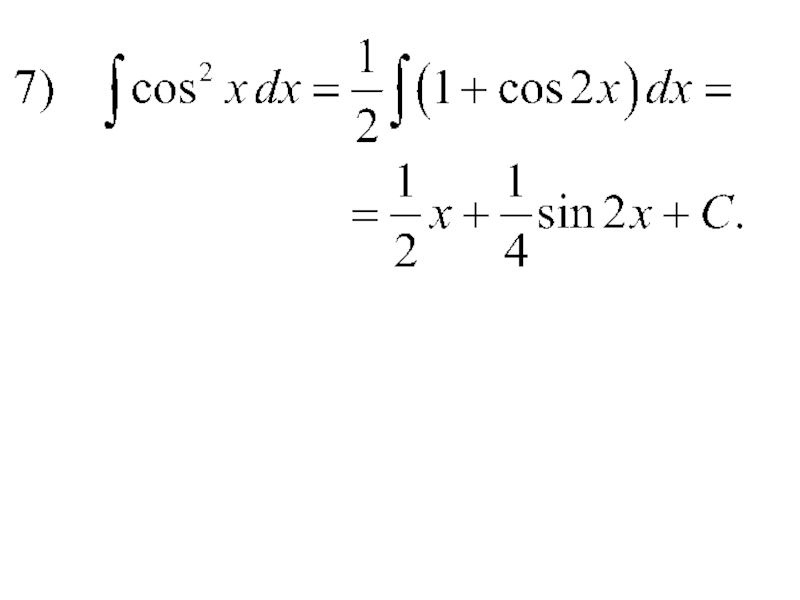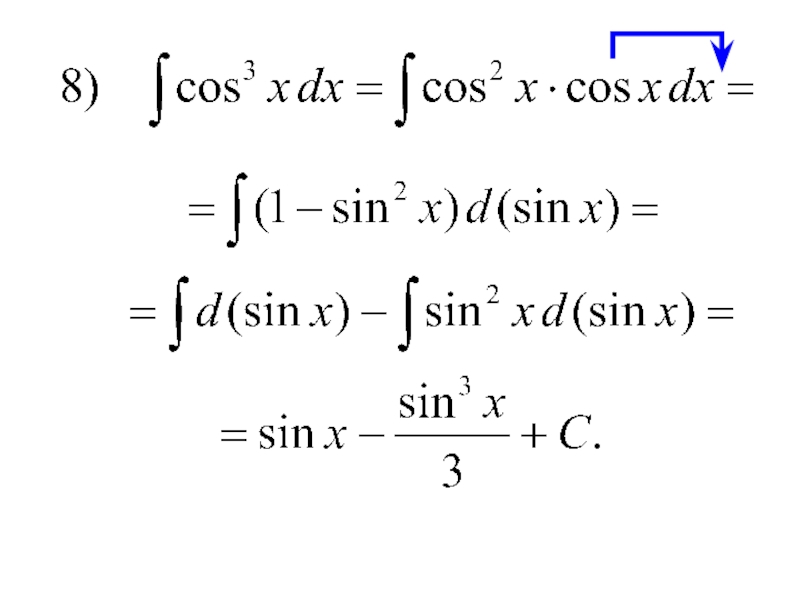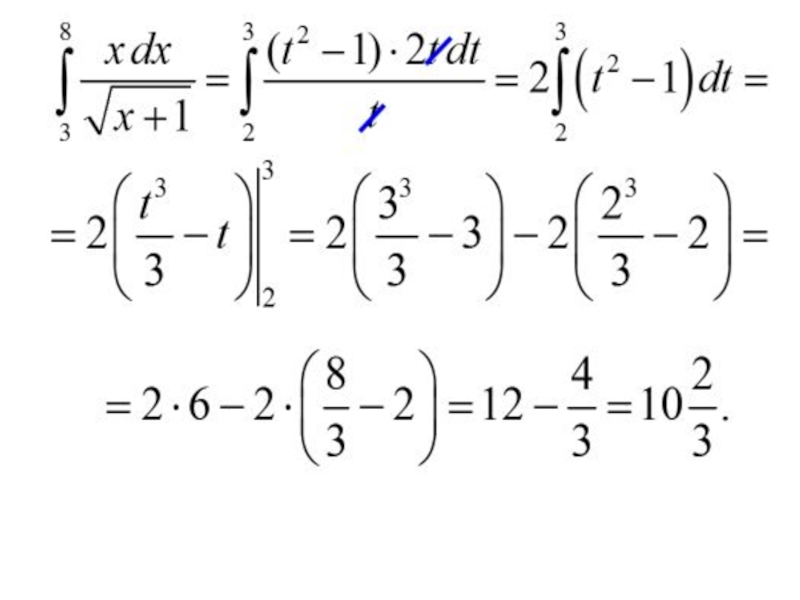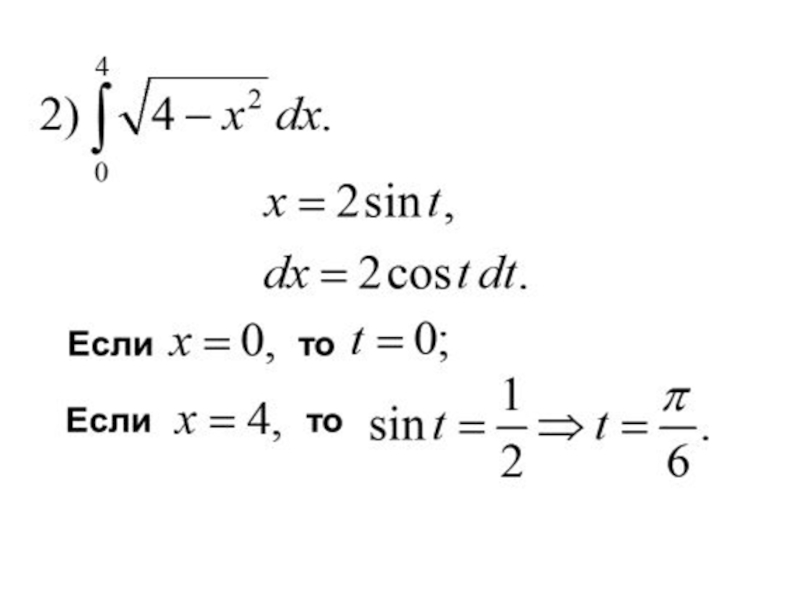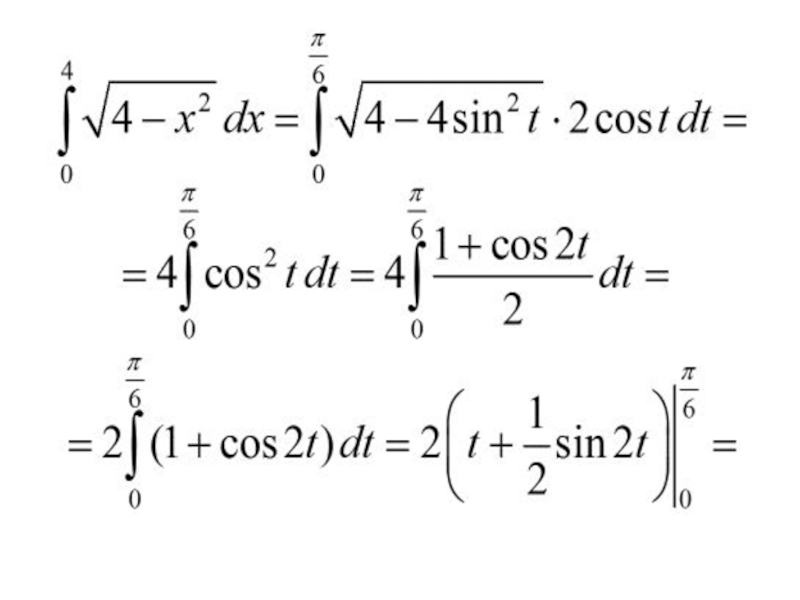Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Управление социальными системами 8. Интегральное исчисление функций одной
Содержание
- 1. Управление социальными системами 8. Интегральное исчисление функций одной
- 2. Раздел 8.Интегральное исчисление функций одной переменной. Орлик Л.К.
- 3. Слайд 3
- 4. Ранее мы по данной функции вычисляли ее
- 5. Определение. Функция
- 6. Таким образом,
- 7. Здесь
- 8. Слайд 8
- 9. Таблица основных интегралов
- 10. Таблица основных интегралов
- 11. Таблица основных интегралов
- 12. Таблица основных интегралов
- 13. Таблица основных интегралов
- 14. Если
- 15. Если
- 16. Примеры.
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
- 27. Теорема. Любая непрерывная на отрезке функция имеет
- 28. Назовем график первообразной функции от
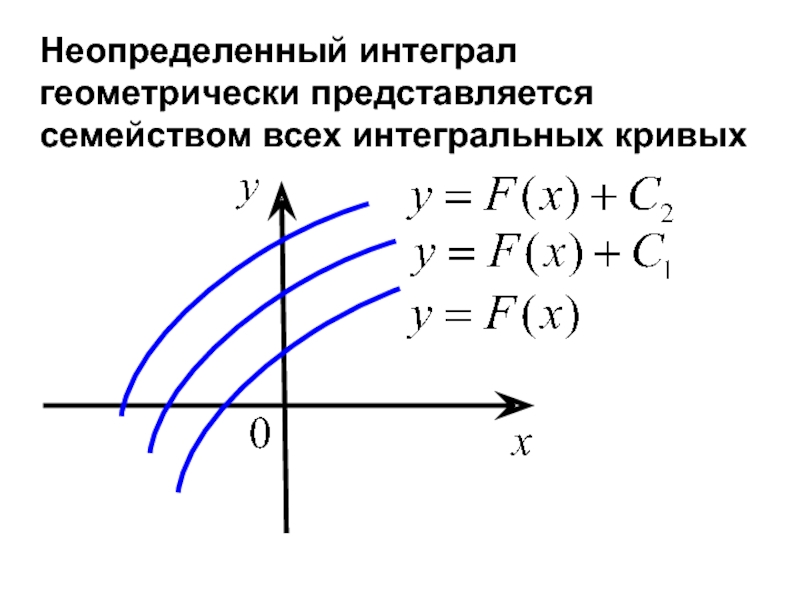
- 29. Неопределенный интеграл геометрически представляется семейством всех интегральных кривых
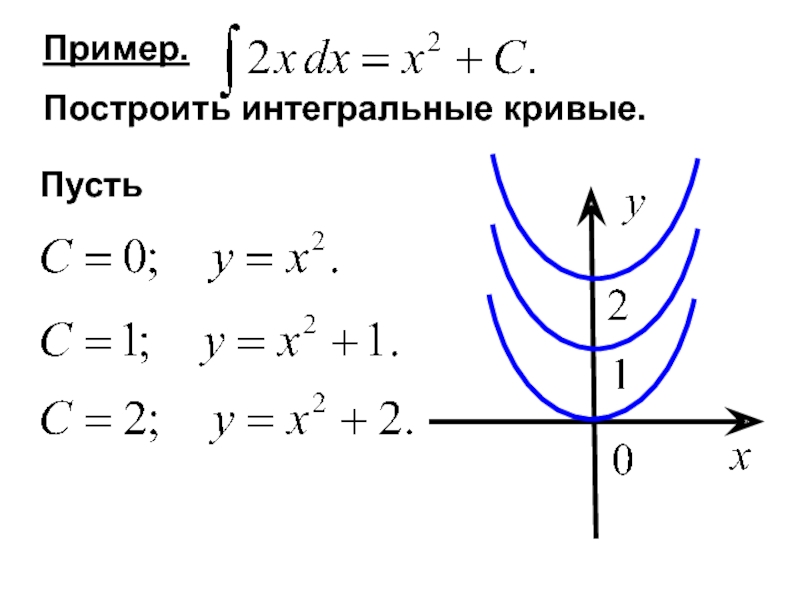
- 30. Пример. Построить интегральные кривые.
- 31. В дифференциальном исчислении производная от любой элементарной
- 32. Можно привести примеры элементарных функций, первообразные от
- 33. Несмотря на это, все эти первообразные хорошо
- 34. Эта функция встречается в теории вероятностей и
- 35. Учебный вопрос 8.2. Методы интегрирования
- 36. Тема: Замена переменной в неопределенном интеграле
- 37. Введем вместо новую переменную связанную с соотношениемТогда
- 38. Примеры.
- 39. Слайд 39
- 40. Имеем
- 41. Здесь мы устно ввели под знак интеграла функцию Заметим, что
- 42. Замечая, что
- 43. 4) Интегралы видаЭти интегралы вычисляются методом разложения на основании тригонометрических тождеств.
- 44. Слайд 44
- 45. Слайд 45
- 46. Можно устно внести под знак дифференциала:Тогда
- 47. Рассмотрим три способа.
- 48. Проверка.
- 49. Слайд 49
- 50. Слайд 50
- 51. Слайд 51
- 52. Учебный вопрос 8.3. Определенный интеграл
- 53. Рассмотрим фигуру, ограниченную слева и справа прямыми
- 54. Слайд 54
- 55. Слайд 55
- 56. Слайд 56
- 57. Слайд 57
- 58. Слайд 58
- 59. Слайд 59
- 60. Слайд 60
- 61. Слайд 61
- 62. Слайд 62
- 63. Слайд 63
- 64. Слайд 64
- 65. Слайд 65
- 66. Слайд 66
- 67. Слайд 67
- 68. Слайд 68
- 69. Слайд 69
- 70. Слайд 70
- 71. Раздел 6. Дифференциальное исчисление функции одной переменной. Орлик Л.К.
- 72. Скачать презентанцию
Раздел 8.Интегральное исчисление функций одной переменной. Орлик Л.К.
Слайды и текст этой презентации
Слайд 1Управление
социальными системами
8. Интегральное исчисление функций одной переменной
Орлик
Любовь
Константиновна
Слайд 4Ранее мы по данной функции вычисляли ее производную. Сегодня мы
поставим обратную задачу: для данной функции
найти такую функцию производная которой равнялась бы заданной функции т.е.Слайд 6Таким образом,
- это совокупность всех первообразных от данной функции.
Определение
2. Пусть - одна из первообразных для функции Тогда выражение где - произвольная постоянная, называется неопределенным интегралом и обозначается
Слайд 27Теорема. Любая непрерывная на отрезке функция имеет на этом отрезке
первообразную.
Действие отыскания неопределенного интеграла или, что то же самое, нахождение
всех первообразных от данной функции, называется интегрированием этой функции.Дифференцирование и интегрирование являются взаимно обратными операциями.
Слайд 28Назовем график первообразной функции от интегральной
кривой.
Геометрический смысл неопределенного интеграла
Таким образом, если
то график функции
есть интегральная кривая.Слайд 31В дифференциальном исчислении производная от любой элементарной функции есть функция
элементарная. Другое дело операция, обратная дифференцированию, – интегрирование.
Интегралы, не берущиеся
в элементарных функцияхСлайд 32Можно привести примеры элементарных функций, первообразные от которых хотя и
существуют, но не являются элементарными функциями. Так, например, по теореме
существования дляфункций
существуют первообразные, но они не выражаются в элементарных функциях.
Слайд 33Несмотря на это, все эти первообразные хорошо изучены и для
них составлены таблицы, помогающие практически использовать эти функции.
Так, например, большое
значение в приложениях играет первообразная
от функции
удовлетворяющая дополнительному условию
Слайд 34Эта функция встречается в теории вероятностей и называется интегралом вероятностей.
Если
первообразная для некоторой функции не является элементарной функцией, то говорят,
что интеграл не берется в элементарных функциях.Слайд 434) Интегралы вида
Эти интегралы вычисляются методом разложения на основании
тригонометрических тождеств.
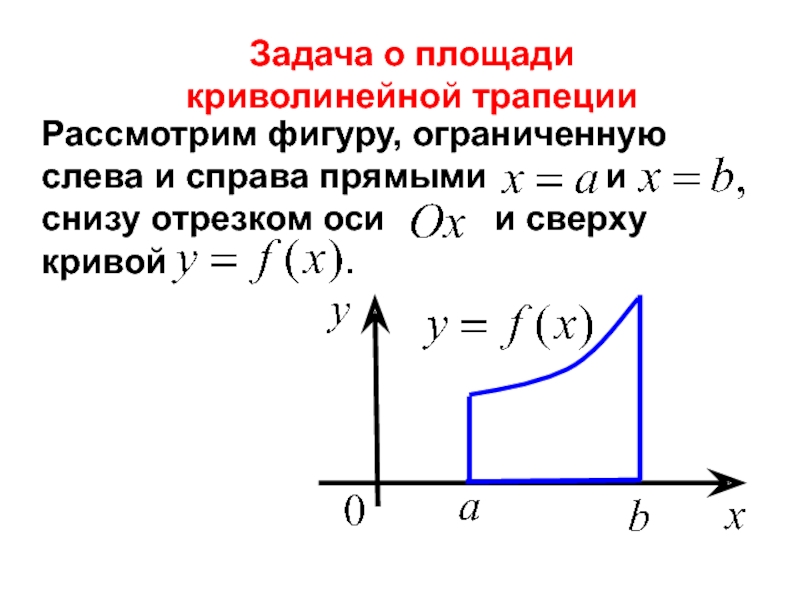
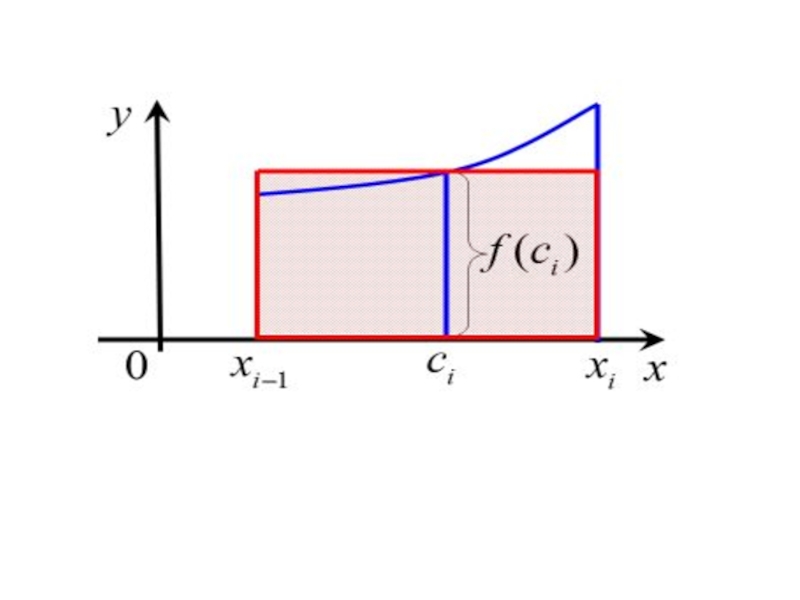
Слайд 53Рассмотрим фигуру, ограниченную слева и справа прямыми
и снизу отрезком
оси и сверху кривойЗадача о площади
криволинейной трапеции