Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок 1
Содержание
- 1. Урок 1
- 2. Цель урока. Дать понятие дифференциала функции как
- 3. ЛАГРАНЖ (Lagrange) Жозеф Луи (25 января 1736,
- 4. В 1754 в возрасте 18 лет стал
- 5. Автор трудов по вариационному исчислению. Им разработаны
- 6. КОШИ (Cauchy) Огюстен Луи (1789-1857), французский математик,
- 7. 1. Сравнение бесконечно малых величин. Известно, что
- 8. Малую по отношению к
- 9. 2. Понятие дифференциала функции.Рассмотрим функцию Найдем ее
- 10. Из таблицы видно, что первое слагаемое уменьшается
- 11. Значит, И здесь первое слагаемое с уменьшением
- 12. Дифференциал функции равен произведению производной функции на
- 13. Слайд 13
- 14. Примеры.Найти дифференциал функции 2.Найти дифференциал функции
- 15. 3. Найти дифференциал функции 4. Найти приближенное значение приращения функции
- 16. Точное значение приращения 5. Найти приближенное значение функции Найдем точное значение функции:
- 17. Подведение итогов урока.Домашнее задание. [2] с245-253 №478,481,511,512-516.
- 18. Скачать презентанцию
Цель урока. Дать понятие дифференциала функции как главной части приращения функции. Показать приложения дифференциала к приближенным вычислениям.Прививать интерес к предмету, используя исторический материал. Отметить, что современная интерпретация дифференциала как главной части
Слайды и текст этой презентации
Слайд 2Цель урока. Дать понятие дифференциала функции как главной части приращения
функции. Показать приложения дифференциала к приближенным вычислениям.
используя исторический материал. Отметить, что современная интерпретация дифференциала как главной части приращения функции дана Ж.Лагранжем, а окончательно была сформулирована О.Коши.Слайд 3ЛАГРАНЖ (Lagrange) Жозеф Луи (25 января 1736, Турин — 10
апреля 1813, Париж), французский математик и механик, иностранный почетный член
Петербургской АН (1776).Слайд 4В 1754 в возрасте 18 лет стал профессором артиллерийской школы
Турина. Организовал кружок, из которого впоследствии выросла Туринская академия наук.
Академия издавала публикации Лагранжа — в том числе по математическим проблемам азартных игр, движения жидкостей, сотрясения струн. В 1766 стал президентом Берлинской академии наук, в 1787 — действительным членом Парижской академии наук. Учавствовал в разработке метрической системы мер в парижском Институте и Бюро долгот. Во время Великой французской революции (1789) получил должность сенатора.Ж. Л. Лагранж
Слайд 5Автор трудов по вариационному исчислению. Им разработаны основные понятия и
методы по математическому анализу, теории чисел, алгебре, дифференциальным уравнениям. В
трактате «Аналитическая механика» (1788) в основу статики положил принцип возможных перемещений, в основу динамики — сочетание этого принципа с принципом Д'Аламбера (принцип Д'Аламбера — Лагранжа), придал уравнениям движения формулу, названную его именем. Уравнение Лагранжа используется в гидродинамике и общей механике. Его сочинения по математике, астрономии и механике составляют 14 томов.Ж. Л. Лагранж
Слайд 6КОШИ (Cauchy) Огюстен Луи (1789-1857), французский математик, иностранный почетный член
Петербургской АН (1831). Один из основоположников теории аналитических функций. Труды
по теории дифференциальных уравнений, математической физике, теории чисел, геометрии. Автор классических курсов математического анализа.Коши Огюстен Луи
Слайд 71. Сравнение бесконечно малых величин.
Известно, что при сложении, вычитании
и умножении бесконечно малых величин получаются величины бесконечно малые. Рассмотрим
деление.Слайд 8Малую по отношению к называют бесконечно
малой высшего порядка, а по отношению к
- бесконечно малой низшего порядка. имеют одинаковый порядок малости.Слайд 92. Понятие дифференциала функции.
Рассмотрим функцию
Найдем ее приращение.
Сравним изменение величин
обоих слагаемых последнего равенства с уменьшением .
Положив, например, и, следовательно, составим следующую таблицу значенийСлайд 10Из таблицы видно, что первое слагаемое уменьшается пропорционально
, а второе значительно быстрее.
Покажем, что то же самое
справедливо для любой дифференцируемой функции Мы знаем, что постоянная величина называется пределом переменной , если разность между ними есть величина бесконечно малая
Слайд 11Значит,
И здесь первое слагаемое с уменьшением уменьшается пропорционально
а второе значительно быстрее, им можно пренебречь.
Выражение называют главной частью приращения функцииГлавная часть приращения функции называется дифференциалом функции.












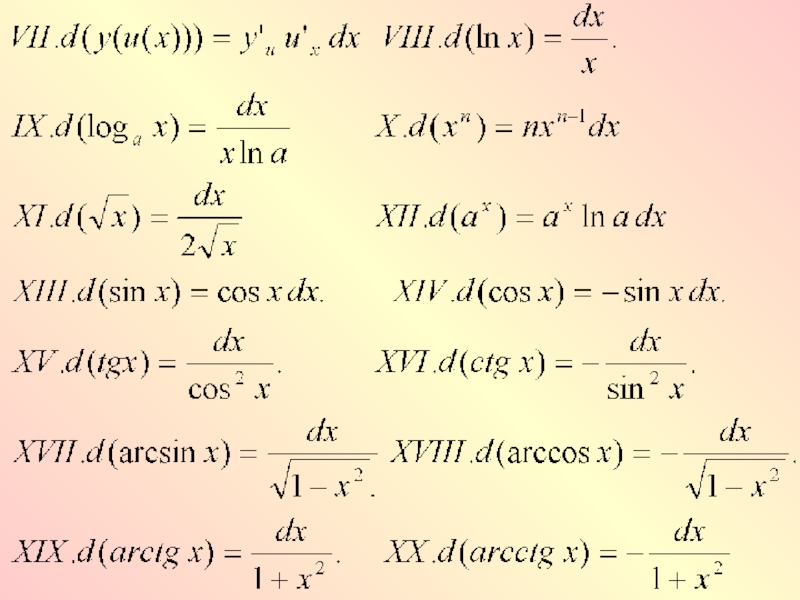



![Урок 1 Подведение итогов урока.Домашнее задание. [2] с245-253 №478,481,511,512-516. Подведение итогов урока.Домашнее задание. [2] с245-253 №478,481,511,512-516.](/img/tmb/6/597544/cafd262078950bece9945d8a8061666b-800x.jpg)



















