Слайд 1Векторная алгебра
Основные понятия
Слайд 2Учебники
1. А.В. Клетеник. Сборник задач по аналитической геометрии.
2. Г.Н. Берман.
Сборник задач по курсу математического анализа.
3. М.Л. Каган, М.В. Самохин.
Математика в инженерном вузе. Алгебра и геометрия.
4. Н.С. Пискунов. Дифференциальное и интегральное исчисление для втузов. Том I.
Слайд 3Основные понятия
Математическая величина
Скалярная величина
(характеризуется численным
значением)
Векторная величина
(Характеризуется численным
значением и
направлением)
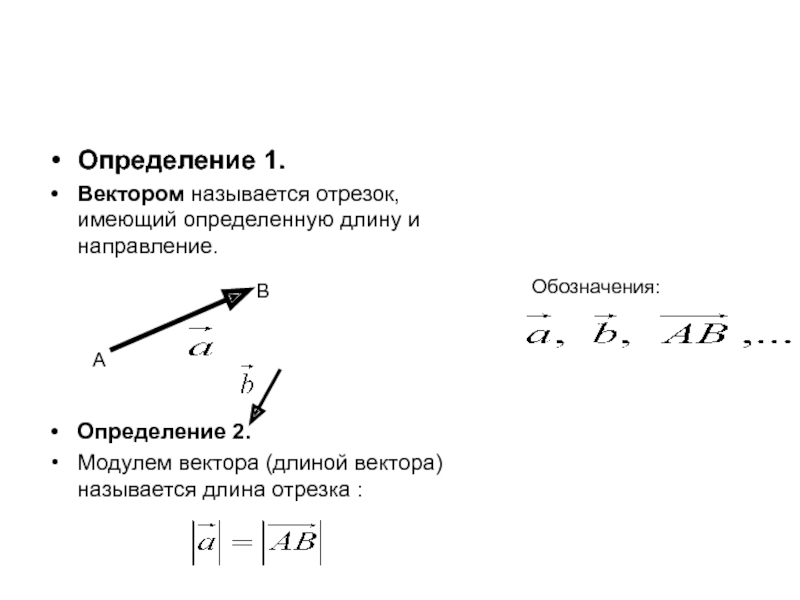
Слайд 4Определение 1.
Вектором называется отрезок, имеющий определенную длину и направление.
Определение
2.
Модулем вектора (длиной вектора) называется длина отрезка :
А
В
Обозначения:
Слайд 5Основные понятия
- вектор, у которого начало и
конец совпадают.
Определение 3.
Коллинеарными называются векторы, если они лежат на одной
прямой или на параллельных прямых.
Определение 4.
Углом между векторами
называется наименьший угол,
на который надо повернуть
один из векторов, чтобы их
направления совпали.
Обозначение:
Слайд 6 Сонаправлеными называются коллинеарные векторы, имеющие одинаковое направление.
Обозначение:
Противоположно направлеными
называются коллинеарные векторы, имеющие противоположные направления.
Обозначение:
Слайд 7понятия
Определение 5.
Два вектора называются равными, если
они коллинеарные, имеют одинаковую
длину
и одинаковое направление.
Следствие.
При параллельном переносе получаются равные векторы.
Слайд 8Основные понятия
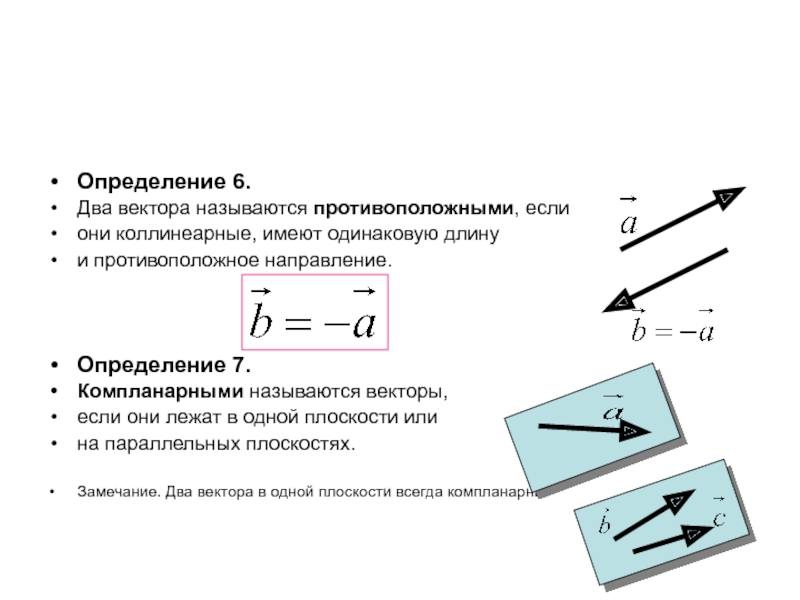
Определение 6.
Два вектора называются противоположными, если
они коллинеарные, имеют одинаковую
длину
и противоположное направление.
Определение 7.
Компланарными называются векторы,
если они лежат в одной
плоскости или
на параллельных плоскостях.
Замечание. Два вектора в одной плоскости всегда компланарны.
Слайд 9Операции с векторами
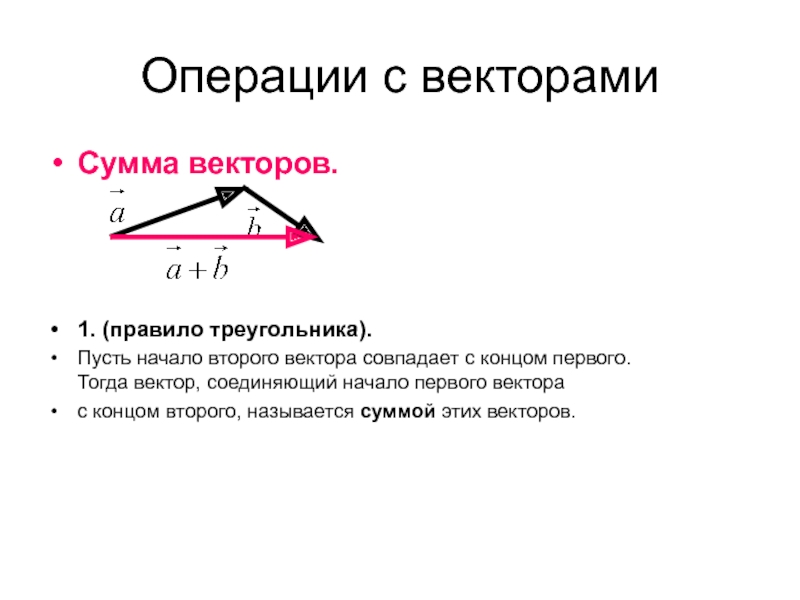
Сумма векторов.
1. (правило треугольника).
Пусть начало второго вектора совпадает
с концом первого. Тогда вектор, соединяющий
начало первого вектора
с концом второго, называется суммой этих векторов.
Слайд 10Операции с векторами
Сумма векторов.
2. (правило параллелограмма).
Пусть начала первого и второго
векторов совпадают.
Построим на этих векторах параллелограмм.
Тогда вектор,
совпадающий с диагональю, проходящей
через общее начало, называется суммой этих векторов.
Слайд 11Операции с векторами
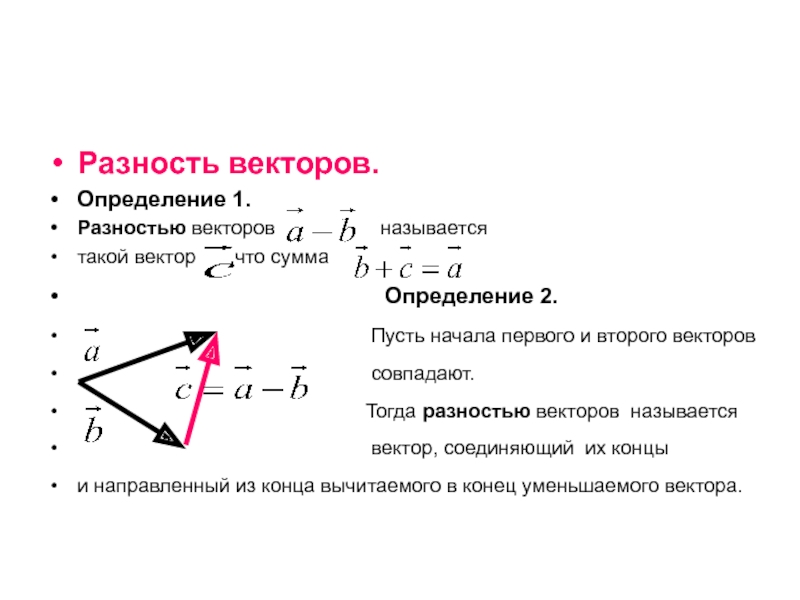
Разность векторов.
Определение 1.
Разностью векторов
называется
такой вектор
,что сумма
Определение 2.
Пусть начала первого и второго векторов
совпадают.
Тогда разностью векторов называется
вектор, соединяющий их концы
и направленный из конца вычитаемого в конец уменьшаемого вектора.
Слайд 12Операции с векторами
Произведение вектора на число.
Определение.
Произведением вектора
на число называется
вектор
,
коллинеарный вектору ,
равный по модулю ,
направленный при в ту же сторону, что и ,
и в противоположную сторону, если .
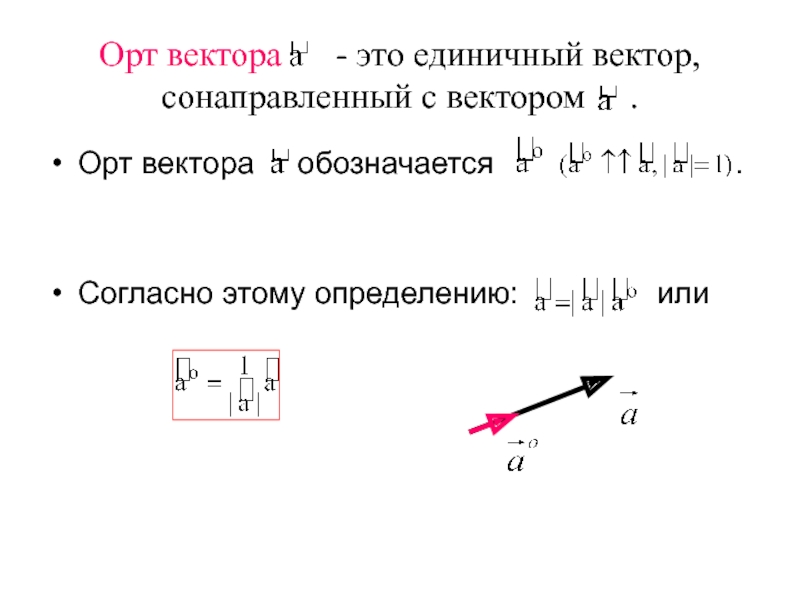
Слайд 13Орт вектора - это единичный вектор, сонаправленный с
вектором .
Орт вектора обозначается
.
Согласно этому определению: или
Слайд 14Операции с векторами
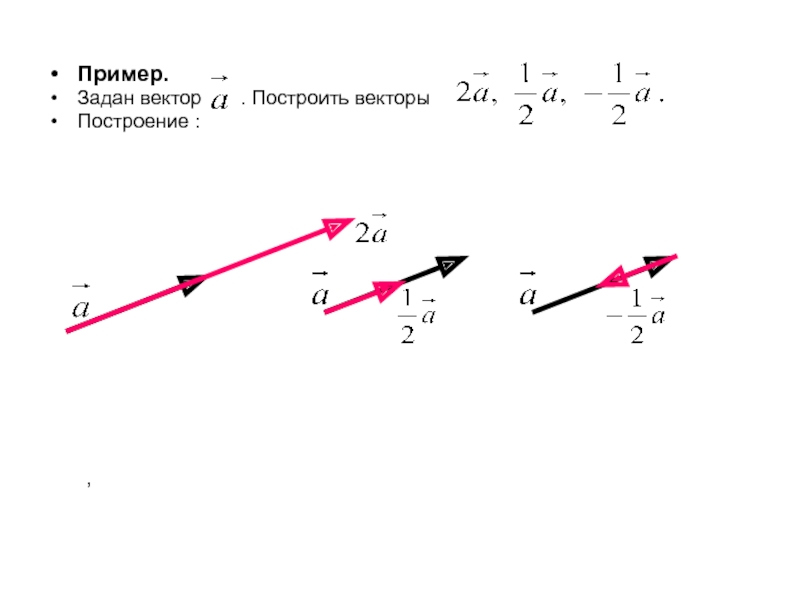
Пример.
Задан вектор . Построить векторы
Построение
:
,
Слайд 15Теорема. Необходимое и достаточное условие коллинеарности двух векторов
Для того, чтобы
два вектора и были коллинеарны, необходимо
и достаточно, чтобы один из них мог быть представлен в виде произведения некоторого числа на другой вектор, т.е.
(или ).
Слайд 16В этой теореме мы должны доказать два признака: один из
них является необходимым для данного утверждения, а другой – достаточным.
Что это значит?
Пусть имеется некоторое утверждение и какой-либо признак для проверки справедливости этого утверждения.
Если из справедливости данного утверждения следует выполнение признака, то такой признак называется необходимым для данного утверждения.
Слайд 17 Если же наоборот – из выполнения признака
следует справедливость утверждения, то такой признак называется достаточным для данного
утверждения.
Признак может быть только необходимым, или только достаточным, или одновременно и достаточным и необходимым.
Слайд 18Доказательство теоремы о необходимом и достаточном условии коллинеарности двух векторов
разобьем на две части.
Докажем необходимость.
Если один из векторов, например,
то
(при ) и теорема доказана.
Пусть векторы коллинеарны,
Докажем, что существует действительное число
такое, что .
Слайд 19Рассмотрим орты векторов :
а) Если
векторы сонаправлены, то
, т.е.
или .
Обозначив , получим . Заметим, что
Слайд 20б) Если векторы направлены противоположно,
то
т.е. или .
Обозначив , получим .
Заметим. что в этом случае
Таким образом, если векторы коллинеарны, то
Слайд 21Основные свойства операций над векторами
1.
2.
3.
4.
5.
6.
Самостоятельно доказать свойства 1,3-6.
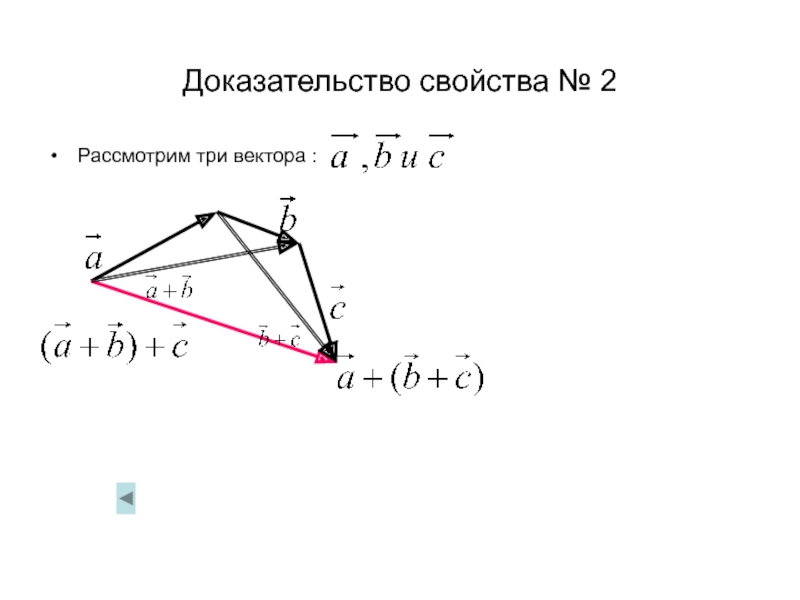
Слайд 22Доказательство свойства № 2
Рассмотрим три вектора :
Слайд 23Базисом на плоскости называются любые два неколлинеарных вектора в этой
плоскости.
Слайд 24Разложение векторов по базису на плоскости.
Теорема 1.
Пусть векторы
и - неколлинеарные,
векторы
- компланарные.
Тогда найдутся такие постоянные и ,
что
Такое разложение единственное.
Доказательство.
Слайд 25Единственность.
Предположим :
Пусть
(хотя бы одно из неравенств
и
выполнено)
Слайд 26Разложение векторов в пространстве
Теорема 2.
Пусть векторы
- некомпланарные.
Тогда найдутся такие
постоянные ,
что любой вектор можно записать
в виде
(разложить по векторам ).
Такое разложение единственное.
Д.з. Самостоятельно построить
чертеж и получить разложение
Слайд 27Разложение векторов в прямоугольной системе координат
Рассмотрим прямоугольную систему координат.
Теорема 3.
В
пространстве любой вектор можно разложить по ортонормированному
базису :
Такое разложение единственное.
Векторы -единичные (орты),
направленные по осям x, y, z (соответственно)
Определение 2.
Тройка векторов называется
ортонормированным базисом
в пространстве.
Слайд 28Координаты вектора
Определение 3.
Коэффициенты x, y, z разложения
называются прямоугольными координатами
вектора
:
Частный случай.
Если вектор
расположен на координатной плоскости хоу,
то разложение будет иметь вид
Коэффициенты х, у называются прямоугольными координатами
вектора на плоскости :
Слайд 29Проекции вектора
Рассмотрим вектор
и ось
Определение.
Проекцией вектора
на ось называется
разность проекций конца и начала вектора на эту ось;
0
Слайд 30Свойства проекций (Доказать самостоятельно).
1.
2.
3.
4. Связь координат вектора и проекций на
оси.
Пусть вектор на плоскости имеет
разложение:
х
у
0
Слайд 31Следовательно,
Координаты вектора – это его проекции на оси координат.
Слайд 32Координаты вектора в пространстве
Следствие.
Если вектор
задан двумя точками,
- начало, - конец,
то
Слайд 33Действия с векторами, заданными
в координатной форме
Сумма и разность векторов,
произведение вектора на число.
Пусть
Тогда
1.
2.
Модуль вектора
Орт вектора
Слайд 34Необходимое и достаточное условие коллинеарности
векторов, заданных в координатной форме.
Два ненулевых
вектора коллинеарны тогда и только тогда, когда
соответствующие координаты этих
векторов пропорциональны.
Пусть
Тогда
Доказательство.