Слайд 1Векторный анализ
§ 1. Скалярные и векторные поля.
Определение. (скалярного поля). Если
в трехмерном пространстве определена функция u(x,y,z), то говорят, что задано
скалярное поле u(x,y,z).
Замечание. Другими словами говоря, задание скалярного поля означает, что каждой точке M(x,y,z) поставлено в соответствие число, которое является значением функции u в точке M.
Слайд 2Пример. Скалярного поля. Если в начало координат поместить заряд Q,
то в каждой точке пространства определена функция
,
где: - расстояние от точки до начала координат; - потенциал,
0 – диэлектрическая постоянная вакуума.
Задание функции задает скалярное поле потенциала.
Слайд 3Определение. (векторного поля). Говорят, что в трехмерном пространстве задано векторное
поле
Замечание. В этом случае каждой точке пространства M(x,y,z) ставится в
соответствие вектор в точке M(x,y,z).
Для скалярных и векторных полей вводится понятие поверхностей уровня.
Определение. (поверхностей уровня). Пусть задано скалярное поле u(x,y,z). Поверхностью уровня данного скалярного поля, называется поверхность, задаваемая уравнением
u(x,y,z) = сonst.
Слайд 4Пример. Поверхности уровня. Если в начало координат поместить заряд Q,
то имеем скалярное поле потенциала
,
Поверхностью уровня является поверхность:
где: с = const.
- сфера
Такие поверхности называются эквипотенциальными.
Слайд 5Определение. (векторной линии). Пусть в трехмерном пространстве задано векторное поле
Векторной
линией заданного векторного поля называется линия, в каждой точке которой
вектор касательной совпадает по направлению с вектором .
Замечание. Уравнение векторных линий можно находить по формуле:
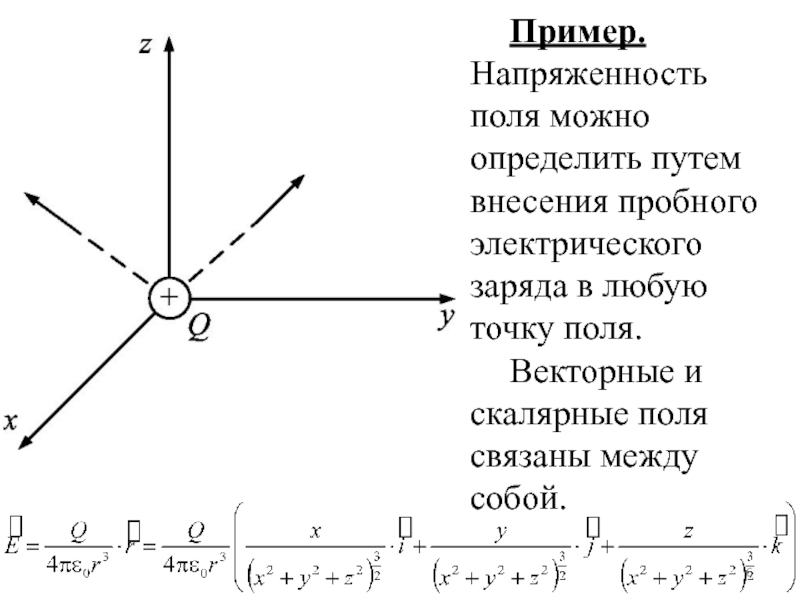
Слайд 6Пример. Напряженность поля можно определить путем внесения пробного электрического заряда
в любую точку поля.
Векторные и скалярные поля связаны между
собой.
Слайд 7§ 2. Производная по направлению.
Ее вычисление.
Пусть задано скалярное поле
u, где u – дифференцируемая функция. Возьмем в трехмерном пространстве
вектор l, расположенный в этом скалярном поле. Пусть
начало вектора l характеризует
точку М0. Возьмем на векторе l
соседнюю точку М . Точка М как
и М0 находится в скалярном поле u . Поэтому имеет смысл приращение скалярного поля u в точке М0, выраженное формулой:
Слайд 8Df. (производной по направлению): если существует конечный предел отношения приращения
скалярного поля
к длине вектора,
т.е. к , то этот предел называется производной скалярного поля u по направлению l и обозначается:
Слайд 9Чтобы вычислить производную по направлению, пользуются теоремой:
Th.: (о вычислении производной
по направлению).
Если скалярное поле u(x,y,z) дифференцируемо в каждой точке некоторой
области V, то производная по направлению в каждой точке V существует и она выражается формулой:
Слайд 10где a,b,g - углы определенные в любой точке области V
, которые составляет вектор l с координатными осями.
Док-во: т.к. скалярное
поле u дифференцируется в области V, значит, в любой окрестности точки М0 V существует приращение скалярного поля, находимого по формуле:
Слайд 11здесь a1,a2,a3 - бесконечно малые функции в точке М0 ,
которые стремятся к 0, когда
- это проекции вектора ,
совпадающего по направлению с вектором на
координатные оси.
- частные производные.
Разделим левую и правую части на длину вектора
После чего получаем:
Слайд 12Перейдем к пределу в выражении (2) при
Заметим, что
Если заменить x
на y и x на z, то в пределе получим
cos и cos.
Слайд 13Значит, в пределе, учитывая, что
1, 2, 3 0 при
,
имеем:
Так как предел правой части (2) существует и выражается правой частью формулы (3), то и предел левой части формулы (3) существует. Он равен производной скалярного поля по направлению. Значит, производная скалярного поля u по направлению l выражается формулой:
Слайд 14Что и требовалось доказать.
Замечание: Производная скалярного поля по направлению вектора
выражает скорость возрастания или убывания скалярного поля по направлению
вектора , если:
- поле возрастает
- поле убывает.
Вычисление скалярного поля производится по формуле (4).
Пример: на практике.
Слайд 15§ 3. Градиент скалярного поля. Связь скалярных и векторных полей.
Свойства градиента
Определение. (градиента). Градиентом дифференцируемого скалярного поля называется вектор
.
Замечание. На практике встречаются равносильные обозначения градиента:
gradu u,
где: - оператор «Набла».
Слайд 16Определение градиента привязано к декартовой системе координат. Покажем связь скалярных
и векторных полей.
Пусть задано скалярное поле u(x,y,z), дифференцируемое в некотором
V.
-произвольный вектор V. По определению:
Но эта запись означает, что скалярному полю u c помощью grad поставлено в соответствие векторное поле grad. Что и говорит о том, что скалярное и векторное поле связаны между собой.
Слайд 17Вспомним, что скалярное произведение 2-х векторов вычисляется по формуле:
Найдем скалярное
произведение градиента поля u и вектора , получим:
- произвольный единичный вектор V.
В правой части производная по направлению:
Слайд 18По этой формуле можно вычислять производную по направлению, зная градиент.
Учитывая,
что:
= проекцияlgradu =
Df. (инвариантное определение градиента, не зависящего от системы координат).
Градиентом скалярного поля u называется вектор, обозначенный gradu, проекция которого
Слайд 19на произвольное направление вектора равна производной скалярного
поля по направлению этого вектора .
Свойства градиента:
Градиент дифференцируемого
скалярного поля u(x,y,z) перпендикулярен к поверхности уровня этого скалярного поля (совпадает с нормалью) и направлен в сторону возрастания скалярного поля.
2. grad(c1u1 + c2u2) = c1gradu1 + c2gradu2,
c1, c2 = const;
u1, u2 – скалярные поля.
3. grad(u1u2) = u2gradu1 + u1gradu2.
Слайд 20
4.
5. Если задано скалярное поле F(u(x,y,z)), то градиент:
gradF(u(x,y,z)) =
Fugradu.
§ 4. Применение градиента для вычисления нормали к поверхности.
Для поля
u(x,y,z) введем понятие градиента:
Слайд 21Если имеется уравнение поверхности
u(x,y,z) = 0, это означает, что задана
поверхность уровня скалярного поля u(x,y,z).
Так как градиент скалярного поля направлен
по нормали к поверхности уровня, то единичный вектор нормали к поверхности можно найти по формуле:
Пример. На практике