Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вероятность и статистика на ЕГЭ 2014 г
Содержание
- 1. Вероятность и статистика на ЕГЭ 2014 г
- 2. В случайном эксперименте бросают две игральные кости.
- 3. В случайном эксперименте бросают три игральные кости.
- 4. Игральный кубик бросают дважды. Сколько элементарных исходов
- 5. В чемпионате по гимнастике участвуют 40 спортсменок:
- 6. В среднем из 500 садовых насосов, поступивших
- 7. Фабрика выпускает сумки. В среднем на 80
- 8. Научная конференция проводится в 3 дня. Всего
- 9. Перед началом первого тура чемпионата по шашкам
- 10. В сборнике билетов по химии всего 25
- 11. В случайном эксперименте симметричную монету бросают пять
- 12. Две фабрики выпускают одинаковые стекла для автомобильных
- 13. Марина, Катя, Вова, Лена, Миша, Артур, Ваня
- 14. На экзамене по геометрии школьнику достаётся один
- 15. В торговом центре два одинаковых автомата продают
- 16. Решение. Рассмотрим события А = кофе закончится
- 17. Биатлонист 4 раза стреляет по мишеням. Вероятность
- 18. Решение. Поскольку биатлонист попадает в мишени с
- 19. В магазине стоят два платёжных автомата. Каждый
- 20. Решение. Найдем вероятность того, что неисправны оба
- 21. Помещение освещается фонарём с двумя лампами. Вероятность
- 22. Вероятность того, что новый тостер прослужит больше
- 23. Агрофирма закупает куриные яйца в двух домашних
- 24. На клавиатуре телефона 10 цифр, от 0
- 25. Из множества натуральных чисел от 51 до
- 26. Ковбой Джон попадает в муху на стене
- 27. В группе туристов 8 человек. С помощью
- 28. Перед началом футбольного матча судья бросает монетку,
- 29. На рок-фестивале выступают группы — по одной от
- 30. Чтобы пройти в следующий круг соревнований, футбольной
- 31. Решение. Команда может получить не меньше 7
- 32. В некотором городе из 3000 появившихся на
- 33. На борту самолёта 18 мест рядом с
- 34. На олимпиаде по биологии участников рассаживают по
- 35. В классе 33 учащихся, среди них два
- 36. В группе туристов 16 человек. Их вертолётом
- 37. Вероятность того, что новый блендер в течение
- 38. При изготовлении подшипников диаметром 68 мм вероятность
- 39. Вероятность того, что на тесте по истории
- 40. Чтобы поступить в институт на специальность «Переводчик»,
- 41. Решение. Для того, чтобы поступить хоть куда-нибудь,
- 42. По отзывам покупателей Василий Васильевич оценил надёжность
- 43. Из районного центра в деревню ежедневно ходит
- 44. Перед началом волейбольного матча капитаны команд тянут
- 45. В Волшебной стране бывает два типа погоды:
- 46. Решение. Для погоды на 4, 5 и
- 47. Механические часы с двенадцатичасовым циферблатом в какой-то
- 48. В кармане у Димы было четыре конфеты —
- 49. Вероятность того, что батарейка бракованная, равна 0,02.
- 50. Автоматическая линия изготавливает батарейки. Вероятность того, что
- 51. На рисунке изображён лабиринт. Паук заползает в
- 52. Самостоятельная работа. Дома:
- 53. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2В случайном эксперименте бросают две игральные кости. Найдите вероятность того,
что в сумме выпадет 5 очков. Результат округлите до сотых.
n
= 36m =
p =
(1; 4)
(2; 3)
(3; 2)
(4; 1)
4
0,1111
Ответ: 0,11
Слайд 3В случайном эксперименте бросают три игральные кости. Найдите вероятность того,
что в сумме выпадет 15 очков. Результат округлите до сотых.
n
= 216m =
p =
(3; 6; 6)
(4; 5; 6)
(4; 5; 6)
(5; 4; 6)
(5; 6; 4)
(6; 6; 3)
(6; 3; 6)
7
0,0324
Ответ: 0,03
Слайд 4Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию
А = {сумма очков равна 4}?
n = 36
m =
p
= (1; 3)
(2; 2)
(3; 1)
3
0,0833
Ответ: 0,08
Слайд 5В чемпионате по гимнастике участвуют 40 спортсменок: 12 из Аргентины,
9 из Бразилии, остальные — из Парагвая. Порядок, в котором выступают
гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Парагвая.Ответ: 0,475
Слайд 6В среднем из 500 садовых насосов, поступивших в продажу, 4
подтекают. Найдите вероятность того, что один случайно выбранный для контроля
насос не подтекает.Слайд 7Фабрика выпускает сумки. В среднем на 80 качественных сумок приходится
одна сумка со скрытыми дефектами. Найдите вероятность того, что купленная
сумка окажется качественной. Результат округлите до сотых.Ответ: 0,99
Слайд 8Научная конференция проводится в 3 дня. Всего запланировано 70 докладов — в
первый день 28 докладов, остальные распределены поровну между вторым и третьим
днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?Слайд 9Перед началом первого тура чемпионата по шашкам участников разбивают на
игровые пары случайным образом с помощью жребия. Всего в чемпионате
участвует 36 шашистов, среди которых 15 участников из России, в том числе Евгений Коротов. Найдите вероятность того, что в первом туре Евгений Коротов будет играть с каким-либо шашистом из России?В первом туре Евгений Коротов может сыграть с 36 − 1 = 35 бадминтонистами, из которых 15 − 1 = 14 из России. Значит, вероятность того, что в первом туре Евгений Коротов будет играть с каким-либо бадминтонистом из России, равна
Слайд 10В сборнике билетов по химии всего 25 билетов, в 6
из них встречается вопрос по углеводородам. Найдите вероятность того, что
в случайно выбранном на экзамене билете школьнику достанется вопрос по углеводородам.Слайд 11В случайном эксперименте симметричную монету бросают пять раз. Найдите вероятность
того, что орел выпадет ровно 4 раза.
n = 32
m =
p =
(о; о; о; о; р)
(о; о; о; р; о)
(о; о; р; о; о)
(о; р; о; о; о)
(р; о; о; о; о)
5
0,15625
Слайд 12Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика
выпускает 70 этих стекол, вторая — 30. Первая фабрика выпускает 5
бракованных стекол, а вторая — 4. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.Слайд 13Марина, Катя, Вова, Лена, Миша, Артур, Ваня и Сеня бросили
жребий — кому начинать игру. Найдите вероятность того, что начинать игру
должен будет Ваня.Слайд 14На экзамене по геометрии школьнику достаётся один вопрос из списка
экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная
окружность», равна 0,1. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,35. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.Слайд 15В торговом центре два одинаковых автомата продают кофе. Вероятность того,
что к концу дня в автомате закончится кофе, равна 0,2.
Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.Слайд 16Решение. Рассмотрим события
А = кофе закончится в первом автомате,
В = кофе закончится во втором автомате.
Тогда A·B =
кофе закончится в обоих автоматах, A + B = кофе закончится хотя бы в одном автомате.
По условию P(A) = P(B) = 0,2; P(A·B) = 0,16.
События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:
P(A + B) = P(A) + P(B) − P(A·B) = 0,2 + 0,2 − 0,16 = 0,24.
Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,24 = 0,76.
Ответ: 0,76.
Слайд 17Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень
при одном выстреле равна 0,7. Найдите вероятность того, что биатлонист
первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.Слайд 18
Решение. Поскольку биатлонист попадает в мишени с вероятностью 0,7, он
промахивается с вероятностью 1 − 0,7 = 0,3. Cобытия попасть или промахнуться при каждом
выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей. Тем самым, вероятность события «попал, попал, промахнулся, промахнулся» равна 0,70,70,30,3 = 0,0441Ответ: 0,0441.
Слайд 19В магазине стоят два платёжных автомата. Каждый из них может
быть неисправен с вероятностью 0,09 независимо от другого автомата. Найдите
вероятность того, что хотя бы один автомат исправен.Слайд 20Решение. Найдем вероятность того, что неисправны оба автомата. Эти события
независимые, вероятность их произведения равна произведению вероятностей этих событий: 0,09 · 0,09 = 0,0081.
Событие, состоящее в том, что исправен хотя бы один автомат, противоположное. Следовательно, его вероятность равна 1 − 0,0081 = 0,9919.
Ответ: 0,9919.
Слайд 21Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы
в течение года равна 0,22. Найдите вероятность того, что в
течение года хотя бы одна лампа не перегорит.Найдем вероятность того, что перегорят обе лампы. Эти события независимые, вероятность их произведения равно произведению вероятностей этих событий: 0,22·0,22 = 0,0484.
Событие, состоящее в том, что не перегорит хотя бы одна лампа, противоположное. Следовательно, его вероятность равна 1 − 0,0484 = 0,9516.
Ответ: 0,9416.
Слайд 22Вероятность того, что новый тостер прослужит больше года, равна 0,94.
Вероятность того, что он прослужит больше двух лет, равна 0,8.
Найдите вероятность того, что он прослужит меньше двух лет, но больше года.P(A + B) = P(A) + P(B) − P(A·B) = P(A) + P(B),
откуда, используя данные из условия, получаем
0,94 = P(A) + 0,8.
Тем самым, для искомой вероятности имеем:
P(A) = 0,94 − 0,8 = 0,14.
Ответ: 0,14.
Слайд 23Агрофирма закупает куриные яйца в двух домашних хозяйствах. 60% яиц
из первого хозяйства — яйца высшей категории, а из второго хозяйства —
70% яиц высшей категории. Всего высшую категорию получает 65% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.Пусть берут 100 яиц высшей категории.
Слайд 24На клавиатуре телефона 10 цифр, от 0 до 9. Какова
вероятность того, что случайно нажатая цифра будет нечётной?
Слайд 25Из множества натуральных чисел от 51 до 78 наудачу выбирают
одно число. Какова вероятность того, что оно делится на 2?
Слайд 26Ковбой Джон попадает в муху на стене с вероятностью 0,7,
если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного
револьвера, то он попадает в муху с вероятностью 0,1. На столе лежит 10 револьверов, из них только 2 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.Р= 1 – (0,70,2 +0,10,8) =0,78
Слайд 27В группе туристов 8 человек. С помощью жребия они выбирают
двух человек, которые должны идти в село за продуктами. Турист
Б. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что Б. пойдёт в магазин?Слайд 28Перед началом футбольного матча судья бросает монетку, чтобы определить, какая
из команд начнёт игру с мячом. Команда «Геолог» играет три
матча с разными командами. Найдите вероятность того, что в этих играх «Геолог» выиграет жребий ровно один раз.Решение. Обозначим «1» ту сторону монеты, которая отвечает за выигрыш жребия «Геолог», другую сторону монеты обозначим «0». Тогда благоприятных комбинаций три: 110, 101, 011, а всего комбинаций 23 = 8: 000, 001, 010, 011, 100, 101, 110, 111. Тем самым, искомая вероятность равна:
Ответ: 0,375.
Слайд 29На рок-фестивале выступают группы — по одной от каждой из заявленных
стран. Порядок выступления определяется жребием. Какова вероятность того, что группа
из Франции будет выступать после группы из Швеции и после группы из России? Результат округлите до сотых.Решение. Общее количество выступающих на фестивале групп для ответа на вопрос неважно. Сколько бы их ни было, для указанных стран есть 6 способов взаимного расположения среди выступающих (Ф — Франции, Ш — Швеция, Р — России):
...Ф...Ш...Р..., ...Ф...Р...Ш..., ...Ш...Р...Ф..., ...Ш...Ф...Р..., ...Р...Ф...Ш..., ...Р..Ш...Ф...
Франции находится после Швеции и России в двух случаях. Поэтому вероятность того, что группы случайным образом будут распределены именно так, равна
Ответ: 0,33.
Слайд 30Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать
хотя бы 7 очков в двух играх. Если команда выигрывает,
она получает 6 очков, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,2.Слайд 31Решение. Команда может получить не меньше 7 очков в двух
играх тремя способами: 6+1, 1+6, 6+6. Эти события несовместны, вероятность
их суммы равна сумме их вероятностей. Каждое из этих событий представляет собой произведение двух независимых событий — результата в первой и во второй игре. Отсюда имеем:Ответ: 0,...
Слайд 32В некотором городе из 3000 появившихся на свет младенцев 1430
девочек. Найдите частоту рождения мальчиков в этом городе. Результат округлите
до тысячных.Слайд 33На борту самолёта 18 мест рядом с запасными выходами и
28 мест за перегородками, разделяющими салоны. Остальные места неудобны для
пассажира высокого роста. Пассажир Д. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру Д. достанется удобное место, если всего в самолёте 200 мест.Решение. В самолете 18 + 28 = 46 мест удобны пассажиру Д., а всего в самолете 200 мест. Поэтому вероятность того, что пассажиру Д. достанется удобное место равна 46 : 200 = 0,23.
Ответ: 0,23.
Слайд 34На олимпиаде по биологии участников рассаживают по трём аудиториям. В
первых двух по 150 человек, оставшихся проводят в запасную аудиторию
в другом корпусе. При подсчёте выяснилось, что всего было 400 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.Решение. Всего в запасную аудиторию направили 400 − 150 − 150 = 100 человек. Поэтому вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории, равна 100 : 400 = 0,25.
Ответ: 0,25.
Слайд 35В классе 33 учащихся, среди них два друга — Андрей и
Михаил. Класс случайным образом разбивают на 3 равные группы. Найдите
вероятность того, что Андрей и Михаил окажутся в одной группе.Решение. Пусть один из друзей находится в некоторой группе. Вместе с ним в группе окажутся 16 человек из 32 оставшихся одноклассников. Вероятность того, что друг окажется среди этих 16 человек, равна 16 : 32 = 0,5.
Слайд 36В группе туристов 16 человек. Их вертолётом в несколько приёмов
забрасывают в труднодоступный район по 4 человека за рейс. Порядок,
в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист У. полетит третьим рейсом вертолёта.Решение. На первом рейсе 4 мест, всего мест 16. Тогда вероятность того, что турист У. полетит третьим рейсом вертолёта, равна:
Слайд 37Вероятность того, что новый блендер в течение года поступит в
гарантийный ремонт, равна 0,096. В некотором городе из 1000 проданных
блендеров в течение года в гарантийную мастерскую поступило 102 штуки. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?Решение. Частота (относительная частота) события «гарантийный ремонт» равна 102 : 1000 = 0,102. Она отличается от предсказанной вероятности на 0,006.
Ответ: 0,006.
Слайд 38При изготовлении подшипников диаметром 68 мм вероятность того, что диаметр
будет отличаться от заданного не больше, чем на 0,01 мм,
равна 0,968. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 67,99 мм, или больше, чем 68,01 мм.1 − 0,968 = 0,032. Ответ: 0,032.
Слайд 39Вероятность того, что на тесте по истории учащийся Д. верно
решит больше 6 задач, равна 0,73. Вероятность того, что Д.
верно решит больше 5 задач, равна 0,84. Найдите вероятность того, что Д. верно решит ровно 6 задач.Решение. Рассмотрим события A = «учащийся решит 6 задач» и В = «учащийся решит больше 6 задач». Их сумма — событие A + B = «учащийся решит больше 5 задач». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B). Тогда, используя данные задачи, получаем: 0,84 = P(A) + 0,73, откуда P(A) = 0,84 − 0,73 = 0,11.
Слайд 40Чтобы поступить в институт на специальность «Переводчик», абитуриент должен набрать
на ЕГЭ не менее 79 баллов по каждому из трёх
предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Таможенное дело», нужно набрать не менее 79 баллов по каждому из трёх предметов — математика, русский язык и обществознание. Вероятность того, что абитуриент Б. получит не менее 79 баллов по математике, равна 0,9, по русскому языку — 0,7, по иностранному языку — 0,8 и по обществознанию — 0,9. Найдите вероятность того, что Б. сможет поступить на одну из двух упомянутых специальностей.Слайд 41Решение. Для того, чтобы поступить хоть куда-нибудь, Б. нужно сдать
и русский, и математику как минимум на 79 баллов, а
помимо этого еще сдать иностранный язык или обществознание не менее, чем на 79 баллов. Пусть A, B, C и D — это события, в которых Б. сдает соответственно математику, русский, иностранный и обществознание не менее, чем на 79 баллов. Тогда поскольку для вероятности поступления имеем:Доделай !
Слайд 42По отзывам покупателей Василий Васильевич оценил надёжность двух интернет-магазинов. Вероятность
того, что нужный товар доставят из магазина А, равна 0,8.
Вероятность того, что этот товар доставят из магазина Б, равна 0,88. Василий Васильевич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.Решение. Вероятность того, что первый магазин не доставит товар равна 1 − 0,8 = 0,2. Вероятность того, что второй магазин не доставит товар равна 1 − 0,88 = 0,12. Поскольку эти события независимы, вероятность их произведения (оба магазина не доставят товар) равна произведению вероятностей этих событий: 0,2 · 0,12 = 0,024. Ответ: 0,024.
Слайд 43Из районного центра в деревню ежедневно ходит автобус. Вероятность того,
что в понедельник в автобусе окажется меньше 20 пассажиров, равна
0,81. Вероятность того, что окажется меньше 12 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 12 до 19.Решение. Рассмотрим события A = «в автобусе меньше 20 пассажиров» и В = «в автобусе от 12 до 19 пассажиров». Их сумма — событие A + B = «в автобусе меньше 20 пассажиров». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B).
Тогда, используя данные задачи, получаем: 0,81 = 0,56 + P(В), откуда P(В) = 0,81 − 0,56 = 0,25.
Слайд 44Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы
определить, какая из команд начнёт игру с мячом. Команда «Стартер»
по очереди играет с командами «Протор», «Ротор» и «Мотор». Найдите вероятность того, что «Стартер» будет начинать только вторую и последнюю игры.Решение. Требуется найти вероятность произведения трех событий: «Статор» не начинает первую игру, начинает вторую игру, начинает третью игру. Вероятность произведения независимых событий равна произведению вероятностей этих событий. Вероятность каждого из них равна 0,5, откуда находим: 0,5·0,5·0,5 = 0,125.
Ответ: 0,125.
Слайд 45В Волшебной стране бывает два типа погоды: хорошая и отличная,
причём погода, установившись утром, держится неизменной весь день. Известно, что
с вероятностью 0,7 погода завтра будет такой же, как и сегодня. 6 сентября погода в Волшебной стране хорошая. Найдите вероятность того, что 9 сентября в Волшебной стране будет отличная погода.Слайд 46Решение. Для погоды на 4, 5 и 6 июля есть
4 варианта: ХХО, ХОО, ОХО, ООО (здесь Х — хорошая,
О — отличная погода). Найдем вероятности наступления такой погоды:P(XXO) = 0,7·0,7·0,3 = 0,147;
P(XOO) = 0,7·0,3·0,7 = 0,147;
P(OXO) = 0,3·0,3·0,3 = 0,027;
P(OOO) = 0,7·0,7·0,7 = 0,343.
Указанные события несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,147 + 0,147 + 0,027 + 0,343 = 0,664
Слайд 47Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и
перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув
отметки 5, но не дойдя до отметки 8 часов.Решение. На циферблате между пятью часами и восемью часами три часовых деления. Всего на циферблате 12 часовых делений. Поэтому искомая вероятность равна:
Слайд 48В кармане у Димы было четыре конфеты — «Коровка», «Красная шапочка»,
«Василёк» и «Ласточка», а так же ключи от квартиры. Вынимая
ключи, Дима случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Красная шапочка».Слайд 49Вероятность того, что батарейка бракованная, равна 0,02. Покупатель в магазине
выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность
того, что обе батарейки окажутся исправными.Решение. Вероятность того, что батарейка исправна, равна 0,98. Вероятность произведения независимых событий (обе батарейки окажутся исправными) равна произведению вероятностей этих событий: 0,98·0,98 = 0,9604.
Ответ: 0,9604.
Слайд 50Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна,
равна 0,03. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность
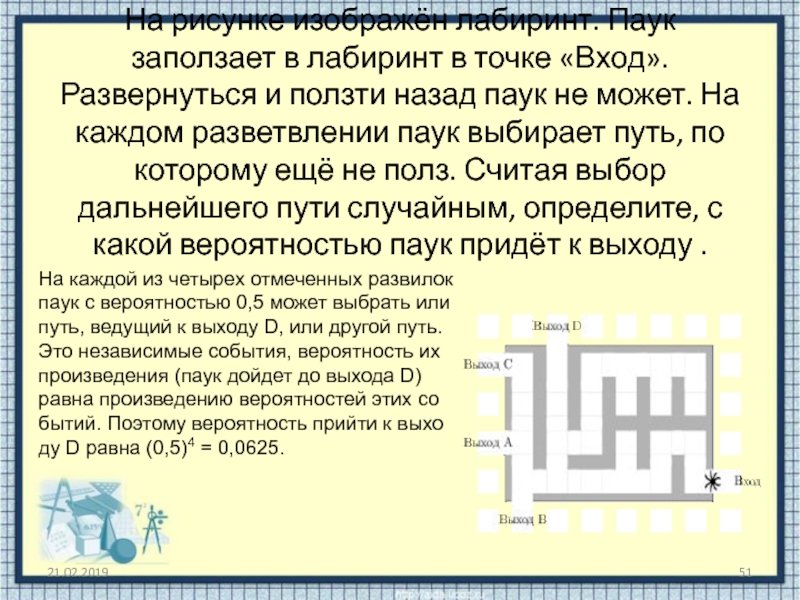
того, что система забракует неисправную батарейку, равна 0,95. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,04. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.Слайд 51На рисунке изображён лабиринт. Паук заползает в лабиринт в точке
«Вход». Развернуться и ползти назад паук не может. На каждом
разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу .На каждой из четырех отмеченных развилок паук с вероятностью 0,5 может выбрать или путь, ведущий к выходу D, или другой путь. Это независимые события, вероятность их произведения (паук дойдет до выхода D) равна произведению вероятностей этих событий. Поэтому вероятность прийти к выходу D равна (0,5)4 = 0,0625.