Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вероятность: концепция, терминология и измерение
Содержание
- 1. Вероятность: концепция, терминология и измерение
- 2. В медицине и здравоохранении часто используются, сознательно
- 3. Вероятностная природа медицины делает очевидной необходимость хорошего
- 4. Концепция «медицины, основанной на доказательствах» (evidence-based medicine,
- 5. Целью данного курса является помочь обучающимся в
- 6. Статистика – наука, изучающая количественные закономерности материальных
- 7. Статистика – · это инструмент для
- 8. Вероятностная природа медицины и вероятностный характер процессов
- 9. Основным инструментом для этого является теория вероятностей – математическая наука, устанавливающая закономерности случайных явлений.
- 10. Вероятность – количественная мера объективной возможности появления
- 11. Случайное событие –
- 12. В медицинских исследованиях достаточной считается вероятность появления
- 13. Частота появления события (статистическая вероятность) –
- 14. Шанс – это отношение вероятности того, что
- 15. Отношение шансов (odds ratio) – это отношение
- 16. Правило сложения вероятностей Если два события , А
- 17. Например: Вероятность того, что у взрослого человека все
- 18. Правило умножения вероятностей: Если два события, А и
- 19. Например: Какова вероятность того, что у 2-х не
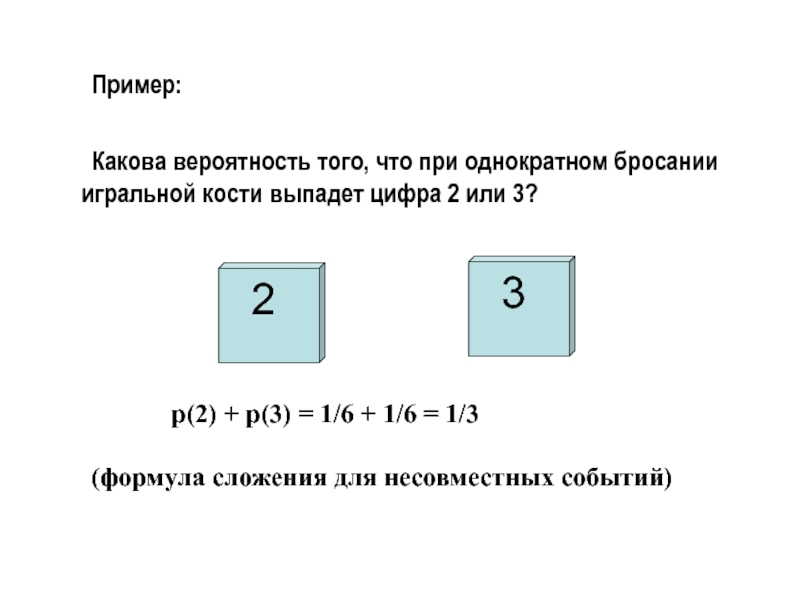
- 20. Пример: Какова вероятность того, что при однократном бросании
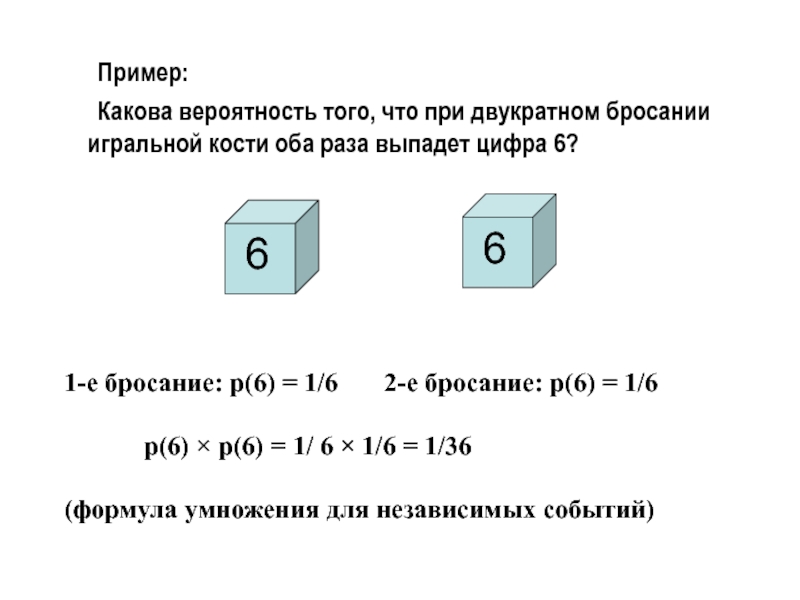
- 21. Пример: Какова вероятность того, что при двукратном бросании
- 22. Случайная величина – величина, которая при реализации определенного комплекса условий может принимать различные значения.
- 23. Закон больших чисел: при достаточно большом
- 24. Приступая к изучению основ статистического анализа необходимо
- 25. Основные направления применения математико-статистических методов в медицине
- 26. Прежде чем приступить к анализу данных и
- 27. Анализ организации конкретного исследования и его результатовОценить
- 28. Наиболее распространенные причины отказа в публикацииТема исследования
- 29. Из заключительного слова Т.Д.Лысенко на печально известной
- 30. Один из таких примеров мы можем найти
- 31. Знание возможностей статистических методов необходимо каждому работающему в медицине и здравоохранении.
- 32. Пакеты прикладных программSPSS (SPSS Inc.,USA)SASSTATASTATISTICA (StatSoft, USA;
- 33. SPSS - Statistical Package for Social Science - Статистический пакет для социальных наук
- 34. Скачать презентанцию
В медицине и здравоохранении часто используются, сознательно или неосознанно, различные статистические концепции при принятии решений по таким вопросам как - оценка состояния здоровья его прогноз; - выбор
Слайды и текст этой презентации
Слайд 3Вероятностная природа медицины делает очевидной необходимость хорошего знания соответствующих методов
решения проблем, связанных с неоднородностью и неопределенностью.
Слайд 4 Концепция «медицины, основанной на доказательствах» (evidence-based medicine, EBM) предполагает, что
к широкому применению в медицинской практике должны рекомендоваться те вмешательства,
эффективность и безопасность которых подтверждена в высококачественных исследованиях, выполненных на основе единых методологических принципов.Слайд 5Целью данного курса является помочь обучающимся в овладении наиболее часто
встречающимися методами и подходами статистического анализа и попытка предупредить наиболее
распространенные ошибкиСлайд 6Статистика – наука, изучающая количественные закономерности материальных явлений в неразрывной
связи с их качественной стороной. Биостатистика - приложение общей теории статистики
для решения научно-практических проблем в области биологии, медицины и здравоохранения. Медицинская (отраслевая) статистика: · Статистика здоровья населения · Статистика системы здравоохраненияСлайд 7Статистика – · это инструмент для анализа экспериментальных данных и результатов
популяционных исследований; · это язык, с помощью которого исследователь сообщает
полученные им результаты и благодаря которому он понимает медико-статистическую информацию; · это элемент доказательной медицины; · это база для обоснования принятия управленческих решений.Слайд 8 Вероятностная природа медицины и вероятностный характер процессов в общественном здоровье
позволяют повсеместно применять методы математической статистики и теории вероятностей и
выбирать их в зависимости от уровня решаемых задач с целью сведения к минимуму набора и степени проявления случайностей.Слайд 9Основным инструментом для этого является теория вероятностей – математическая наука,
устанавливающая закономерности случайных явлений.
Слайд 10 Вероятность – количественная мера объективной возможности появления события при реализации
определенного комплекса условий. Вероятность события А обозначается как р(А) и
выражается в долях единицы или в процентах. Мера вероятности – диапазон ее числовых значений: от 0 до 1 или от 0 до 100%.Слайд 11 Случайное событие – событие, которое при реализации определенного комплекса условий
может произойти или не произойти. Его вероятность будет находиться в
пределах 0< p(A) < 1 или 0< p(A) < 100%. Достоверное событие - событие, которое при реализации определенного комплекса условий произойдет непременно. Его вероятность будет равна 1 или 100%. Невозможное событие - событие, которое при реализации определенного комплекса условий не произойдет никогда. Его вероятность будет равна 0.Слайд 12 В медицинских исследованиях достаточной считается вероятность появления события не менее
0,95 или 95%. При изучении заболеваний или ситуаций, имеющих важнейшие
медико-социальные последствия или высокие показатели летальности и инвалидности, а также при фармакологических исследованиях вероятность появления события должна быть не менее 0,99 (99%).Слайд 13Частота появления события (статистическая вероятность) – это отношение числа случаев,
в которых реализовался определенный комплекс условий (m), к общему числу
случаев (n): p(A)=m/n. Вероятность отсутствия события: q= 1- p. Например, если вероятность того, что больной останется жив спустя пять лет после операции равна 0.8 (80%), то вероятность того, что он за этот временной промежуток умрёт равна 0.2 (20%).Слайд 14 Шанс – это отношение вероятности того, что события произойдёт к
вероятности того, что событие не произойдёт.
В нашем примере шанс
равен 4, так как 0.8/0.2=4Таким образом, вероятность выздоровления в 4 раза больше вероятности смерти.
Интерпретация:
1) Если Шанс =1, то вероятность наступления события равна вероятности того, что событие не произойдёт;
2) если Шанс >1, то вероятность наступления события больше вероятности того, что событие не произойдёт;
3) если Шанс <1, то вероятность наступления события меньше вероятности того, что событие не произойдёт.
Слайд 15 Отношение шансов (odds ratio)
– это отношение шансов для первой
группы объектов к отношению шансов для второй группы объектов.
Допустим, что некоторое лечение проходят и мужчины, и женщины. Вероятность того, что больной мужского пола останется жив спустя пять лет после лечения равна 0.6 (60%); вероятность того, что он за этот временной промежуток умрёт равна 0.4 (40%). Аналогичные вероятности для женщин
равны 0.8 и 0.2.
Отношение шансов в этом примере равно
Интерпретация:
1) Если отношение шансов =1, то шанс для первой группы равен шансу для второй группы
2) Если отношение шансов >1, то шанс для первой группы больше шанса для второй группы
3) Если отношение шансов <1, то шанс для первой группы меньше шанса для второй группы
Слайд 16Правило сложения вероятностей
Если два события , А и В, взаимоисключающие,
несовместимые, то вероятность события А или В равна сумме их
вероятностей:Р(А или В) = р(А) + р(В)
Слайд 17Например:
Вероятность того, что у взрослого человека все зубы сохранены –
0,67;
Вероятность отсутствия некоторых зубов – 0,24;
Вероятность того, что он –
беззубый – 0,09.Какова вероятность того, что у взрослого человека есть хотя бы несколько зубов?
0,67 + 0,24 = 0,91
Слайд 18 Правило умножения вероятностей:
Если два события, А и В, независимы (т.е.
возникновение одного события не влияет на возможность появления другого), то
вероятность того, что оба события произойдут, равна произведению вероятности каждого:Р(А и В) = р(А) × р(В)
Слайд 19 Например:
Какова вероятность того, что у 2-х не имеющих отношения друг
к другу больных, ожидающих приема к стоматологу, есть все зубы?
0,67
× 0,67 = 0,45Слайд 20 Пример:
Какова вероятность того, что при однократном бросании игральной кости выпадет
цифра 2 или 3?
или
3
2
р(2) + р(3) = 1/6
+ 1/6 = 1/3(формула сложения для несовместных событий)
Слайд 21 Пример:
Какова вероятность того, что при двукратном бросании игральной кости оба
раза выпадет цифра 6?
6
6
1-е бросание: р(6) = 1/6
2-е бросание: р(6) = 1/6р(6) × р(6) = 1/ 6 × 1/6 = 1/36
(формула умножения для независимых событий)
Слайд 22Случайная величина – величина, которая при реализации определенного комплекса условий
может принимать различные значения.
Слайд 23Закон больших чисел: при достаточно большом числе наблюдений случайные отклонения
взаимно погашаются и проявляется основная тенденция (закономерность).
Слайд 24Приступая к изучению основ статистического анализа необходимо выделить два основных
его этапа: · Описание полученного в ходе исследования массива данных · Анализ данных
и проверка различных статистических гипотезСлайд 25Основные направления применения математико-статистических методов в медицине и здравоохранении: 1) Наиболее эффективный
сбор данных и обобщение полученных результатов; 2) Сравнение и определение достоверности различия
двух и более групп результатов; 3) Изучение взаимосвязи между факторами и явлениями; 4) Анализ динамики процессов; 5) Анализ прогностических факторов.Слайд 26 Прежде чем приступить к анализу данных и проверке различных гипотез: 1.
Сформулируйте вопрос, на который Вы хотите ответить с помощью статистического
анализа. 2. Выберите наиболее адекватный для ответа на данный вопрос статистический критерий или метод. 3. Правильно интерпретируйте его результаты.Слайд 27Анализ организации конкретного исследования и его результатов
Оценить адекватность дизайна научного
исследования решению той или иной проблемы эпидемиологии и общественного здоровья.
Анализ
технологии приведенного исследования.Оценка полученных результатов.
Практическое применение полученных результатов.
Слайд 28Наиболее распространенные причины отказа в публикации
Тема исследования не представляет научного
интереса
Исследование неоригинально, т.е. кто-то провел уже такое же или похожее
исследованиеАвторская гипотеза на самом деле в статье не проверяется
Исследование было неправильно организовано
Выборка участников исследования слишком мала
В исследовании не было контрольной группы или она не соответствовала его целям
Статистический анализ проведен неправильно
Выводы авторов не основываются на результатах исследования
Статья так плохо написана, что ее никто не понимает
Trisha Greenhalgh “How to read a paper”
Слайд 29Из заключительного слова Т.Д.Лысенко на печально известной сессии ВАСХНИЛ:
«…Теория вероятностей
и статистика нужны только менделистам-морганистам, а "мичуринской биологии" эти науки
не нужны.»«… Изживая из нашей науки менделизм-морганизм-вейсманизм, мы тем самым изгоняем случайность из биологической науки. Нам необходимо твердо запомнить, что наука - враг случайностей ".
Эта фраза Лысенко на долгие годы стала одной из методологических заповедей биомедицины. Ученым, которые отваживались применять статистику в своих биомедицинских исследованиях, ВАК даже отказывал в ученой степени.
Слайд 30 Один из таких примеров мы можем найти в статье секретаря
Фрунзенского райкома ВКП(б) Москвы Е. Фурцевой (будущего министра культуры СССР)
“Партийное руководство научными учреждениями” опубликованной в газете “Правда” от 3 августа 1949 г.:“Ученый совет 1 Московского медицинского института утвердил две диссертации — одну на соискание ученой степени кандидата наук (Г.Л.Лемперта), другую — на степень доктора медицинских наук (Г.П.Сальниковой). Авторы некритически использовали данные лживой, тенденциозной буржуазной статистики и пришли к чудовищно извращенным, лженаучным выводам. Однако коммунисты — члены Ученого совета 1 Московского медицинского института — прошли мимо лженаучных утверждений “диссертантов” и голосовали за присвоение им ученых степеней. И правильно решила Высшая аттестационная комиссия Министерства высшего образования СССР, отказав соискателям в присвоении ученых степеней”.
www.biometrica.tomsk.ru