Волновые Пакеты

h/λ. Однако импульс принято выражать не через длину волны λ,

а через волновое число k ≡ 2π/λ:

Величина h/(2π) встречается столь часто, что для нее введено специальное обозначение ħ («аш» перечеркнутое):

Рассмотрим движущуюся вдоль оси х частицу, длина волны которой в точности равна λ0. Волновое число частицы k0 = 2π/λ0.
В качестве волновой функции следует взять

Сама ψ представляет собой волну, распространяющуюся в положительном направлении оси х. Распределение вероятностей обнаружить частицу

p = ħk – соотношение де Бройля.

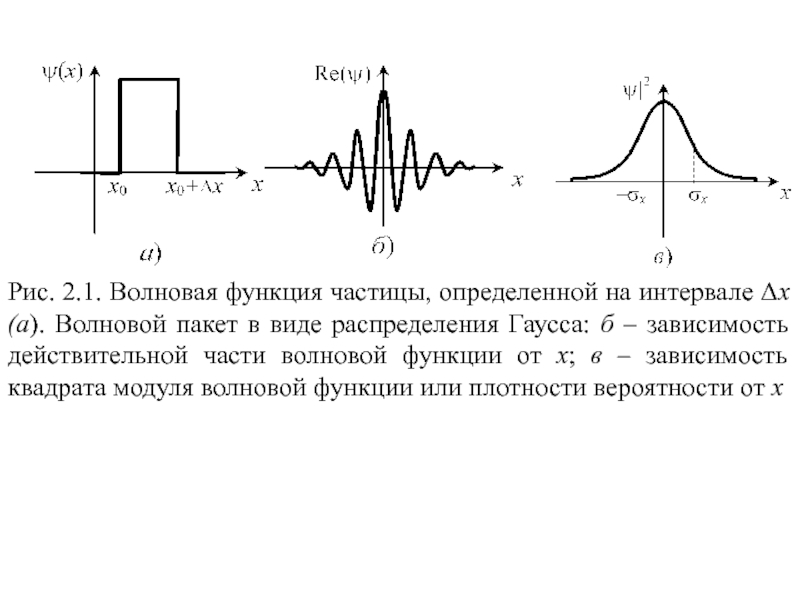
2.1. Волновые пакеты

волнами:
Re (ψ) = A cos (k0 x – ωt)

Im (ψ) = A sin (k0 x – ωt).
Таким образом, если импульс частицы имеет определенное значение, то она с равной вероятностью может находиться в любой точке пространства. Иначе говоря, если импульс частицы точно известен, то мы ничего не знаем о ее местонахождении.

не зависит от х и t – частица может быть обнаружена с равной вероятностью в любой точке на оси х (учтено, что еia⋅е−ia = 1). Использование комплексной волновой функции дает равномерное распределение вероятностей по оси х. Из формулы Эйлера

Волновой пакет в виде распределения Гаусса: б – зависимость действительной

части волновой функции от х; в – зависимость квадрата модуля волновой функции или плотности вероятности от х

в определенной области пространства.
Выясним теперь, какие волны следует сопоставлять частицам,

наблюдаемым в обычных, классически поставленных опытах. Классические опыты всегда начинаются с того, что мы определяем положение частицы в некоторый момент времени t = 0. Пусть измерение координаты проделано с точностью Δх, т.е. мы однозначно определили, что частица находится между х0 и х0 + Δх. С точки зрения волновой (квантовой) теории это означает, что волновая функция частицы равна нулю во всем пространстве, кроме участка, заключенного между х0 и х0 + Δх, рис. 2.1,а. Ясно, что такая функция не является одной монохроматической волной де Бройля типа

t = 0 зависимость волн де Бройля от времени является

пока несущественной. Запишем отдельную волну в виде

Изображенная на рисунке 2.1,а ψ-функция может быть представлена по теореме Фурье в виде бесконечной совокупности таких волн в виде интеграла Фурье

, где B = Ae−iωt.

Таким образом, состояние частицы в начальный момент времени определяется, наложением большого числа монохроматических волн, каждая из которых движется со своей скоростью (импульсом).

волновым пакетом. Во всякий другой момент времени положение частицы описывается,

грубо говоря, местоположением максимума ψ-функции. Рассмотрим волновую функцию вида:

в момент времени t = 0.
На рис. 2.1,б приведена действительная часть этой волновой функции,

функция частицы, определенной на интервале Δх (а). Волновой пакет в

виде распределения Гаусса: б – зависимость действительной части волновой функции от х; в – зависимость квадрата модуля волновой функции или плотности вероятности от х

от х = – σх до х = +σх. Функция

ехр(–х2/2σх2) – это известное распределение Гаусса; здесь σх – среднеквадратичное отклонение, которое назовем неопределенностью величины х и обозначим Δх. Локализованная волна называется волновым пакетом. Изображенная на рис. 2.1,б волна естественно не является чисто монохроматической. Волновой пакет можно представить в виде суммы (суперпозиции) плоских монохроматических волн с близкими значениями частот (ω) и волновых векторов (k).

Для иллюстрации рассмотрим волновой пакет в момент времени t = 0 и подберем подходящую суперпозицию монохроматических, волн типа exp(ikx). Для этого требуется найти коэффициенты Bn в выражении

мы перейдем от суммирования к интегрированию:

Используя тождество

получаем

Заменив k на р/ħ,

найдем коэффициент В в импульсном представлении

случая двух волновых пакетов различной ширины. Отметим, что чем ýже

волновой пакет, тем шире распределение по импульсам. Вероятность найти частицу в состоянии с волновой функцией В(k)⋅exp(ikx) пропорциональна квадрату ее амплитуды, вероятность различных значений импульса определяется функцией

Распределение |В(р)|2 является Гауссовым для р, и его можно переписать в виде

ей волновой пакет (внизу). Ширина волнового пакета (а) вдвое превышает

его ширину (б). В обоих случаях заметим, что произведение σхσp одно и то же

Здесь σр – среднеквадратичное отклонение или «неопределенность» величины р. Из двух последних соотношений следует
σp = ħ/2σx, σpσх = ħ/2,

Таким образом, в случае волновой функции в виде распределения Гаусса произведение ширины волнового пакета на ширину функции распределения по импульсам равно ħ/2. В других случаях это произведение может быть больше ħ/2, !!!но оно никогда не будет меньше ħ /2!!!. В общем случае

не порознь на Δх или на Δрх, а лишь на

их произведение − Δх⋅Δрх.

*) Как будет показано ниже, соотношение Δх⋅Δрх ≥ ħ/2, полученное для гауссова распределения, может быть записано в форме: Δх⋅Δрх ≥ ħ или Δх⋅Δрх ≥ h. Последняя форма записи используется в квантовых статистиках, например, Ферми-Дирака или Бозе-Эйнштейна.

Соотношение или принцип неопределенностей утверждает, что если частица локализована в пространстве со среднеквадратичным отклонением Δх, то ее импульс не имеет определенного значения, а характеризуется распределением |В(р)| с «шириной» Δр. Физически это означает, что невозможно одновременно точно определить значения координаты и импульса частицы.

В качестве примера рассмотрим волновой пакет с распределением по импульсам в виде прямоугольника, показанного на рис. 2.3,а:

координаты, измеренная на уровне половины максимального значения, и Δр –

то же самое для импульса).

Рис. 2.3. Прямоугольное распределение по импульсам (а); б – распределение по координатам, или волновой пакет, соответствующий распределению на (a)

находим

Эта функция уменьшается вдвое при аx = 1,39. Следовательно
аΔх = 1,39.
Поскольку a = Δk = Δрх/ħ, то (Δрх/ħ)Δх = 1,39.
Таким образом, Δх∙Δрх = 1,39ħ, т.е.
Δх∙Δрх ≥ ħ

= 0. Можно попытаться с помощью микроскопа определить положение частицы

и тем самым обойти принцип неопределенности. Микроскоп позволит определить положение частицы с точностью до длины волны используемого света, Δх ≈ λ . Но поскольку Δр = 0, то произведение Δ·Δрх также должно быть равно нулю, и принцип неопределенности, казалось бы, нарушится. Но это не так. Мы пользуемся светом, a свет состоит из фотонов с импульсом р = h/λ. Чтобы обнаружить частицу, на ней должен рассеяться или поглотиться по крайней мере один из фотонов пучка света (рис. 2.4), и частице будет передан импульс, достигающий h/λ. Таким образом, в момент наблюдения положения частицы с точностью Δх ≈ λ неопределенность ее импульса Δрх ≥ h/λ. Перемножая неопределенности Δрх и Δх, находим

квантовой механики.
Рис. 2.4. Взаимодействие в микроскопе фотонов с частицей

приводит к неопределенности ее импульса в момент наблюдения на Δр≥ h/λ

Двойственная корпускулярно-волновая природа микрочастиц накладывает ограничения на точность определения физических величин, характеризующих состояние частицы. Причем эти ограничения никак не связаны с точностью измерений, достижимой в конкретном эксперименте, а имеют принципиальное значение.

одновременного определения канонически сопряженных динамических переменных, характеризующих квантовую систему: координата

– импульс, действие – угол и т.д. Математически соотношения неопределенностей имеют вид неравенства, например:

Δх∙рх ≥ ħ/2

где Δх и Δрх – неопределенности значений координаты х и сопряжённой ей компоненты рх импульса р (аналогичные соотношения справедливы и для пар других компонент координаты и импульса: y, рy; z, рz). Соотношения неопределенностей были установлены В. Гейзенбергом (W. Heisenberg) в 1927 г.