Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вписанная и описанная окружности
Содержание
- 1. Вписанная и описанная окружности
- 2. ПовторяемКак найти центр вписанной окружности?Как найти центр
- 3. Докажите, что радиус окружности, вписанной в прямоугольный
- 4. Докажите, что если центр окружности, описанной около
- 5. Задачи для самостоятельного решенияВ ∆АВС А =30°,
- 6. Поздравляем! Вы выполнили задания, соответствующие минимальным
- 7. В прямоугольном треугольнике точка касания вписанной окружности
- 8. Поздравляем! Вы выполнили задания среднего уровня.
- 9. Периметр ∆АВС равен 58 см. D,E, F
- 10. Урок окончен, до свидания. Выучите теоремы
- 11. Скачать презентанцию
ПовторяемКак найти центр вписанной окружности?Как найти центр описанной окружности?Какие свойства окружности мы знаем?Сформулируйте свойство касательной к окружности.Сформулируйте признак касательной к окружности.
Слайды и текст этой презентации
Слайд 2Повторяем
Как найти центр вписанной окружности?
Как найти центр описанной окружности?
Какие свойства
окружности мы знаем?
окружности.
Слайд 3Докажите, что радиус окружности, вписанной в прямоугольный треугольник, вычисляется по
формуле r = ½(a + b – c), где а
и b – катеты, а с – гипотенуза. Док-во: Пусть М – точка касания окружности и стороны ВС, тогда радиус ОМВС, ОС – биссектриса С, т.к. центр вписанной окружности лежит на пересечении биссектрис.
Дано: ∆АВС, С = 90°, О – центр вписанной окружности, r – радиус вписанной окружности.
Док-ть r = ½(a + b – c).
С
А
В
О
Стороны треугольника часто называют также, как противолежащие вершины, но обозначают маленькими буквами. Т.е. а = ВС, b = АС, с = АВ
М
Рассмотрим ∆СМО:
ВС = r + BM BM = BC – r = a - r, DC = CM = ОМ = r, т.к. DC и СМ – касательные, проведенные из одной точки,
AC = AD + DC = AD + r AD = AC – r = b – r,
ВЕ = ВМ(кас.), АЕ = AD (кас.) с = АВ = ВЕ + АЕ = ВМ + AD = a – – r + b – r = a + b – 2r = c, т.е. с = а + b – 2r. Выразим r.
2r = a + b – c, r = ½(a + b – c).
D
E
ОМС = 90°, ОСМ = ½АСВ = ½∙90° = 45°
СОМ = 180° - ОМС - ОСМ =
= 180° - 90° - 45° = 45°, ∆ СМО – р/б,
СМ = МО
СМ = ОМ
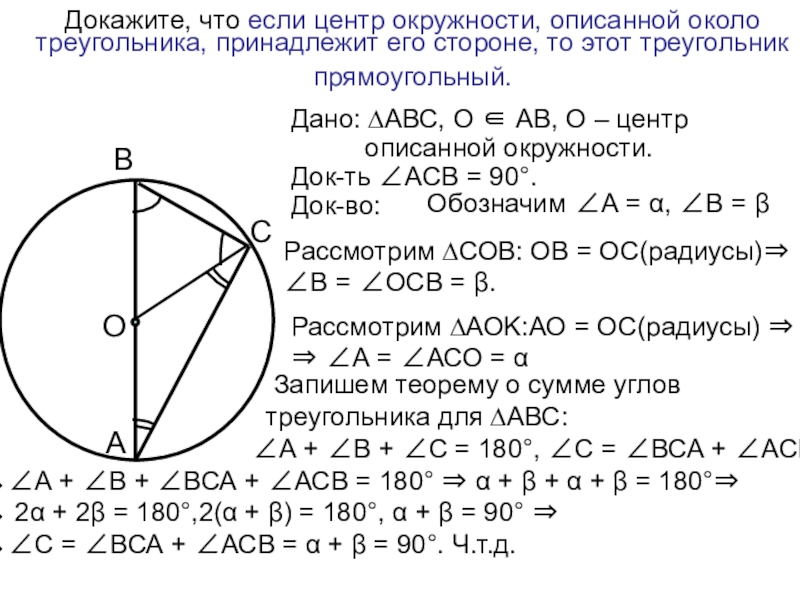
Слайд 4Докажите, что если центр окружности, описанной около треугольника, принадлежит его
стороне, то этот треугольник прямоугольный.
Обозначим А = α, В = βА
В
Дано: ∆АВС, О АВ, О – центр
описанной окружности.
Док-ть АСВ = 90°.
Док-во:
С
О
Рассмотрим ∆СОВ: ОВ = ОС(радиусы)
В = ОСВ = β.
Рассмотрим ∆АОK:АО = ОС(радиусы)
А = АСО = α
Запишем теорему о сумме углов
треугольника для ∆АВС:
А + В + С = 180°, С = ВСА + АСВ
А + В + ВСА + АСВ = 180° α + β + α + β = 180°
2α + 2β = 180°,2(α + β) = 180°, α + β = 90°
С = ВСА + АСВ = α + β = 90°. Ч.т.д.
Слайд 5Задачи для самостоятельного решения
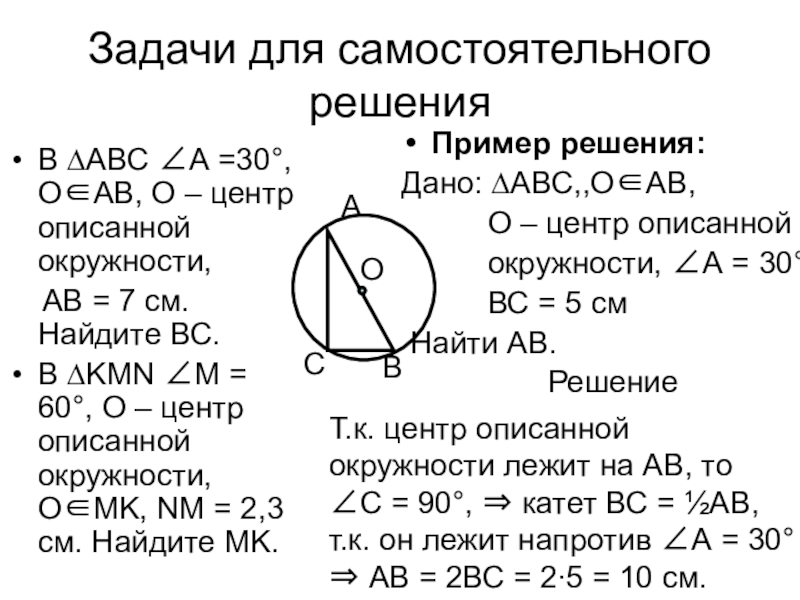
В ∆АВС А =30°, ОАВ, О –
центр описанной окружности,
АВ = 7 см. Найдите
ВС. В ∆KМN М = 60°, О – центр описанной окружности, ОМK, NМ = 2,3 см. Найдите МK.
Пример решения:
Дано: ∆АВС,,ОАВ,
О – центр описанной
окружности, А = 30°,
ВС = 5 см
Найти АВ.
Решение
С
В
А
О
Т.к. центр описанной
окружности лежит на АВ, то
С = 90°, катет ВС = ½АВ,
т.к. он лежит напротив А = 30°
АВ = 2ВС = 2∙5 = 10 см.
Слайд 6Поздравляем!
Вы выполнили задания, соответствующие минимальным программным требованиям.
(Максимальная
оценка 3)
Если выполненные задания показались вам сложными, нажмите кнопку «Закончить
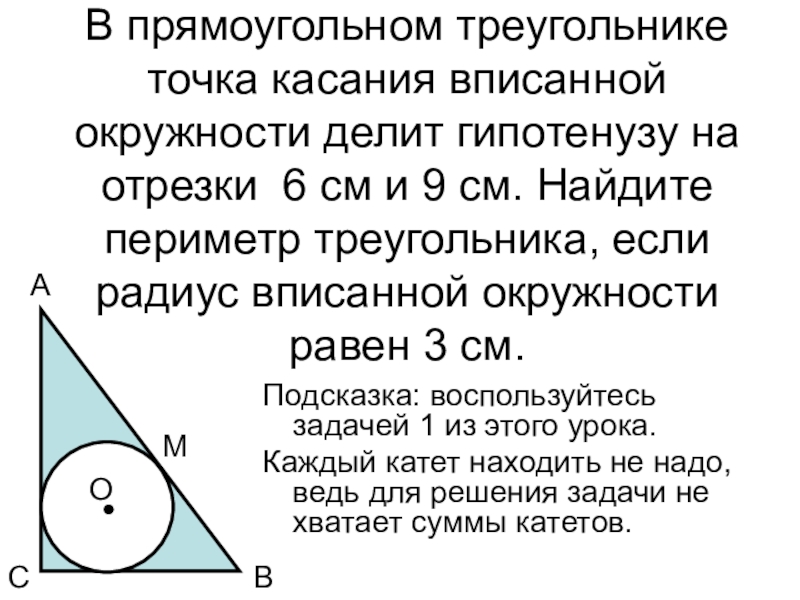
занятие»(►│). Если хотите повысить оценку, нажмите кнопку «Далее»(►).
Слайд 7В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на
отрезки 6 см и 9 см. Найдите периметр треугольника, если
радиус вписанной окружности равен 3 см.Подсказка: воспользуйтесь задачей 1 из этого урока.
Каждый катет находить не надо, ведь для решения задачи не хватает суммы катетов.
С
А
В
М
О
Слайд 8Поздравляем!
Вы выполнили задания среднего уровня.
(Максимальная оценка 4)
Если
выполненные задания показались вам сложными, нажмите кнопку «Закончить занятие»(►│). Если
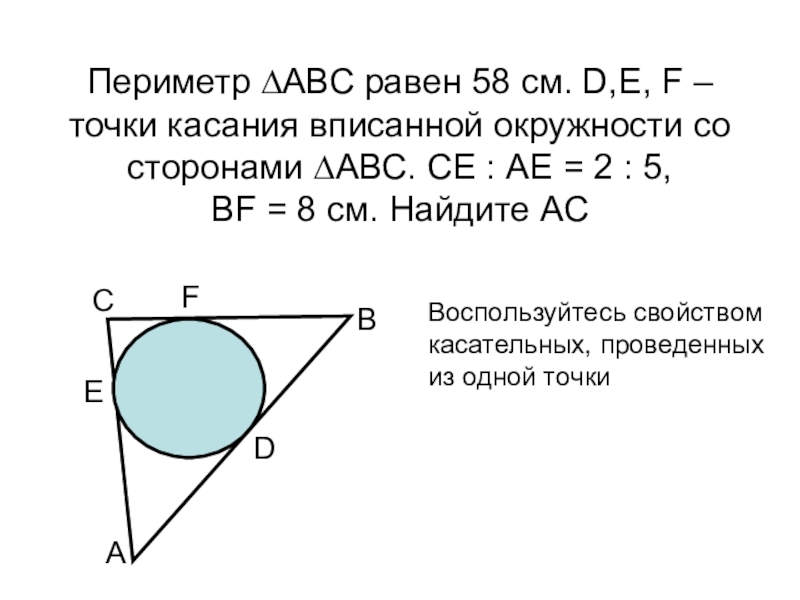
хотите повысить оценку, нажмите кнопку «Далее»(►).
Слайд 9Периметр ∆АВС равен 58 см. D,E, F – точки касания
вписанной окружности со сторонами ∆АВС. СЕ : АЕ = 2
: 5, BF = 8 см. Найдите АСА
В
С
D
F
Е
Воспользуйтесь свойством
касательных, проведенных
из одной точки
Слайд 10Урок окончен,
до свидания.
Выучите теоремы со слайдов 2 и
3.
Текст теорем выделен синим.
Не забудьте отправить файл со
сделанными заданиями в личные сообщения учителю.
