Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вступ до дискретної математики. Елементи і множини
Содержание
- 1. Вступ до дискретної математики. Елементи і множини
- 2. ЗмістВступ…………………………………………………. 3Множина. Елемент………………………………….. 4Способи задання множини …………………………..6Позначення часто використовуваних множин ……..7Рівні
- 3. ВступТеорія множин – це розділ математики, який
- 4. Алгебра множин — розділ теорії множин, який визначає закони
- 5. Множина. ЕлементМножина – будь-який набір певних відмінних
- 6. Про множину говорять, що вона містить елементи.Якщо
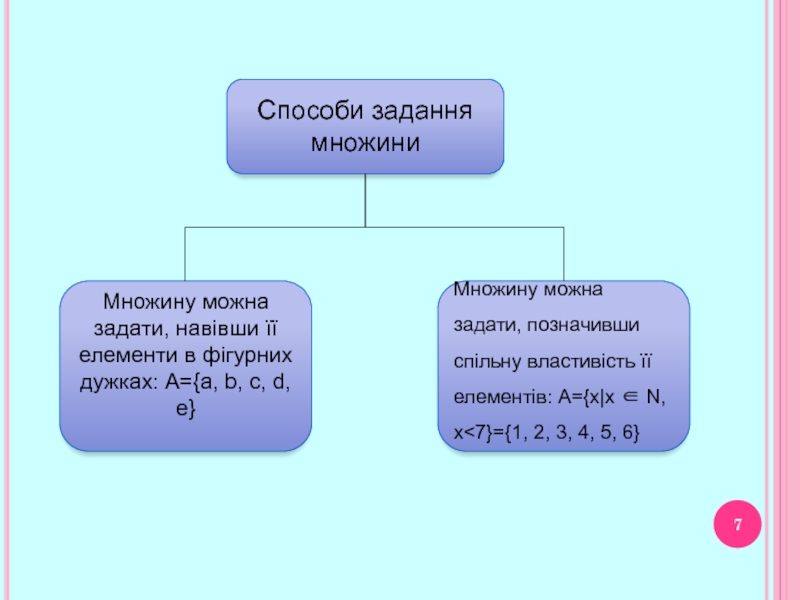
- 7. Слайд 7
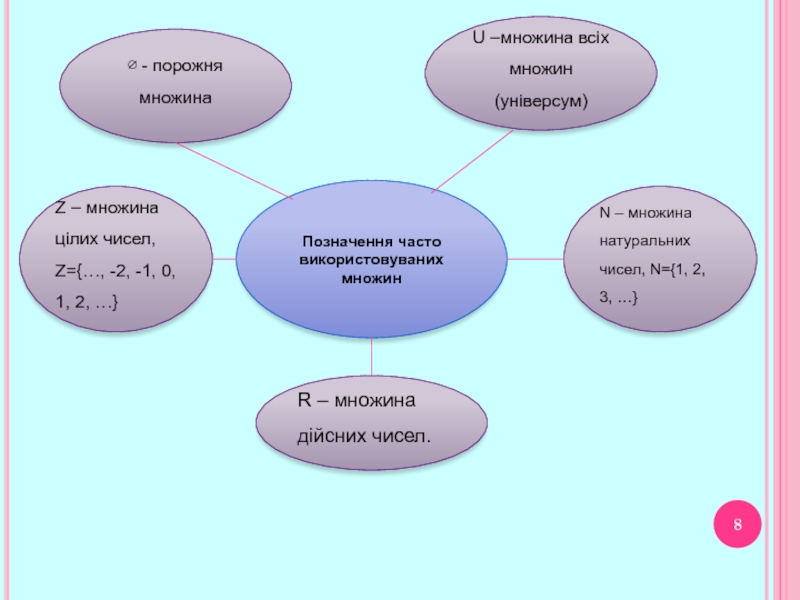
- 8. U –множина всіх множин (універсум)
- 9. Рівні множини Дві множини
- 10. Підмножина. Невласна підмножина Множину
- 11. Скінченні та нескінченні множини. Потужність
- 12. Універсальна множина Часто всі
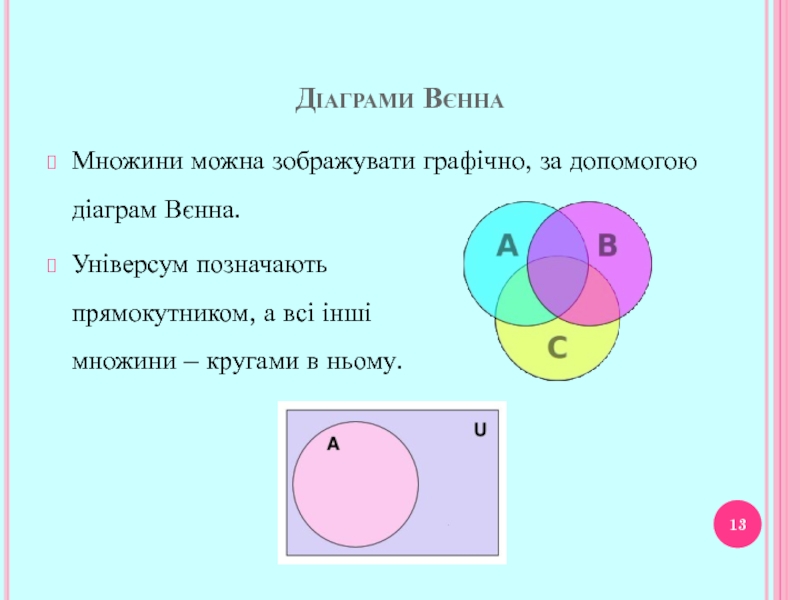
- 13. Діаграми Вєнна Множини можна
- 14. Булеан
- 15. Теоретико-множинні операції Для множин можна
- 16. Теоретико-множинні операціїОб’єднанням множин A і B (позначається A∪B ) називається множина тих елементів, які
- 17. Теоретико-множинні операціїПеретином множин A і B (позначається A∩B ) називається множина, що складається з
- 18. Теоретико-множинні операціїРізницею множин A і B (записується A\B ) називається множина тих елементів, які
- 19. Теоретико-множинні операціїДоповнення множиниЯкщо всі множини, які ми
- 20. Теоретико-множинні операції
- 21. Закони алгебри множин
- 22. Закони алгебри множин
- 23. Комп’ютерне подання множинУ комп’ютері можна подавати множини
- 24.
- 25. Двійкова система числення використовує для запису чисел тільки два
- 26. Слайд 26
- 27. ВисновкиОтже, множина – набір елементів. Про множину
- 28. Список літератури1. Нікольський Ю. В. Дискретна математика/
- 29. Скачать презентанцию
ЗмістВступ…………………………………………………. 3Множина. Елемент………………………………….. 4Способи задання множини …………………………..6Позначення часто використовуваних множин ……..7Рівні Множини ………………………………………..8Підмножина. Невласна підмножина ……………….9Скінченні та нескінченні множини. Потужність …10Універсальна Множина ……………………………..11Діаграми Вєнна ……………………………………12Булеан ………………………………………………...13Висновки …………………………………………....14Список літератури ……………………………….....15
Слайды и текст этой презентации
Слайд 2Зміст
Вступ…………………………………………………. 3
Множина. Елемент………………………………….. 4
Способи задання множини …………………………..6
Позначення часто використовуваних множин ……..7
Рівні Множини ………………………………………..8
Підмножина. Невласна підмножина
……………….9
Слайд 3Вступ
Теорія множин – це розділ математики, який вивчає загальні властивості
множин і є основою практично всіх математичних теорій, як "дискретних"
дисциплін комп'ютерного циклу, так і класичних "континуальних" розділів математики. Саме у термінах теорії множин проводиться розподіл математичних об'єктів і теорій на континуальні та дискретні.Слайд 4Алгебра множин — розділ теорії множин, який визначає закони композиції множин, виходячи з
основних властивостей операцій над ними, а також пропонує певну систематичну
процедуру для обчислення теоретико-множинних рівнянь та співвідношень.Слайд 5Множина. Елемент
Множина – будь-який набір певних відмінних один від одного
об’єктів нашої інтуїції чи інтелекту, розглядуваних як одне ціле.
Елементи –
об’єкти, що утворюють множину.Слайд 6Про множину говорять, що вона містить елементи.
Якщо a – елемент
множини A, то пишемо a ∈ A
Якщо ні – a ∉
AМножина не може містити двох однакових елементів, а порядок її елементів не фіксують.
Слайд 9Рівні множини
Дві множини називають рівними, якщо вони
складаються з одних і тих самих елементів
Позначають так: A=B
Слайд 10Підмножина. Невласна підмножина
Множину A називають підмножиною множини
B, якщо кожен елемент множини A належить множині B.
Позначають A
⊂ BЯкщо A = B або A = ∅ - то множину A називають невласною підмножиною множини B
Слайд 11Скінченні та нескінченні множини. Потужність
Множини бувають скінченні
та нескінченні.
Скінченною називають множину, для якої існує натуральне число, що
дорівнює кількості її елементів.Множину, що не є скінченною називають нескінченною.
Кільксть елементів скінченної множини називають потужністю і позначають як |A|.
Слайд 12Універсальна множина
Часто всі досліджувані множини являють собою
підмножини якоїсь множини, називаної універсальною множиною, або універсумом.
Універсальну множину позначають
як U.Слайд 13Діаграми Вєнна
Множини можна зображувати графічно, за допомогою
діаграм Вєнна.
Універсум позначають
прямокутником, а всі інші
множини – кругами
в ньому.Слайд 15Теоретико-множинні операції
Для множин можна ввести ряд операцій
(теоретико-множинних операцій), результатом виконання яких будуть також множини. За допомогою
цих операцій можна конструювати із заданих множин нові множини.Слайд 16Теоретико-множинні операції
Об’єднанням множин A і B (позначається A∪B ) називається множина тих елементів, які належать хоча б
одній з множин A чи B.
Приклад: {a,b,c}∪{a,c,d,e} = {a,b,c,d,e}
(a, b, c)
(a, c, d,
e)Слайд 17Теоретико-множинні операції
Перетином множин A і B (позначається A∩B ) називається множина, що складається з тих і тільки
тих елементів, які належать множинам A і B одночасно.
Приклад: {a,b,c}∩{a,c,d,e} = {a,c}
(a,b,c)
(a,c,d,e)
Слайд 18Теоретико-множинні операції
Різницею множин A і B (записується A\B ) називається множина тих елементів, які належать множині A і не
належать множині B.
Приклад:{a,b,c}\{a,d,c} = {b}
(a, b, c)
(a, d, c)
Слайд 19Теоретико-множинні операції
Доповнення множини
Якщо всі множини, які ми розглядаємо, є підмножинами
якоїсь так званої універсальної множини U, то різниця U\A називається доповненням множини A. Тобто доповненням множини A називається множина, яка
складається з усіх елементів, які не належать множині А (але які належать універсальній множині U). Доповнення множини A позначають так: Ā.Слайд 23Комп’ютерне подання множин
У комп’ютері можна подавати множини різними способами. Один
зі способів — зберігати невпорядковані елементи множини. Проте в такому
разі операції з множинами займатимуть багато часу через те, що потрібно щоразу переглядати елементи. Тому розглянемо інші способи. Одним із найпоширеніших і найпростіших способів — подання множин за допомогою бітових рядків. Упорядкуємо довільним способом елементи універсальної множини. Нехай універсальна множина U містить n елементів, тоді U = {a1, a2, a3, ..., a ₓ₋₁ − 1, a ₓ₋₁}. Множину A ⊂ U подають у комп’ютері рядком із 0 і 1 довжиною n так: якщо a ᵢ ∈ A, то i-й біт дорівнює 1, а ні, то 0.Слайд 25Двійкова система числення використовує для запису чисел тільки два символи, зазвичай 0
(нуль) та 1 (одиницю). Завдяки тому, що таку систему доволі
просто використовувати у електричних схемах, двійкова система отримала широке розповсюдження у світі обчислювальних пристроїв.Для переведення чисел із системи числення з основою p в систему числення з основою q з використанням арифметики старої системи числення з основою p потрібно: послідовно число, записане в системі основою p ділити на основу нової системи числення, виділяючи остачі. Останні записані у зворотному порядку, будуть утворювати число в новій системі числення.
Слайд 27Висновки
Отже, множина – набір елементів. Про множину кажуть що вона
містить елементи.
Є різні способи подання множин.
Універсальна множина містить всі інші
множини.Булеан – множина всіх підмножин заданої множини.