всех своих детей).
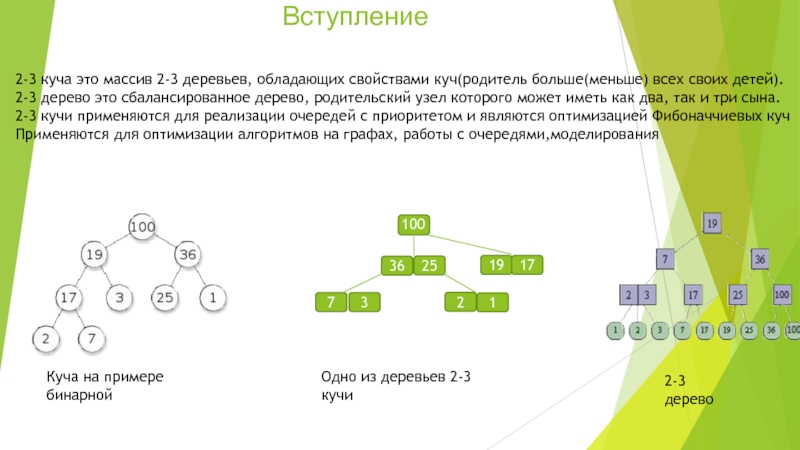
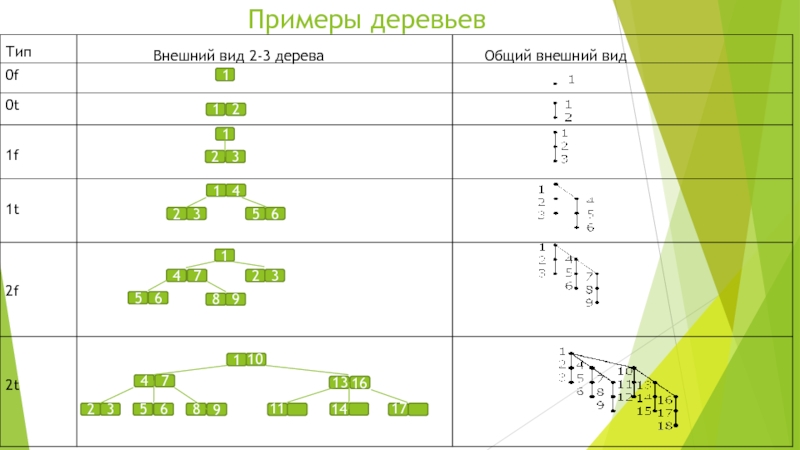
2-3 дерево это сбалансированное дерево, родительский узел которого
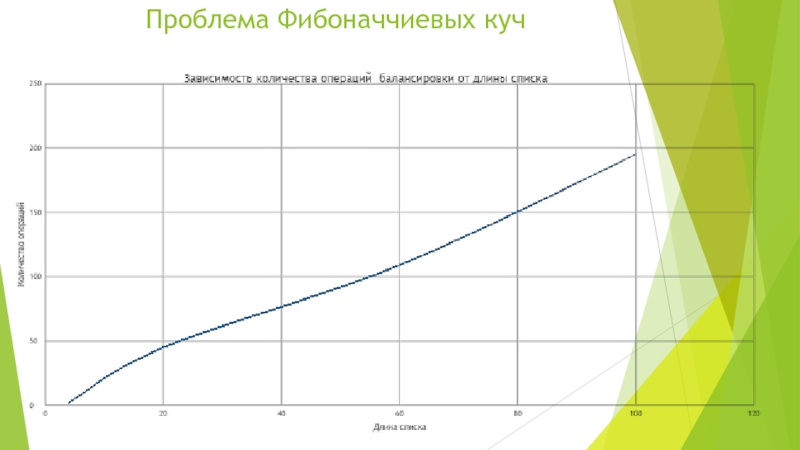
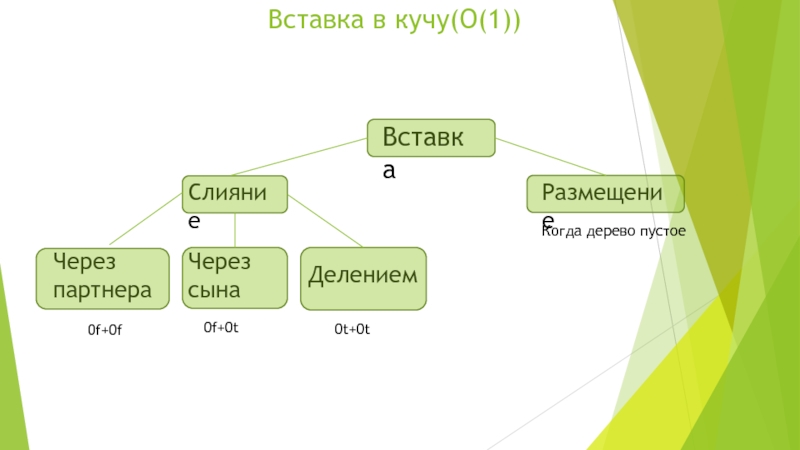
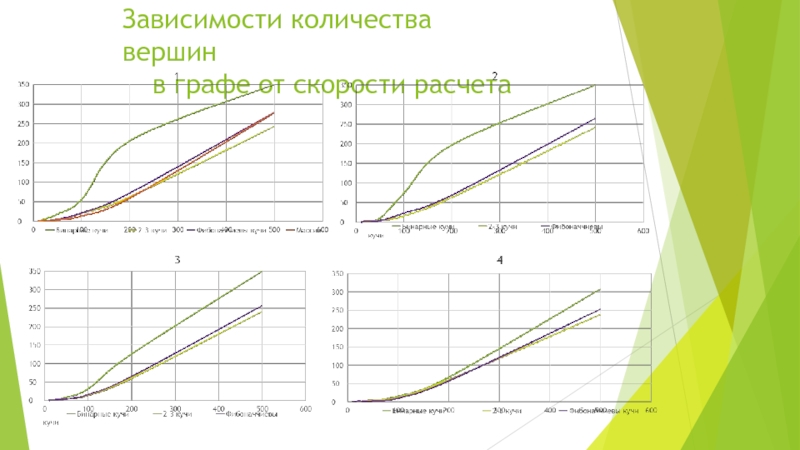
может иметь как два, так и три сына.2-3 кучи применяются для реализации очередей с приоритетом и являются оптимизацией Фибоначчиевых куч
Применяются для оптимизации алгоритмов на графах, работы с очередями,моделирования
Куча на примере бинарной
2-3 дерево
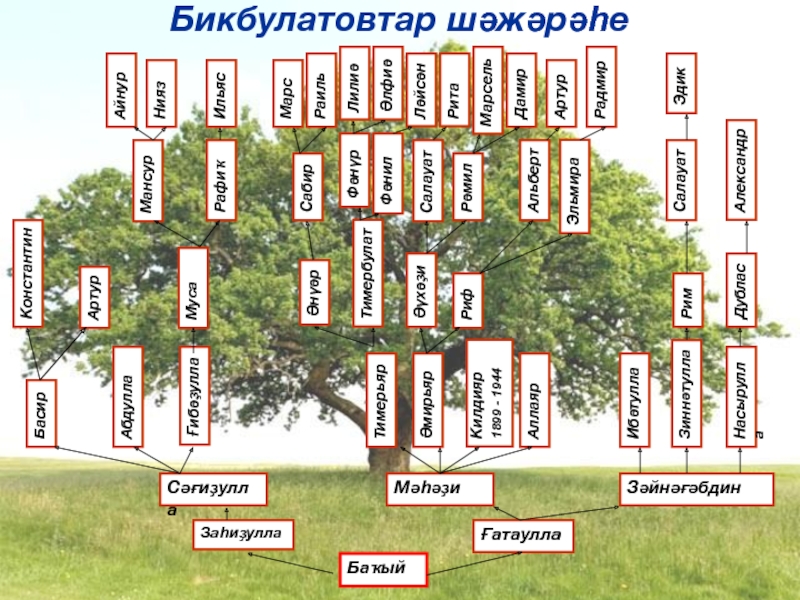
Одно из деревьев 2-3 кучи
36
25
19
17
7
3
2
1
100