Слайд 2Задача 1
Найти максимальное значение целевой функции
F = 4x1+3x2 → max,
при системе ограничений:
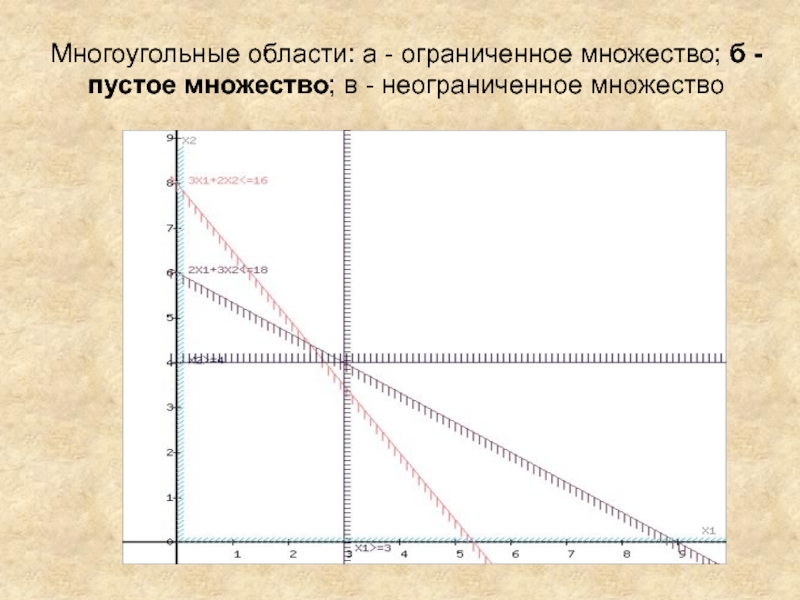
3x1+2x2≤16 (1)
2x1+3x2≤18 (2)
x1≥0 (3)
x2≥0 (4)
где x1, x1 - целые числа.
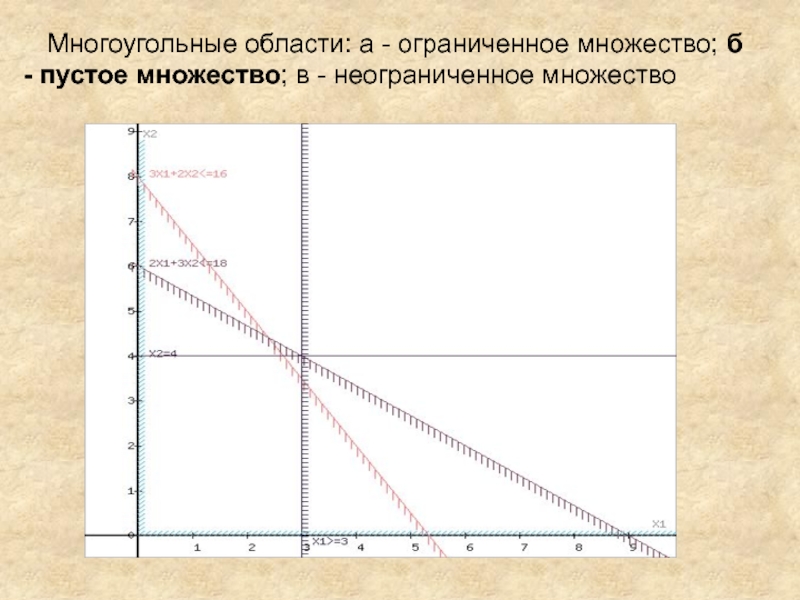
Построим область допустимых решений, т.е. решим графически систему неравенств (для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).
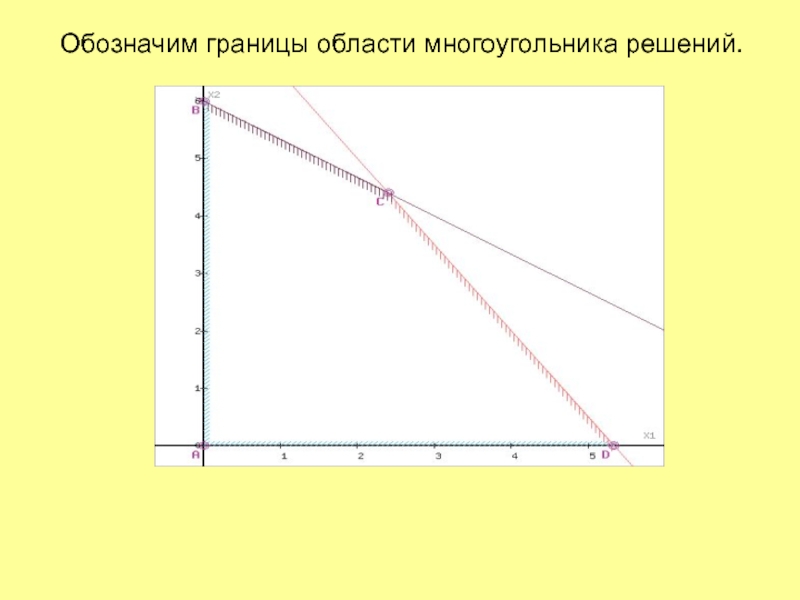
Слайд 4Обозначим границы области многоугольника решений.
Слайд 5Рассмотрим целевую функцию задачи
F = 4x1+3x2 → max.
Построим
прямую, отвечающую значению функции F = 0:
F = 4x1+3x2
= 0.
Поскольку нас интересует максимальное решение, поэтому будем двигать прямую параллельным образом до последнего касания обозначенной области.
На графике эта прямая обозначена пунктирной линией.
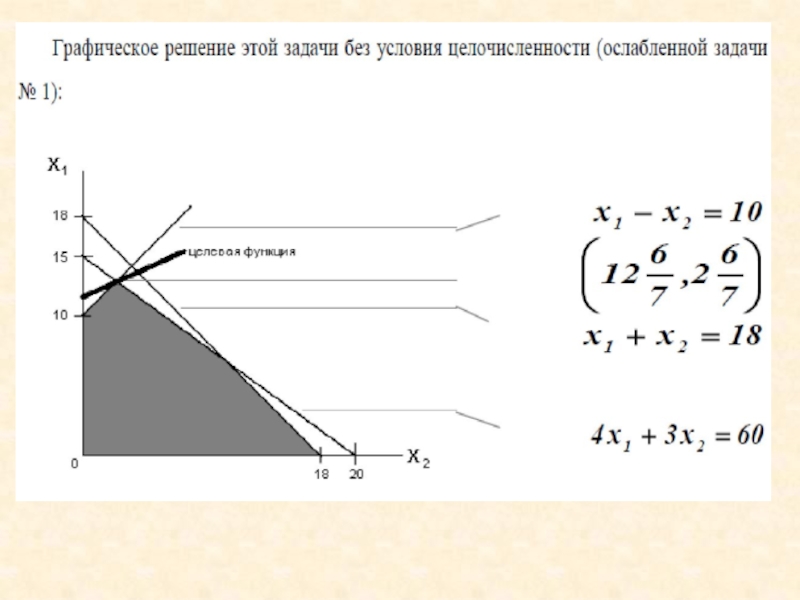
Слайд 7Область допустимых решений представляет собой многоугольник.
Прямая F(x) = const пересекает
область в точке C, которая получена в результате пересечения прямых
(1) и (2), то ее координаты удовлетворяют уравнениям этих прямых:
3x1+2x2≤16
2x1+3x2≤18
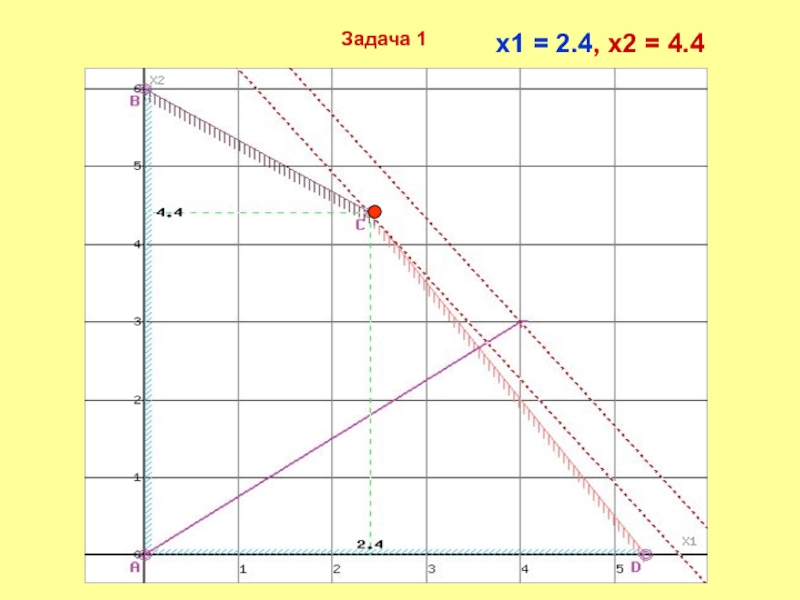
Решив систему уравнений, получим:
x1 = 2.4, x2 = 4.4
Откуда найдем максимальное значение целевой функции:
F(X) = 4*2.4 + 3*4.4 = 22.8
Оптимальное значение переменной x1=2.4 оказалось нецелочисленным.
Слайд 8Разбиваем задачу 1 на две подзадачи 11 и 12.
В первой
из них к условиям задачи 11 добавляется условие х1 ≥
3, а к задаче 12 — условие х1 ≤ 2.
Эта процедура называется ветвлением по переменной х1.
Решим графически задачу 11 как задачу ЛП.
3x1+2x2≤16 (1)
2x1+3x2≤18 (2)
x1≥3 (3)
x1≥0 (4)
x2≥0 (5)
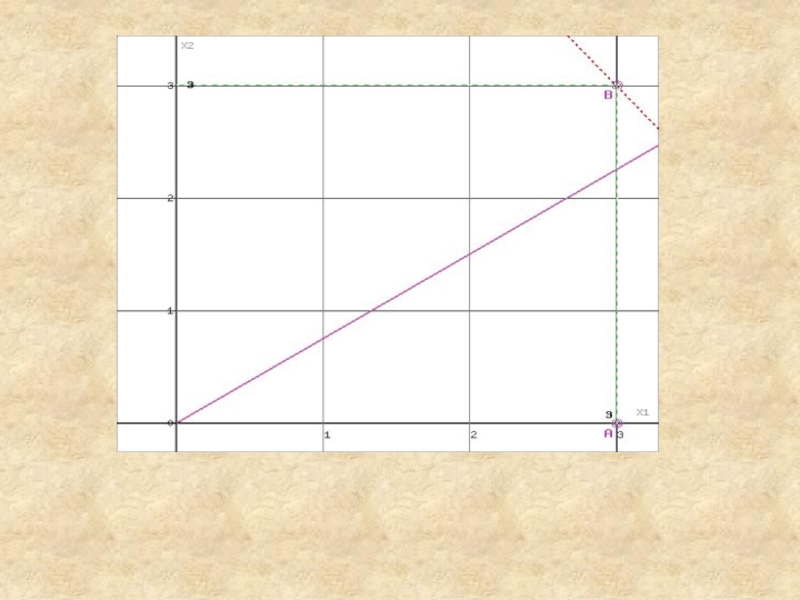
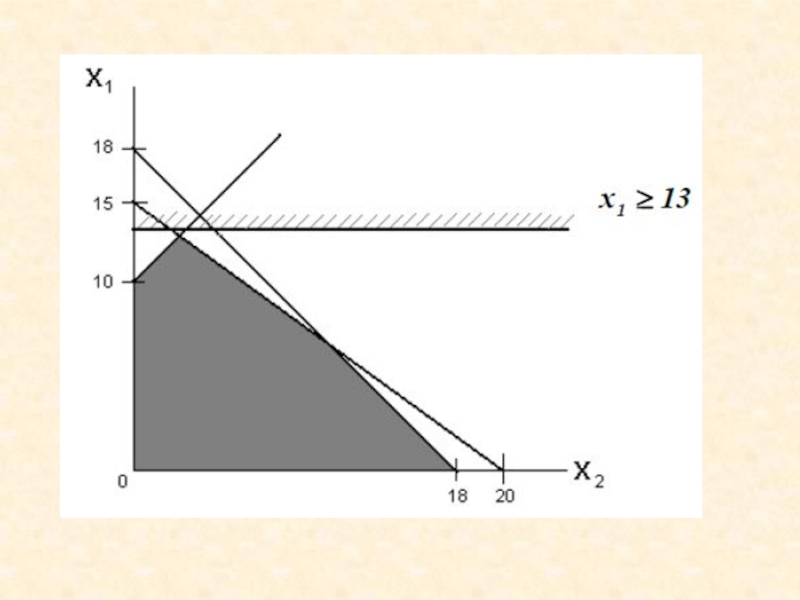
Область допустимых решений представляет собой треугольник.
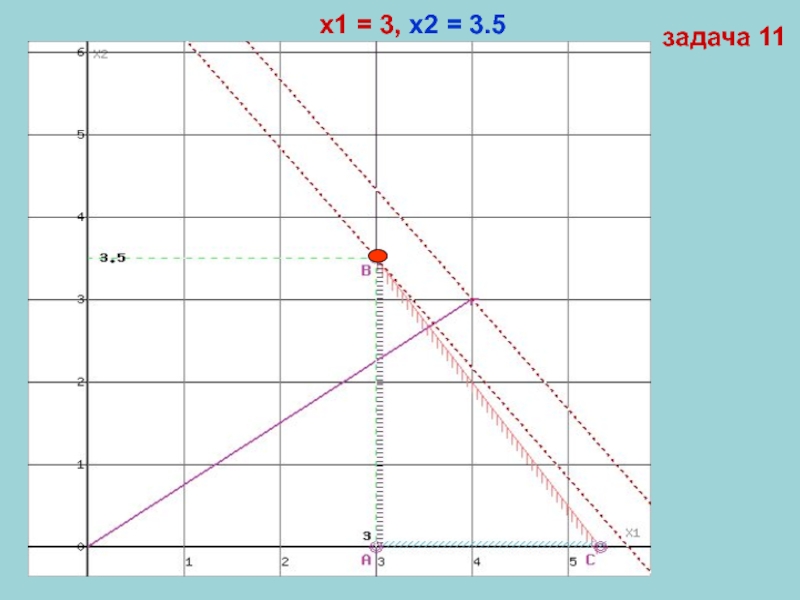
Слайд 9Прямая F(x) = const пересекает область в точке B. (получена
в результате пересечения прямых (1) и (3)), ее координаты удовлетворяют
уравнениям этих прямых:
3x1+2x2≤16
x1≥3
Решив систему уравнений, получим: x1 = 3, x2 = 3.5
Откуда найдем максимальное значение целевой функции:
F(X) = 4*3 + 3*3.5 = 22.5
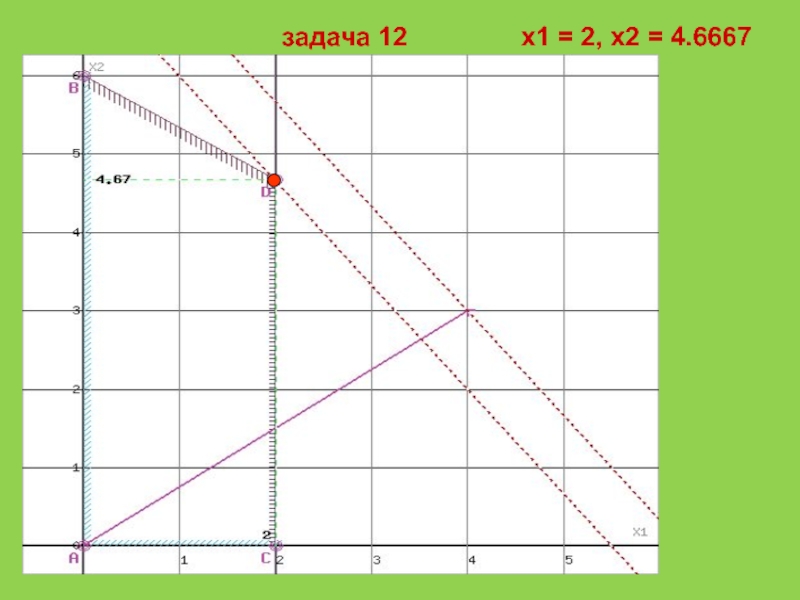
Слайд 11Решим графически задачу 12 как задачу ЛП.
3x1+2x2≤16 (1)
2x1+3x2≤18 (2)
x1≤2 (3)
x1≥0 (4)
x2≥0 (5)
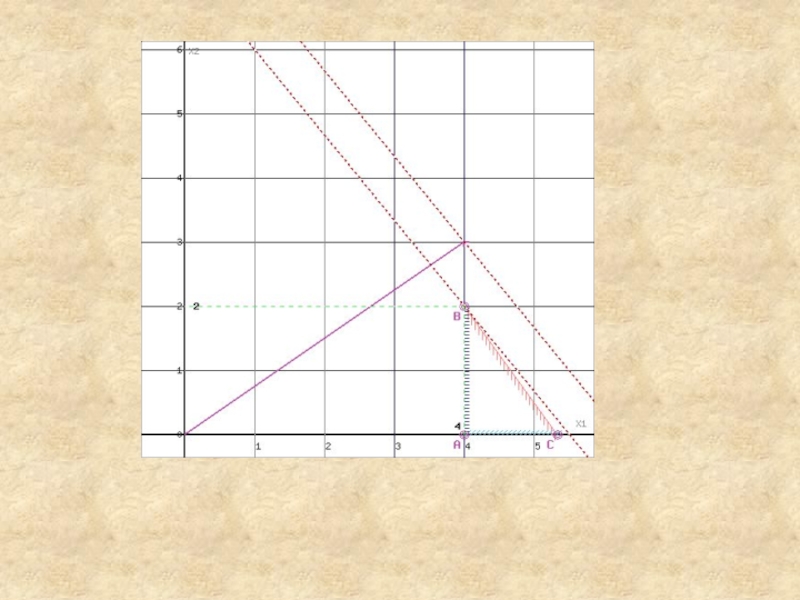
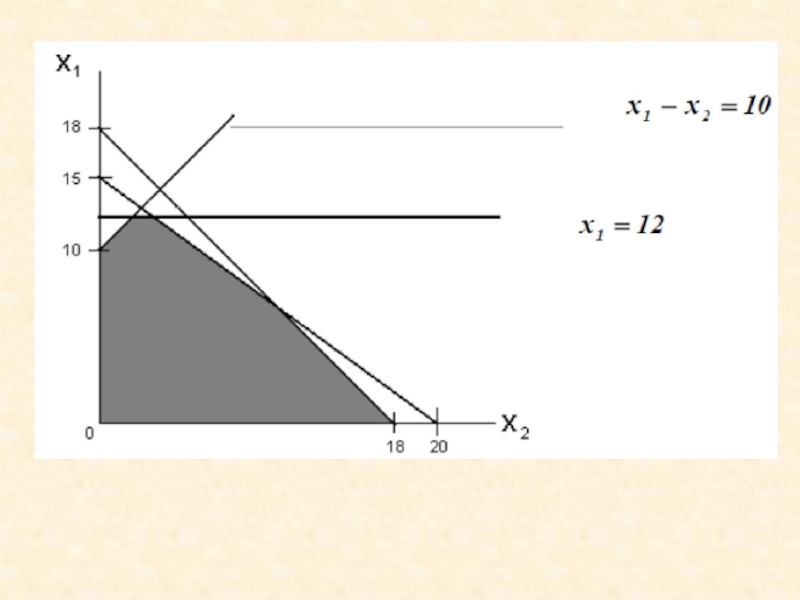
Область допустимых решений представляет собой многоугольник.
Прямая F(x) = const пересекает область в точке D, которая получена в результате пересечения прямых (2) и (3), то ее координаты удовлетворяют уравнениям этих прямых:
2x1+3x2≤18
x1≤2
Решив систему уравнений, получим: x1 = 2, x2 = 4.6667
Откуда найдем максимальное значение целевой функции: F(X) = 4*2 + 3*4.6667 = 22
Слайд 13Оптимальное значение переменной x2=3.5 оказалось нецелочисленным.
Разбиваем задачу
11 на две подзадачи 111 и 112.
В первой из них
к условиям задачи 111 добавляется условие х2 ≥ 4, а к задаче 112 — условие х2 ≤ 3.
Решим графически задачу 111 как задачу ЛП.
3x1+2x2≤16 (1)
2x1+3x2≤18 (2)
x1≥3 (3)
x2≥4 (4)
x1≥0 (5)
x2≥0 (6)
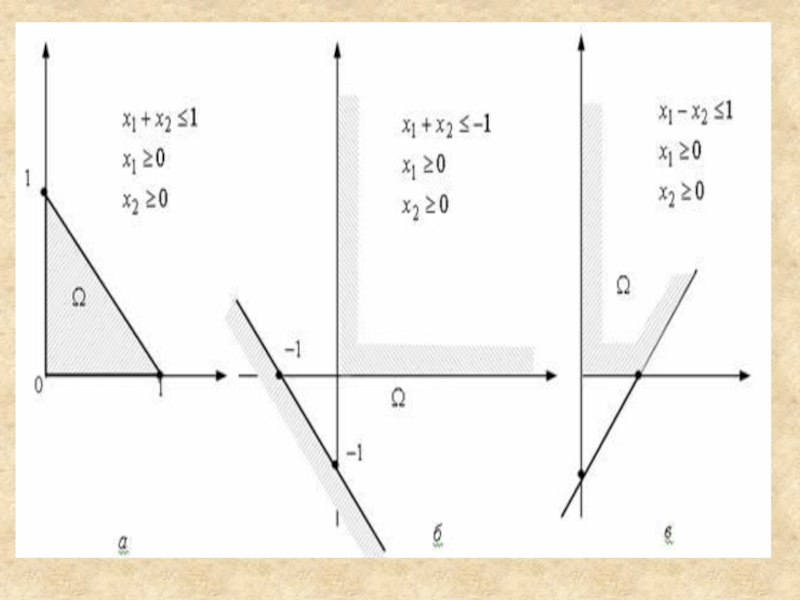
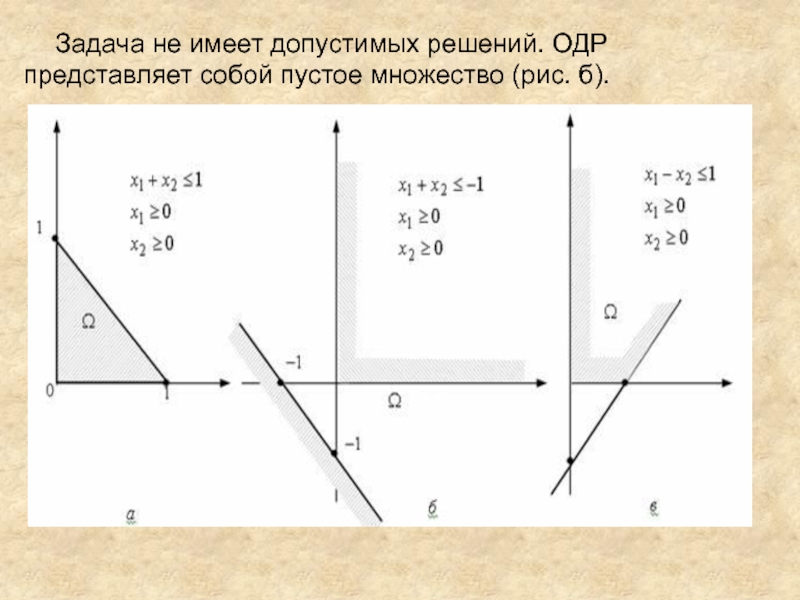
Задача не имеет допустимых решений. ОДР представляет собой пустое множество (рис. б).
Слайд 15Многоугольные области: а - ограниченное множество; б - пустое множество;
в - неограниченное множество
Слайд 16Задача 111 не имеет решения, поэтому для нее процесс ветвления
прерываем.
Решим графически задачу 112 как задачу ЛП
Слайд 17Область допустимых решений представляет собой многоугольник
Прямая F(x) = const пересекает
область в точке C, которая получена в результате пересечения прямых
(1) и (4), ее координаты удовлетворяют уравнениям этих прямых
3x1+2x2≤16
x2≤3
Решив систему уравнений, получим: x1 = 3.3333, x2 = 3
Откуда найдем максимальное значение целевой функции:
F(X) = 4*3.3333 + 3*3 = 22.3333
Слайд 19Оптимальное значение переменной x1=3.33 оказалось нецелочисленным.
Разбиваем задачу 112 на две
подзадачи 1121 и 1122.
В первой из них к условиям задачи
1121 добавляется условие х1 ≥ 4, а к задаче 1122 — условие х1 ≤ 3.
Решим графически задачу 1121 как задачу ЛП.
Слайд 20Область допустимых решений представляет собой треугольник.
Прямая F(x) = const пересекает
область в точке B. Так как точка B получена в
результате пересечения прямых (1) и (5), то ее координаты удовлетворяют уравнениям этих прямых:
3x1+2x2≤16
x1≥4
Решив систему уравнений, получим: x1 = 4, x2 = 2
Откуда найдем максимальное значение целевой функции:
F(X) = 4*4 + 3*2 = 22
Слайд 22Решение задачи получилось целочисленным.
Новое значение текущего рекорда будет равно
F(X)
= 22.
Так как найденная точка является первым целочисленным решением, то
ее и соответствующее ей значение ЦФ следует запомнить.
Сама точка называется текущим целочисленным рекордом или просто рекордом, а оптимальное значение целочисленной задачи — текущим значением рекорда.
Это значение является нижней границей оптимального значения исходной задачи Z*.
Решим графически задачу 1122 как задачу ЛП.
Слайд 23Сведем систему ограничений к следующему виду:
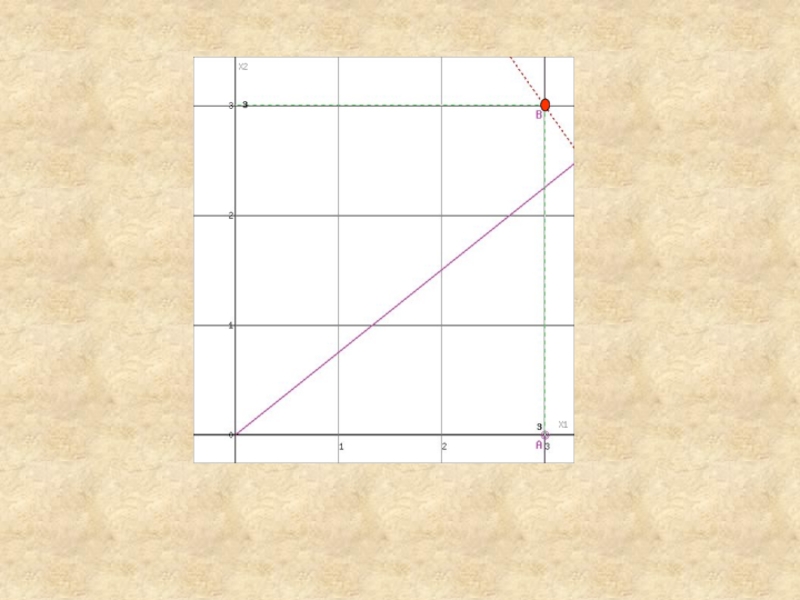
Слайд 24Область допустимых решений представляет собой одну точку.
Прямая F(x) = const
пересекает область в точке B, которая получена в результате пересечения
прямых (3) и (4), то ее координаты удовлетворяют уравнениям этих прямых:
x1=3
x2≤3
Решив систему уравнений, получим: x1 = 3, x2 = 3
Откуда найдем максимальное значение целевой функции:
F(X) = 4*3 + 3*3 = 21
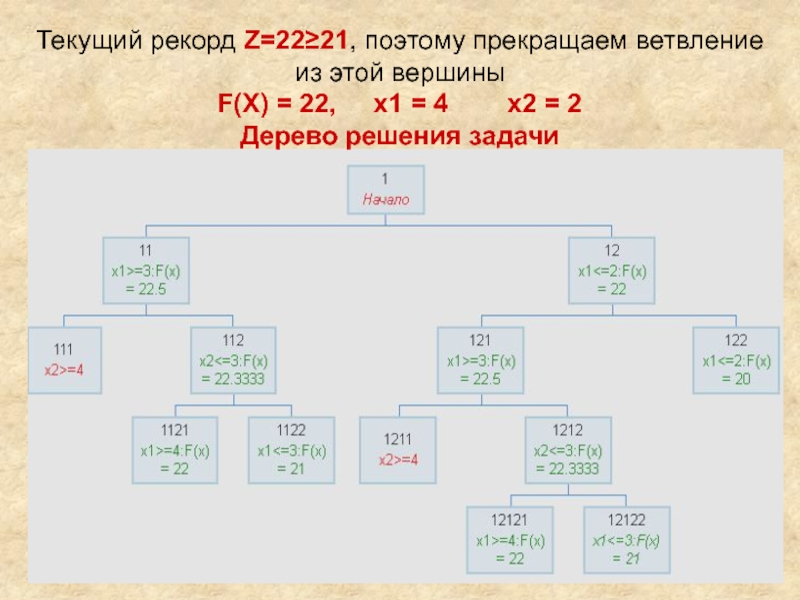
Текущий рекорд Z = 22 ≥ 21, поэтому прекращаем ветвление из этой вершины
Слайд 27
Для первой вершины оптимальное значение переменной x2=4.4 оказалось нецелочисленным.
Разбиваем задачу
1 на две подзадачи 11 и 12.
В первой из них
к условиям задачи 11 добавляется условие х2 ≥ 5, а к задаче 12 — условие х2 ≤ 4.
Эта процедура называется ветвлением по переменной х2.
Слайд 28Решим графически задачу 11 как задачу ЛП.
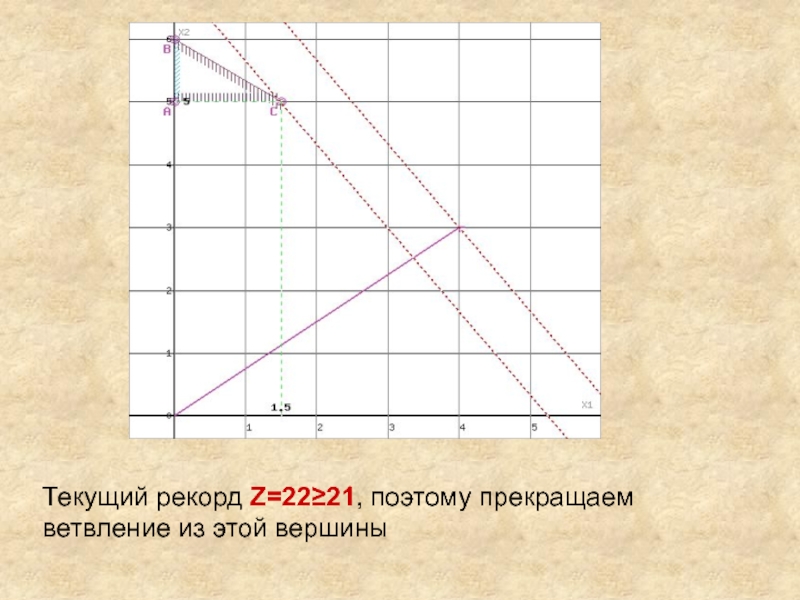
Слайд 29Область допустимых решений представляет собой треугольник.
Прямая F(x) = const пересекает
область в точке C, еоторая получена в результате пересечения прямых
(2) и (3), ее координаты удовлетворяют уравнениям этих прямых:
2x1+3x2≤18
x2≥5
Решив систему уравнений, получим: x1 = 1.5, x2 = 5
Откуда найдем максимальное значение целевой функции:
F(X) = 4*1.5 + 3*5 = 21
Слайд 30Текущий рекорд Z=22≥21, поэтому прекращаем ветвление из этой вершины
Слайд 31
Решим графически задачу 12 как задачу ЛП.
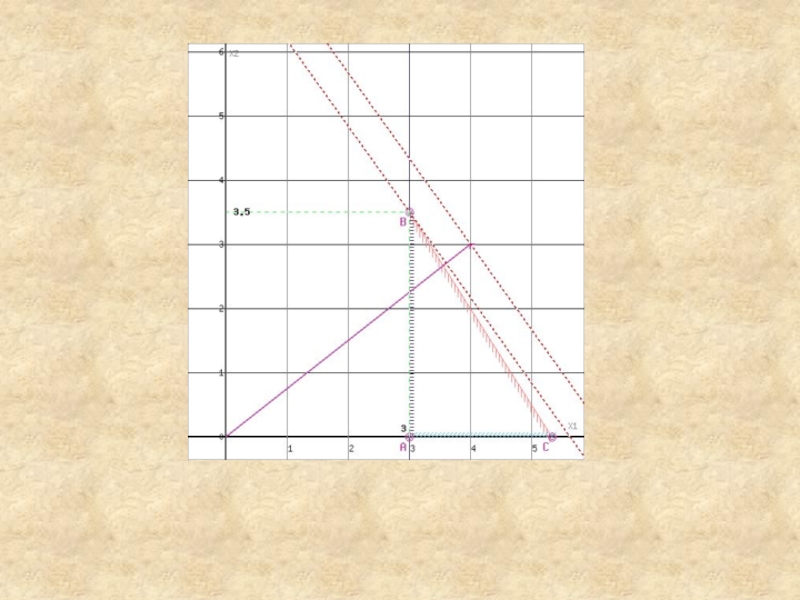
Слайд 32Область допустимых решений представляет собой многоугольник
Прямая F(x) = const пересекает
область в точке C. Так как точка C получена в
результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых:
3x1+2x2≤16
x2≤4
Решив систему уравнений, получим: x1 = 2.6667, x2 = 4
Откуда найдем максимальное значение целевой функции:
F(X) = 4*2.6667 + 3*4 = 22.6667
Слайд 34Оптимальное значение переменной x1=2.67 оказалось нецелочисленным.
Разбиваем задачу 12 на две
подзадачи 121 и 122.
В первой из них к условиям задачи
121 добавляется условие х1 ≥ 3, а к задаче 122 — условие х1 ≤ 2.
Решим графически задачу 121 как задачу ЛП.
Слайд 35Область допустимых решений представляет собой треугольник.
Прямая F(x) = const пересекает
область в точке B. Так как точка B получена в
результате пересечения прямых (1) и (4), то ее координаты удовлетворяют уравнениям этих прямых:
3x1+2x2≤16
x1≥3
Решив систему уравнений, получим: x1 = 3, x2 = 3.5
Откуда найдем максимальное значение целевой функции:
F(X) = 4*3 + 3*3.5 = 22.5
Слайд 37Решим графически задачу 122 как задачу ЛП.
Слайд 38Область допустимых решений представляет собой многоугольник
Прямая F(x) = const пересекает
область в точке D. Так как точка D получена в
результате пересечения прямых (3) и (4), то ее координаты удовлетворяют уравнениям этих прямых:
x2≤4
x1≤2
Решив систему уравнений, получим: x1 = 2, x2 = 4
Откуда найдем максимальное значение целевой функции:
F(X) = 4*2 + 3*4 = 20
Слайд 40Текущий рекорд Z=22≥20, поэтому прекращаем ветвление из этой вершины
Оптимальное значение
переменной x2=3.5 оказалось нецелочисленным.
Разбиваем задачу 121 на две подзадачи 1211
и 1212.
В первой из них к условиям задачи 1211 добавляется условие х2 ≥ 4, а к задаче 1212 — условие х2 ≤ 3.
Слайд 41Решим графически задачу 1211 как задачу ЛП
Сведем систему ограничений
к следующему виду:
Слайд 42Задача не имеет допустимых решений. ОДР представляет собой пустое множество
(рис. б).
Слайд 43Многоугольные области: а - ограниченное множество; б - пустое множество;
в - неограниченное множество
Слайд 44Задача 1211 не имеет решения, поэтому для нее процесс ветвления
прерываем.
Решим графически задачу 1212 как задачу ЛП.
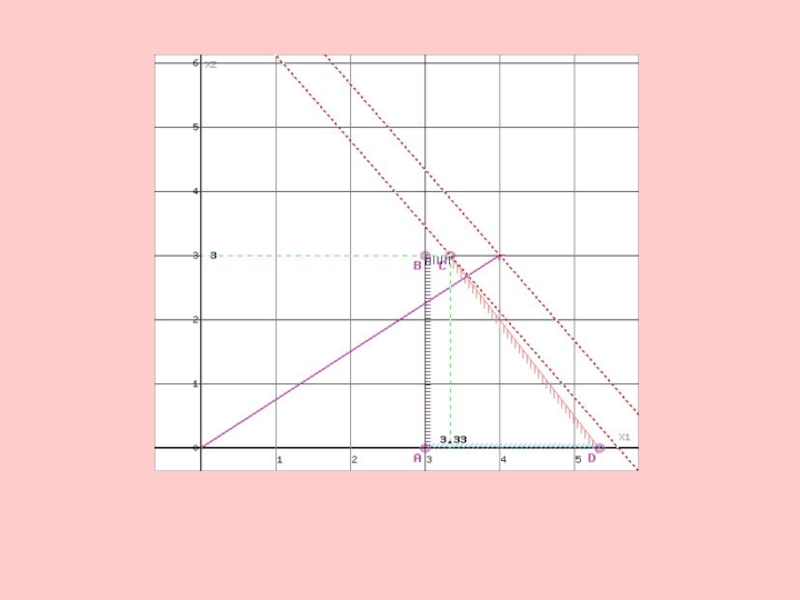
Слайд 45Область допустимых решений представляет собой многоугольник
Прямая F(x) = const пересекает
область в точке C. Так как точка C получена в
результате пересечения прямых (1) и (5), то ее координаты удовлетворяют уравнениям этих прямых:
3x1+2x2≤16
x2≤3
Решив систему уравнений, получим: x1 = 3.3333, x2 = 3
Откуда найдем максимальное значение целевой функции:
F(X) = 4*3.3333 + 3*3 = 22.3333
Слайд 47Оптимальное значение переменной x1=3.33 оказалось нецелочисленным.
Разбиваем задачу 1212 на две
подзадачи 12121 и 12122.
В первой из них к условиям задачи
12121 добавляется условие х1 ≥ 4, а к задаче 12122 — условие х1 ≤ 3.
Решим графически задачу 12121 как задачу ЛП.
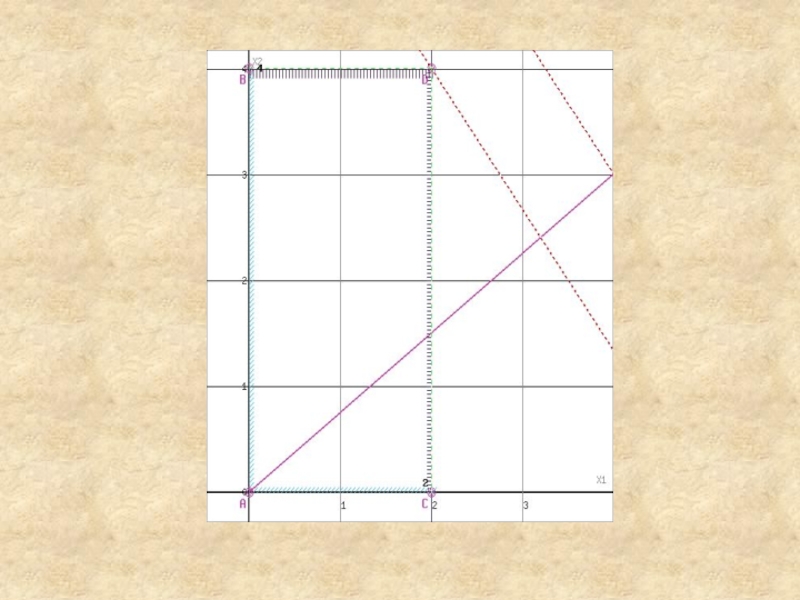
Слайд 48Область допустимых решений представляет собой треугольник.
Прямая F(x) = const пересекает
область в точке B. Так как точка B получена в
результате пересечения прямых (1) и (6), то ее координаты удовлетворяют уравнениям этих прямых:
3x1+2x2≤16
x1≥4
Решив систему уравнений, получим: x1 = 4, x2 = 2
Откуда найдем максимальное значение целевой функции:
F(X) = 4*4 + 3*2 = 22
Слайд 50Текущий рекорд Z=22≥22, поэтому прекращаем ветвление из этой вершины
Решим графически
задачу 12122 как задачу ЛП.
Сведем систему ограничений к следующему виду:
Слайд 51Область допустимых решений представляет собой одну точку.
Прямая F(x) = const
пересекает область в точке B. Так как точка B получена
в результате пересечения прямых (4) и (5), то ее координаты удовлетворяют уравнениям этих прямых:
x1=3
x2≤3
Решив систему уравнений, получим: x1 = 3, x2 = 3
Откуда найдем максимальное значение целевой функции:
F(X) = 4*3 + 3*3 = 21
Слайд 53Текущий рекорд Z=22≥21, поэтому прекращаем ветвление из этой вершины
F(X) =
22, x1 = 4 x2
= 2
Дерево решения задачи
Слайд 63Задача №2 не имеет допустимых значений























































![АВТОМАТИЗАЦИЯ ЗВУКА [ Л ]
В СЛОВАХ](/img/tmb/6/598195/9904114927fd66f267234b3a5c44ea6c-800x.jpg)