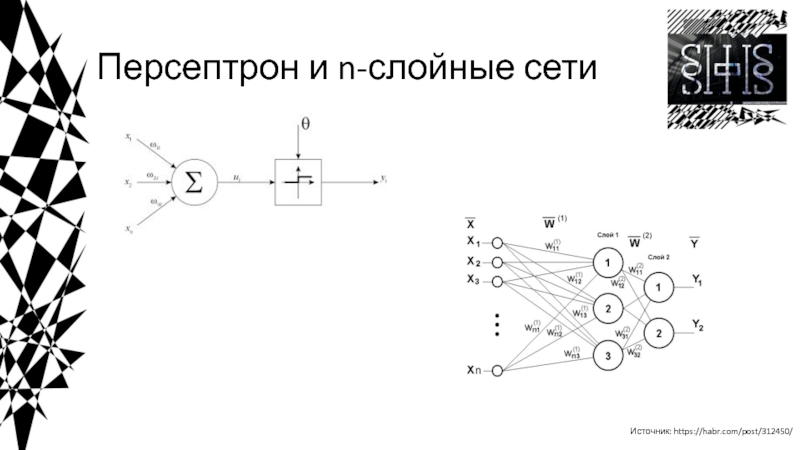
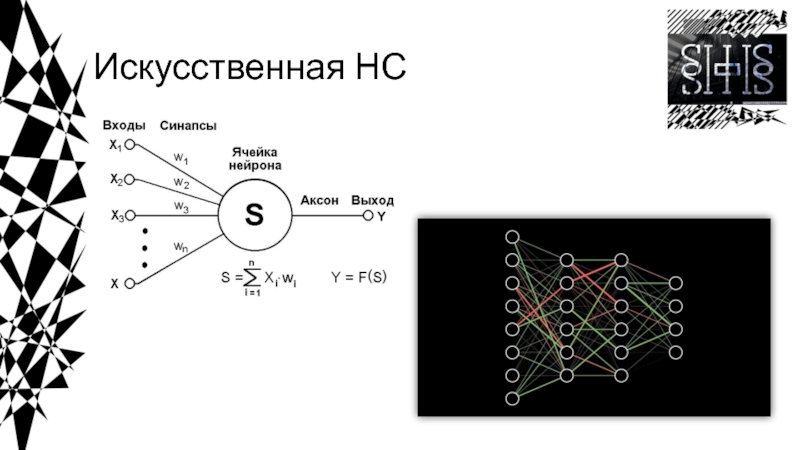
работы, в которых были получены основные результаты в данном направлении,
были проделаны Мак-Каллоком и Питтсом. В 1943 году ими была разработана компьютерная модель нейронной сети на основе математических алгоритмов и теории деятельности головного мозга.Они выдвинули предположение, что нейроны можно упрощённо рассматривать как устройства, оперирующие двоичными числами, и назвали эту модель «пороговой логикой». Подобно своему биологическому прототипу нейроны Мак-Каллока–Питтса были способны обучаться путём подстройки параметров, описывающих синптическую проводимость.
Исследователи предложили конструкцию сети из электронных нейронов и показали, что подобная сеть может выполнять практически любые вообразимые числовые или логические операции. Мак-Каллок и Питтс предположили, что такая сеть в состоянии также обучаться, распознавать образы, обобщать, т. е. обладает всеми чертами интеллекта.
Источник: https://neuronus.com/history/5-istoriya-nejronnykh-setej.html




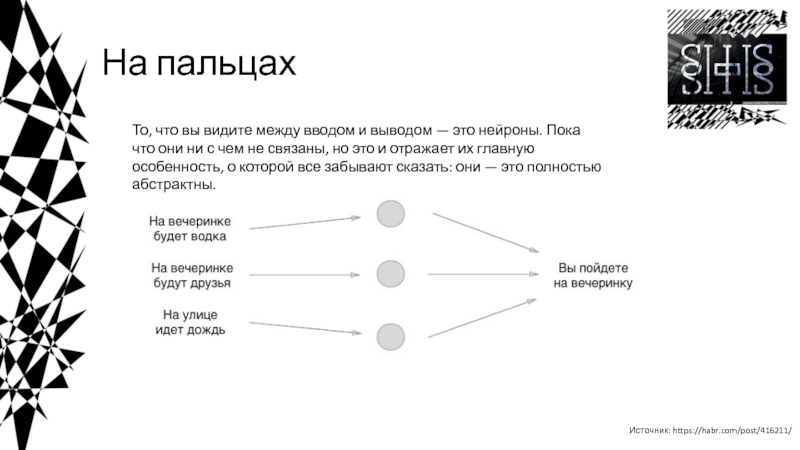
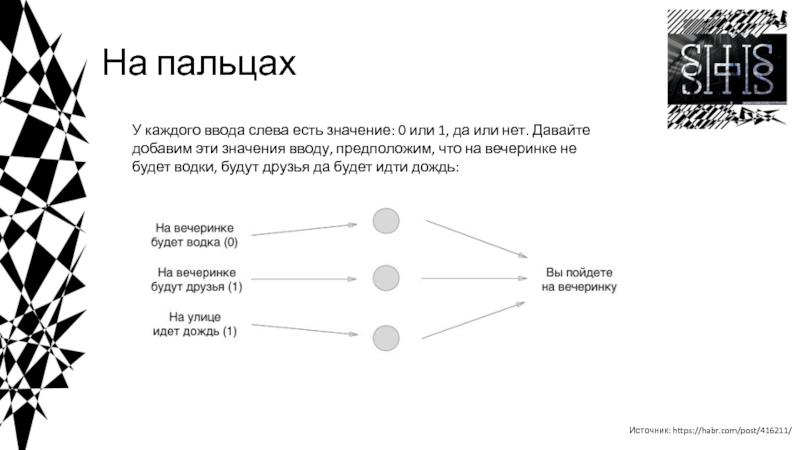
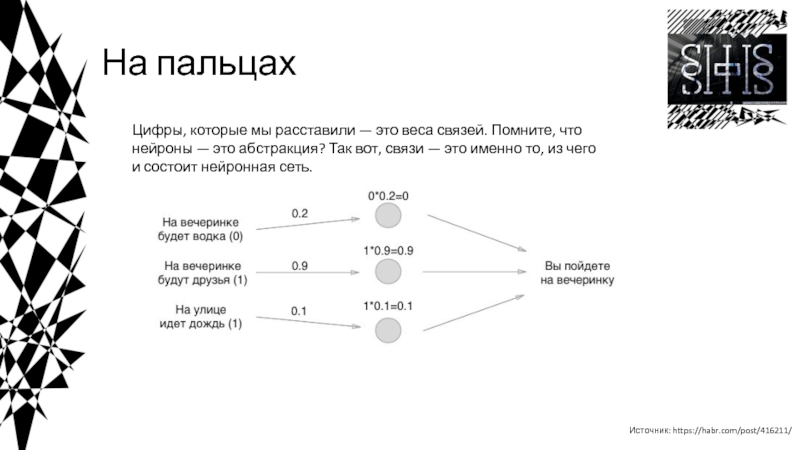
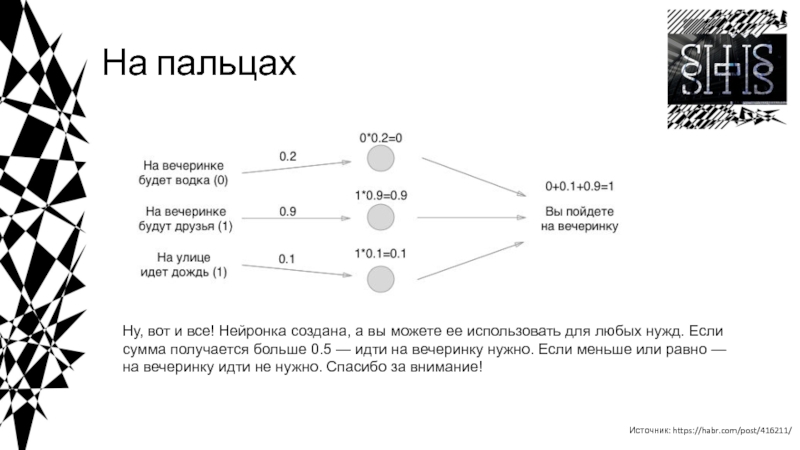
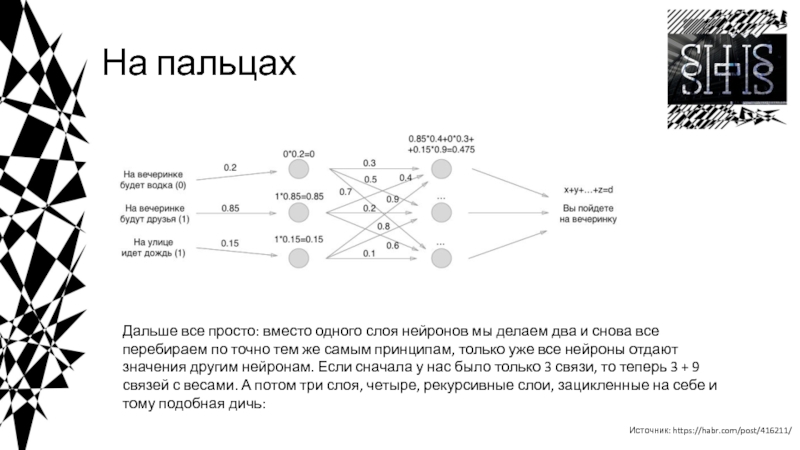
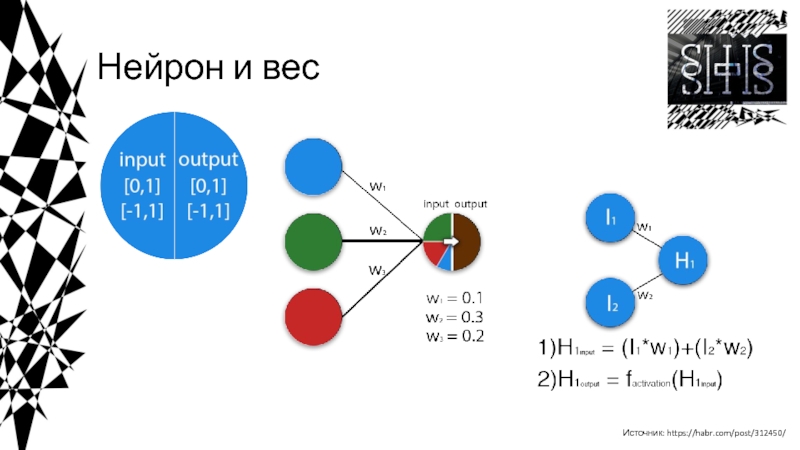










![Введение в нейросети Пример кода на Python*************** epoch 1 ***************weight = [0. 0.]_____________________________________________| net Пример кода на Python*************** epoch 1 ***************weight = [0. 0.]_____________________________________________| net = 0.000 | y](/img/thumbs/0bed973c57a6381a93f17467930a94f4-800x.jpg)