Вычислительная математика

Содержание

1. Вычислительная математика
2. ЛитератураН. С. Бахвалов, Н. П. Жидков, Г.
3. Виды погрешностейПогрешность исходных данных (инструментальная погрешность)Погрешность моделиПогрешность численного методаПогрешность округленияНеустранимыеУстранимые
4. Погрешность
5. Погрешность арифметических операций
6. Погрешность функции
7. Вычисления с плавающей запятой
8. Решение квадратного уравнения
9. Решение квадратного уравнения
10. Обусловленность задачи
11. MATLAB: матричные операторы (операции над матрицами)
12. MATLAB: поэлементные операторы (операции над массивами)
13. Построение графиков в MATLABline(p1,p2) – отрезокplot(x, y
14. Построение графиков в MATLABx=-3:0.1:3;y=x.^2;plot(x, y, '--xr');
15. Построение графиков в MATLABfigure t = 0:pi/20:2*pi; hold on plot(t,sin(t),'-.r*') plot(t,sin(t-pi/2),'--mo') plot(t,sin(t-pi),':bs') hold off plot()
16. Построение графиков в MATLAB[X, Y] = meshgrid(-8:.5:8);R
17. Построение графиков в MATLABtheta = 0:0.01:2*pi;rho = sin(2*theta).*cos(2*theta);figurepolar(theta, rho, '--r') polar()
18. Построение графиков в MATLABt = 0:0.1:1;x = 3*cos(2*pi*t);y = 3*sin(2*pi*t);plot(x, y) параметрическое задание функции
19. Построение графиков в MATLABfiguresubplot(2,2,1)…polar(theta,rho,'--r') subplot(2,2,2)…plot(x,y,'b')subplot(2,2,3)hold onplot(t,sin(t),'-.r*')…hold offsubplot(2,2,4)...mesh(x,y,z)subplot()
20. Программирование в MATLABКомандыsave load Меню «Save Workspace As» «Import Data»Сохранение Workspace
21. Программирование в MATLABСоздание .m файла File>New>ScriptСохранение команд
22. Программирование в MATLABif …elseif …else …endОператор ветвления% проверка дискриминантаif D
23. Программирование в MATLABswitch case … case …otherwise …endОператор выбораswitch operator case ‘+’ y=a+b; case ‘-’ y=a-b; otherwise disp(‘Неизвестный оператор’)end
24. Программирование в MATLABfor v = values …endОператор цикла
25. Программирование в MATLABwhile …endОператор цикла whilen =
26. Программирование в MATLABbreak – выход из циклаcontinue – переход к следующему шагуОператоры изменения хода цикла
27. Программирование в MATLAB===~=Операторы сравнения
28. Программирование в MATLABfunction [y]=f(x) …endФункцииfunction [min_v, max_v]=f(v) min_v=v(1); max_v=v(1); for x=v if min_v > x min_v=x; end if max_v < x max_v=x; end endend
29. Программирование в MATLABУмножение матрицA, Bi=1,nj=1,mk=1,pC(i,j)=0C(i,j)=C(i,j)+A(i,k)*B(k,j)C
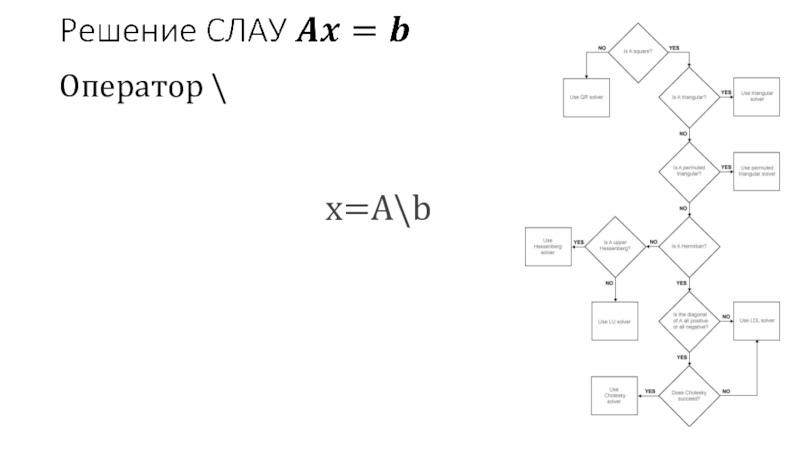
30. Оператор \x=A\b
31. Функция linsolve()x=linsolve(A,b);options.SYM=true;x=linsolve(A,b,options);
32. Метод обратной матрицыx=inv(A)*bx=A^(-1)*b
33. Ai=[A(:,1:i-1), b, A(:,i+1:end)]x(i)=det(Ai)/det(A)D(i)=det(Ai)x=D./det(A)Метод КрамераA, bi=1:numel(b)Ai=[A(:,1:i-1), b, A(:,i+1:end)]x=D./det(A)xD(i)=det(Ai)
34. Число обусловленности матрицыОператорная (подчиненная, индуцированная, согласованная) норма матрицы
35. Число обусловленности матрицы
36. Итерационные методы решения СЛАУМетод простой итерации
37. Итерационные методы решения СЛАУМетод Якоби
38. Итерационные методы решения СЛАУМетод Зейделя (модификация метода
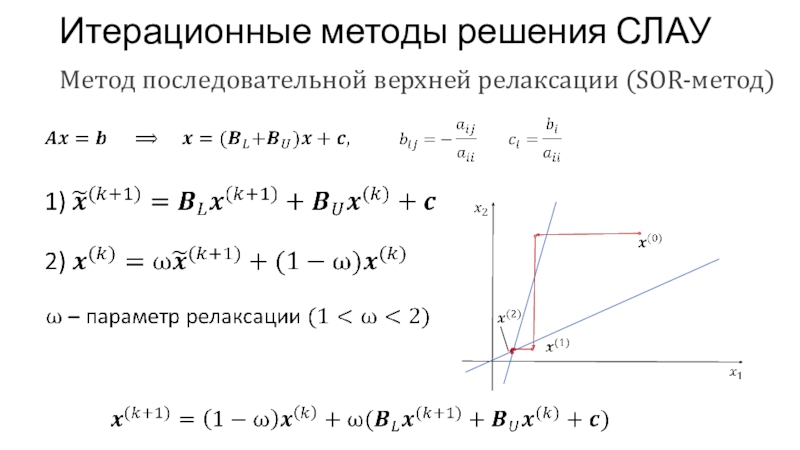
39. Итерационные методы решения СЛАУМетод последовательной верхней релаксации (SOR-метод)
40. Итерационные методы решения СЛАУАлгоритм метода ЯкобиA,b,n,epsjacobim=size(A)B(i,j)=-A(i,j)/A(i,i)j=1:mi=1:mi~=jnb
41. Интерполяционный многочлен ЛагранжаОпределение
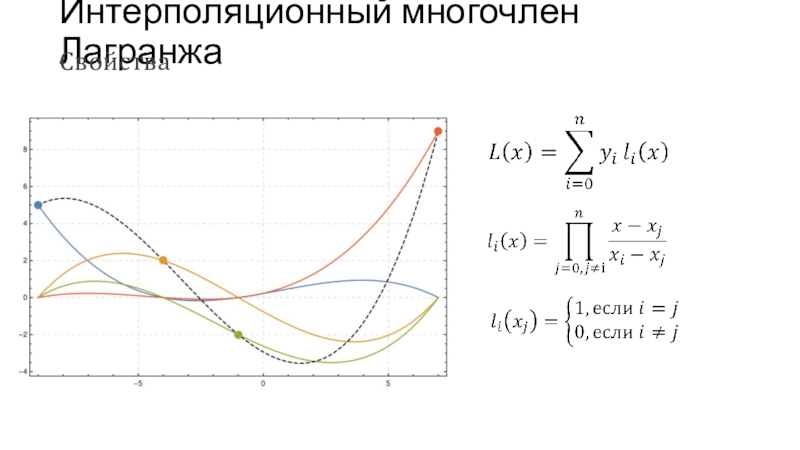
42. Интерполяционный многочлен ЛагранжаСвойства
43. Интерполяционный многочлен ЛагранжаСвойства
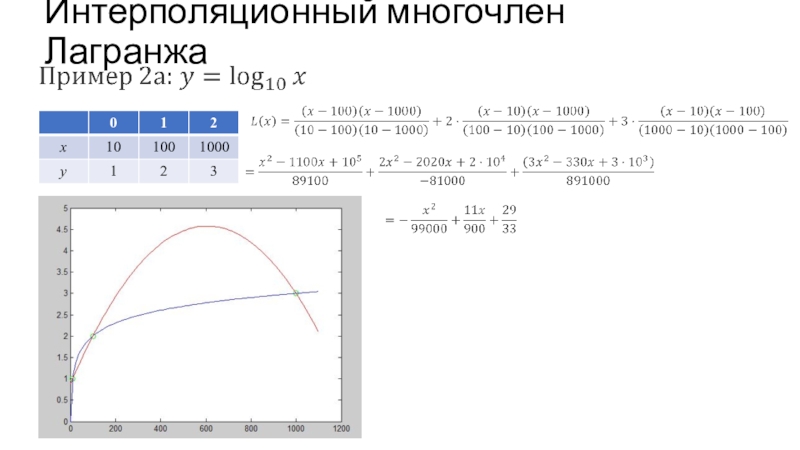
44. Интерполяционный многочлен Лагранжа
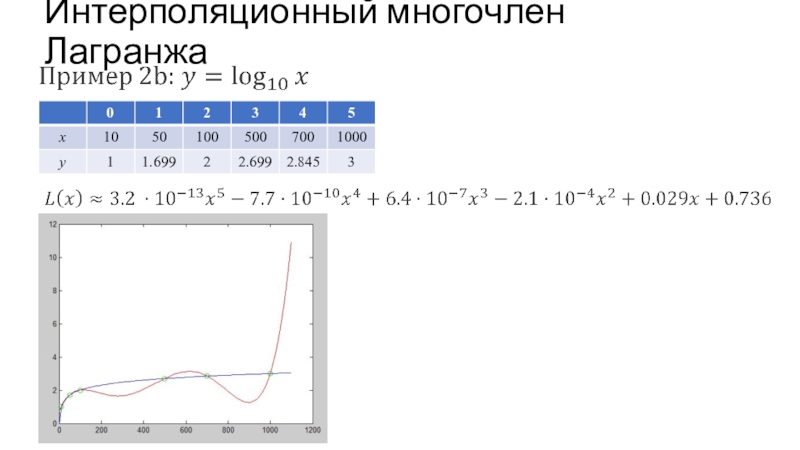
45. Интерполяционный многочлен Лагранжа
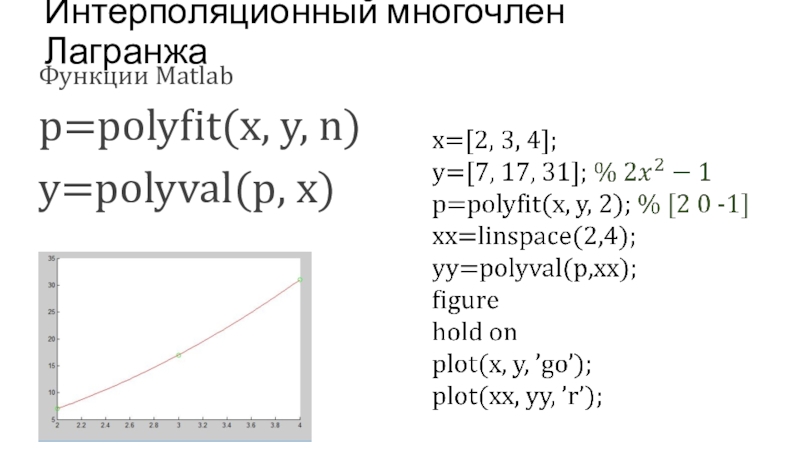
46. Интерполяционный многочлен ЛагранжаФункции Matlabp=polyfit(x, y, n)y=polyval(p, x)
47. x, y, xxlagrangem=length(xx)i=1:mk=1:nyyendИнтерполяционный многочлен ЛагранжаАлгоритм интерполяцииn=length(x)yy=zeros(1,m)l=1j=[1:k-1, k+1:n]
48. Контрольная работа №1Правила выполненияРабота выполняется в Matlab.
49. Численное интегрированиеПостановка задачи
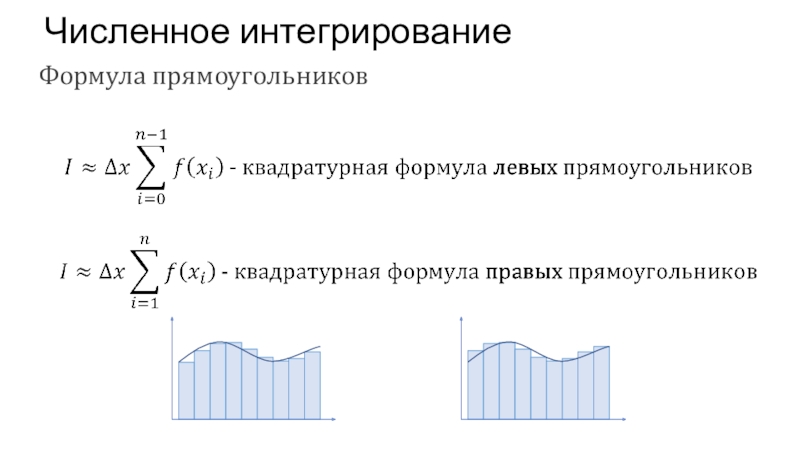
50. Численное интегрированиеФормула прямоугольников
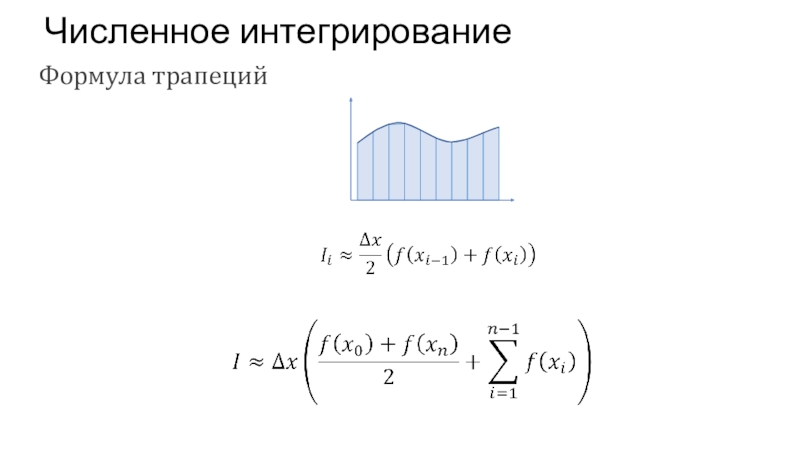
51. Численное интегрированиеФормула трапеций
52. Численное интегрированиеФормула трапеций, MatlabI = trapz(Y)I =
53. Численное интегрированиеФормула Симпсона
54. Численное интегрированиеИнтегрирование многочлена, Matlabq = polyint(p,k) %
55. Символьные вычисления в MatlabСимвольные переменные и функции
56. Численное интегрированиеКвадратурные формулы Гаусса
57. Численное интегрированиеКвадратурные формулы ГауссаКвадратурные формулы Гаусса должны
58. Численное интегрированиеКвадратурные формулы Гауссаfunction y = int_gauss
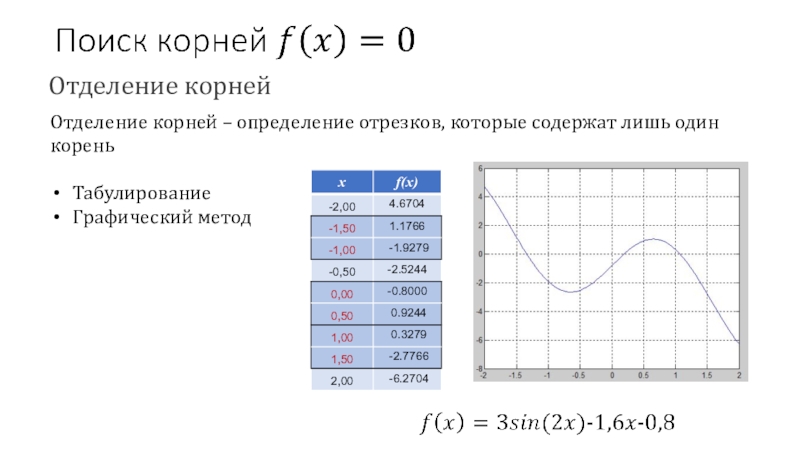
59. Отделение корнейОтделение корней – определение отрезков, которые содержат лишь один кореньТабулированиеГрафический метод
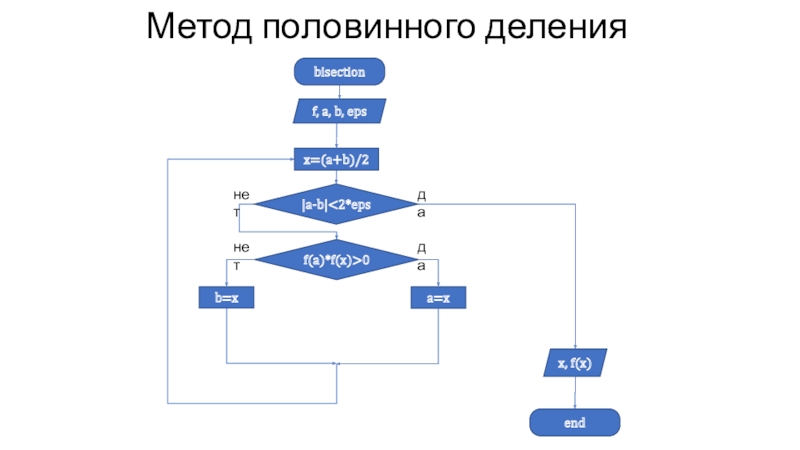
60. Метод половинного деления
61. Метод половинного деленияf, a, b, epsbisectionx, f(x)x=(a+b)/2f(a)*f(x)>0b=xa=x|a-b|
62. Метод простой итерации
63. Слайд 63
64. Слайд 64
65. Метод Ньютона (касательных)
66. Слайд 66
67. Матлаб[x,y]=fzero(f, x0)[x,y]=fzero(f, [a,b])[x,y]=roots(p)
68. АппроксимацияОпределениеАппроксимацией называется приближение, состоящее в замене исходного
69. АппроксимацияМетод наименьших квадратов (МНК, OLS)МНК основан на
70. Функции Matlab для работы с многочленами
71. Решение систем нелинейных уравненийОбобщение метода Ньютона
72. Решение систем нелинейных уравненийMatlab[x, fval, exitflag, output,
73. Задача оптимизации
74. Задача оптимизацииКлассификация
75. Задача оптимизацииМетоды решенияПрямой поиск (одномерная оптимизация)Половинного деленияЗолотого
76. Задача оптимизацииМетод золотого сечения
77. Задача оптимизацииМетод Ньютона
78. Задача оптимизацииМетод наискорейшего спуска (градиентный)
79. Скачать презентанцию

ЛитератураН. С. Бахвалов, Н. П. Жидков, Г. М. Кобельков "Численные методы"https://market.yandex.ru/product--n-s-bakhvalov-n-p-zhidkov-g-m-kobelkov-chislennye-metody/1443487Амосов, Дубинский, Копченова "Вычислительные методы" https://market.yandex.ru/product--amosov-aleksandr-aleksandrovich-dubinskii-iulii-andreevich-kopchenova-natalia-vasilevna-vychislitelnye-metody-uchebnoe-posobie-4-izd/10726410Золотых «Использование пакета Matlab в научной и учебной работе» http://www.uic.unn.ru/~zny/matlab/Book/matlab.sep.pdf

Главная
Разное
Вычислительная математика

Слайды и текст этой презентации

Слайд 1Вычислительная математика
с использованием MATLAB

Слайд 2Литература
Н. С. Бахвалов, Н. П. Жидков, Г. М. Кобельков "Численные

методы"
https://market.yandex.ru/product--n-s-bakhvalov-n-p-zhidkov-g-m-kobelkov-chislennye-metody/1443487
Амосов, Дубинский, Копченова "Вычислительные методы"

https://market.yandex.ru/product--amosov-aleksandr-aleksandrovich-dubinskii-iulii-andreevich-kopchenova-natalia-vasilevna-vychislitelnye-metody-uchebnoe-posobie-4-izd/10726410
Золотых «Использование пакета Matlab в научной

и учебной работе» http://www.uic.unn.ru/~zny/matlab/Book/matlab.sep.pdf

ЛитератураН. С. Бахвалов, Н. П. Жидков, Г. М. Кобельков

Слайд 3Виды погрешностей
Погрешность исходных данных (инструментальная погрешность)
Погрешность модели
Погрешность численного метода
Погрешность округления
Неустранимые
Устранимые

Виды погрешностейПогрешность исходных данных (инструментальная погрешность)Погрешность моделиПогрешность численного методаПогрешность округленияНеустранимыеУстранимые

Слайд 4Погрешность

Слайд 5Погрешность арифметических операций

Слайд 6Погрешность функции

Слайд 7Вычисления с плавающей запятой

Слайд 8Решение квадратного уравнения

Слайд 9Решение квадратного уравнения

Слайд 10Обусловленность задачи

Слайд 11MATLAB: матричные операторы (операции над матрицами)

Слайд 12MATLAB: поэлементные операторы (операции над массивами)

Слайд 13Построение графиков в MATLAB
line(p1,p2) – отрезок
plot(x, y [, linespec]) –

2D график
plot3(x, y, z [, linespec]) – 3D график
comet(x, y

[, p]) – анимированный 2D график
comet3(x, y, z [, p]) – анимированный 3D график
polar(theta, ro [, linespec]) – график в полярных координатах
mesh(x, y, z [, color]) – сетка
surf(x, y, z [, color]) – поверхность (закрашенная сетка)

Построение графиков в MATLABline(p1,p2) – отрезокplot(x, y [, linespec]) – 2D графикplot3(x, y, z [, linespec]) –

Слайд 14Построение графиков в MATLAB
x=-3:0.1:3;
y=x.^2;
plot(x, y, '--xr');

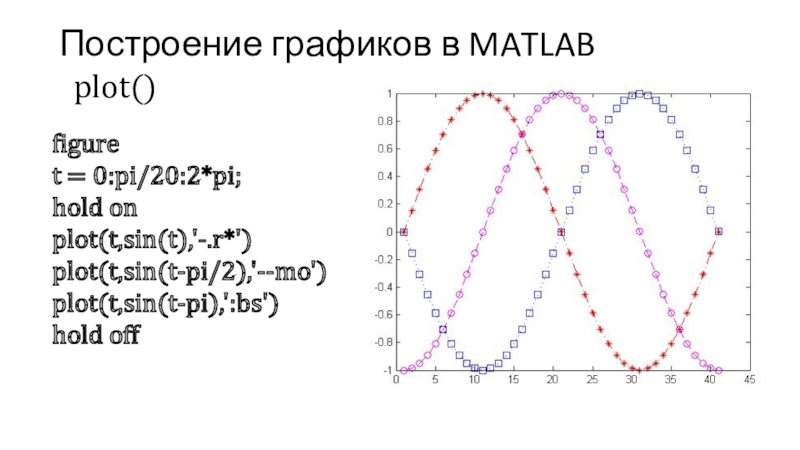
Слайд 15Построение графиков в MATLAB
figure
t = 0:pi/20:2pi;
hold on
plot(t,sin(t),'-.r')

plot(t,sin(t-pi/2),'--mo')
plot(t,sin(t-pi),':bs')
hold off

plot()

Слайд 16Построение графиков в MATLAB
[X, Y] = meshgrid(-8:.5:8);
R = sqrt(X.^2 +

Y.^2);
Z = sin(R)./R;
C = gradient(Z);
figure
mesh(X, Y, Z, C)
mesh()

Построение графиков в MATLAB[X, Y] = meshgrid(-8:.5:8);R = sqrt(X.^2 + Y.^2);Z = sin(R)./R;C = gradient(Z);figuremesh(X, Y, Z,

Слайд 17Построение графиков в MATLAB
theta = 0:0.01:2pi;
rho = sin(2theta).cos(2theta);
figure
polar(theta, rho, '--r')

polar()

Слайд 18Построение графиков в MATLAB
t = 0:0.1:1;
x = 3cos(2pit);
y = 3sin(2pit);
plot(x,

y)
параметрическое задание функции

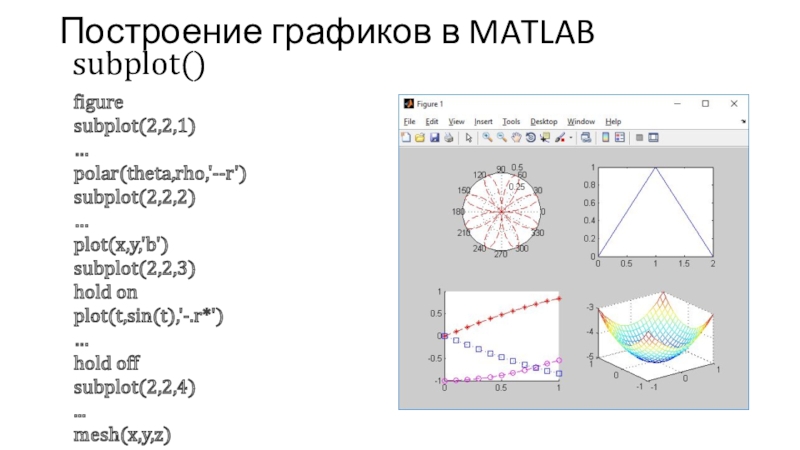
Слайд 19Построение графиков в MATLAB
figure
subplot(2,2,1)
…
polar(theta,rho,'--r')
subplot(2,2,2)
…
plot(x,y,'b')
subplot(2,2,3)
hold on
plot(t,sin(t),'-.r*')
…
hold off
subplot(2,2,4)
...
mesh(x,y,z)
subplot()

Построение графиков в MATLABfiguresubplot(2,2,1)…polar(theta,rho,'--r') subplot(2,2,2)…plot(x,y,'b')subplot(2,2,3)hold onplot(t,sin(t),'-.r*')…hold offsubplot(2,2,4)...mesh(x,y,z)subplot()

Слайд 20Программирование в MATLAB
Команды
save

load

Меню
«Save Workspace As»
«Import

Data»

Сохранение Workspace

Слайд 21Программирование в MATLAB
Создание .m файла
File>New>Script
Сохранение команд

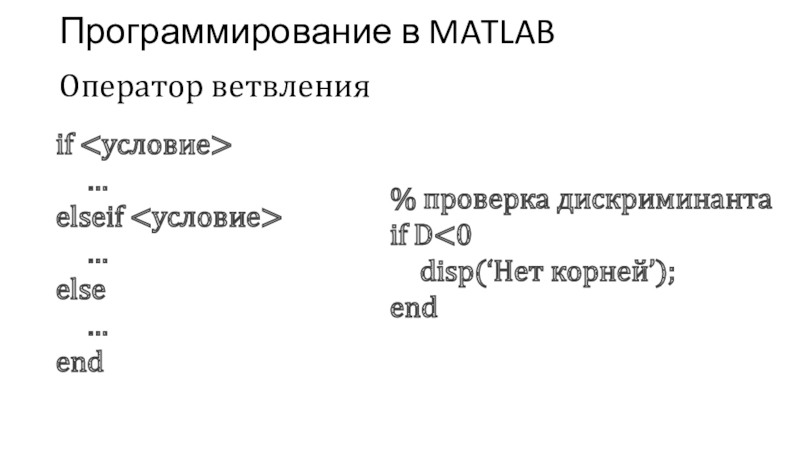
Слайд 22Программирование в MATLAB
if
…
elseif
…
else
…
end
Оператор ветвления
% проверка дискриминанта
if D

Слайд 23Программирование в MATLAB
switch
case
…
case
…
otherwise
…
end
Оператор выбора
switch operator
case ‘+’
y=a+b;
case ‘-’

y=a-b;
otherwise
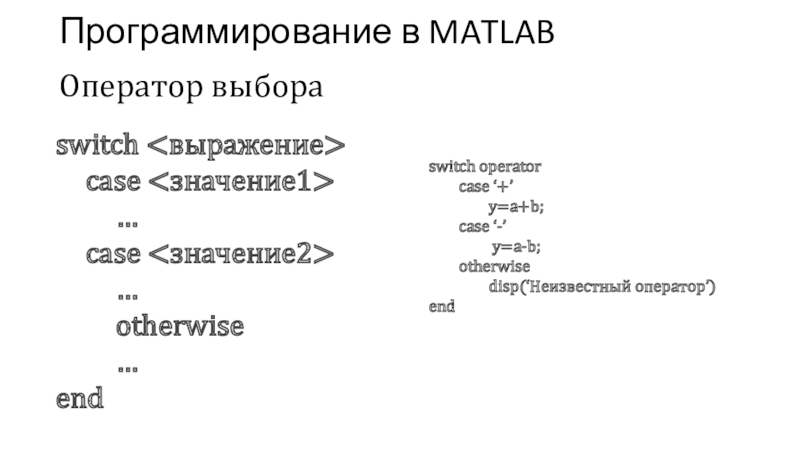
disp(‘Неизвестный оператор’)
end

Программирование в MATLABswitch case … case …otherwise …endОператор выбораswitch operator case ‘+’ y=a+b; case ‘-’ y=a-b; otherwise disp(‘Неизвестный оператор’)end

Слайд 24Программирование в MATLAB
for v = values
…
end
Оператор цикла for
x = [4

5 6];
s=0
for i=1:length(x)
s = s + x(i)
end
% или
for v=x
s

= s + v
end

Программирование в MATLABfor v = values …endОператор цикла forx = [4 5 6];s=0for i=1:length(x) s = s + x(i)end

Слайд 25Программирование в MATLAB
while
…
end
Оператор цикла while
n = 10;
f =

n;
while n > 1
n = n-1;
f

= f*n;
end
disp(['n! = ' num2str(f)])

Программирование в MATLABwhile …endОператор цикла whilen = 10;f = n;while n > 1 n = n-1;

Слайд 26Программирование в MATLAB
break – выход из цикла

continue – переход к

следующему шагу
Операторы изменения хода цикла

Слайд 27Программирование в MATLAB

=
==
~=
Операторы сравнения

Слайд 28Программирование в MATLAB
function [y]=f(x)
…
end
Функции
function [min_v, max_v]=f(v)
min_v=v(1);
max_v=v(1);
for x=v
if min_v > x
min_v=x;
end

if max_v < x
max_v=x;
end
end
end

Слайд 29Программирование в MATLAB
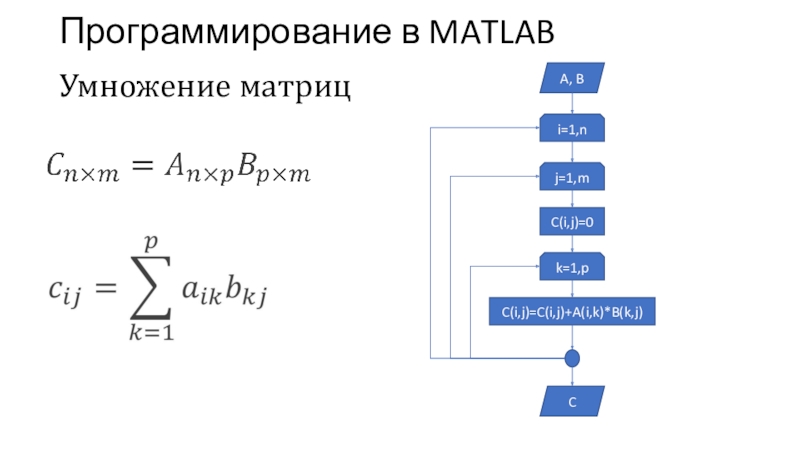
Умножение матриц
A, B
i=1,n
j=1,m
k=1,p
C(i,j)=0
C(i,j)=C(i,j)+A(i,k)*B(k,j)
C

Слайд 30Оператор \
x=A\b

$Оператор \x=A\b$

Слайд 31Функция linsolve()
x=linsolve(A,b);
options.SYM=true;
x=linsolve(A,b,options);

Слайд 32Метод обратной матрицы
x=inv(A)b
x=A^(-1)b

Слайд 33Ai=[A(:,1:i-1), b, A(:,i+1:end)]
x(i)=det(Ai)/det(A)

D(i)=det(Ai)
x=D./det(A)
Метод Крамера
A, b
i=1:numel(b)
Ai=[A(:,1:i-1), b, A(:,i+1:end)]
x=D./det(A)
x
D(i)=det(Ai)

Слайд 34Число обусловленности матрицы
Операторная (подчиненная, индуцированная, согласованная) норма матрицы

Слайд 35Число обусловленности матрицы

Слайд 36Итерационные методы решения СЛАУ
Метод простой итерации

Слайд 37Итерационные методы решения СЛАУ
Метод Якоби

Слайд 38Итерационные методы решения СЛАУ
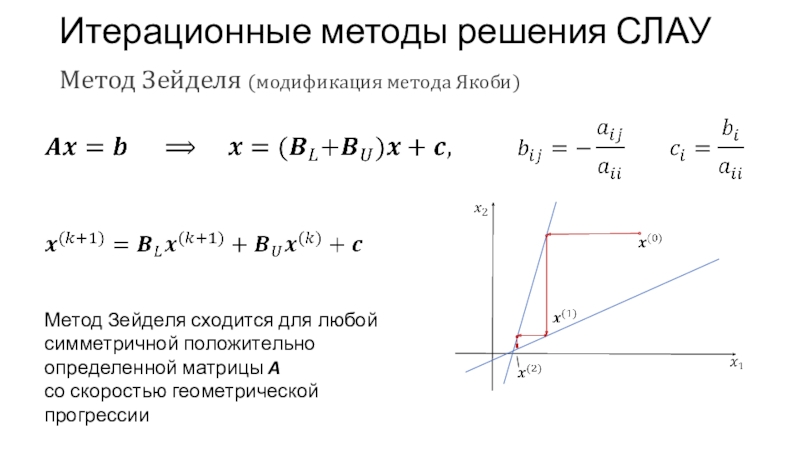
Метод Зейделя (модификация метода Якоби)
Метод Зейделя сходится

для любой симметричной положительно определенной матрицы A
со скоростью геометрической прогрессии

Итерационные методы решения СЛАУМетод Зейделя (модификация метода Якоби)Метод Зейделя сходится для любой симметричной положительно определенной матрицы Aсо

Слайд 39Итерационные методы решения СЛАУ
Метод последовательной верхней релаксации (SOR-метод)

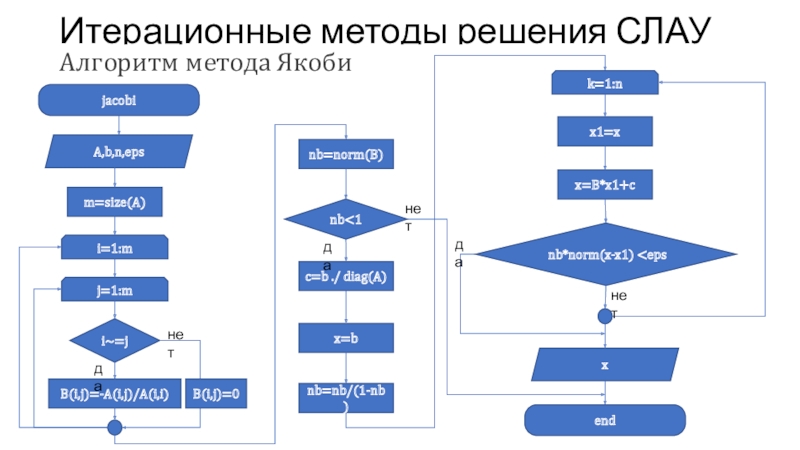
Слайд 40Итерационные методы решения СЛАУ
Алгоритм метода Якоби
A,b,n,eps
jacobi
m=size(A)
B(i,j)=-A(i,j)/A(i,i)
j=1:m
i=1:m
i~=j
nb

Слайд 41Интерполяционный многочлен Лагранжа
Определение

Слайд 42Интерполяционный многочлен Лагранжа
Свойства

Слайд 43Интерполяционный многочлен Лагранжа
Свойства

Слайд 44Интерполяционный многочлен Лагранжа

Слайд 45Интерполяционный многочлен Лагранжа

Слайд 46Интерполяционный многочлен Лагранжа
Функции Matlab
p=polyfit(x, y, n)
y=polyval(p, x)

Слайд 47x, y, xx
lagrange
m=length(xx)
i=1:m
k=1:n
yy
end
Интерполяционный многочлен Лагранжа
Алгоритм интерполяции
n=length(x)
yy=zeros(1,m)
l=1
j=[1:k-1, k+1:n]

Слайд 48Контрольная работа №1
Правила выполнения
Работа выполняется в Matlab. Решение предоставляется в

виде основного .m файла и .m файлов с использованными функциями

Решение

СЛАУ методами Гаусса или Якоби: показать промежуточные вычисления или использовать свою функцию gauss() или jacobi()

Для построения графика результата интерполяции использовать свою функцию lagrange(). На графике показать узлы интерполяции (звездочки или окружности)

Контрольная работа №1Правила выполненияРабота выполняется в Matlab. Решение предоставляется в виде основного .m файла и .m файлов

Слайд 49Численное интегрирование
Постановка задачи

Слайд 50Численное интегрирование
Формула прямоугольников

Слайд 51Численное интегрирование
Формула трапеций

Слайд 52Численное интегрирование
Формула трапеций, Matlab
I = trapz(Y)
I = dx*trapz(Y)
I = trapz(X,Y)
I

= trapz(X,Y,dim)

x = -3:0.1:3;
y = -5:0.1:5;
[X,Y] = meshgrid(x,y);
F=X.^2+Y.^2;
I =

trapz(y, trapz(x,F,2));

Численное интегрированиеФормула трапеций, MatlabI = trapz(Y)I = dx*trapz(Y)I = trapz(X,Y)I = trapz(X,Y,dim)x = -3:0.1:3;y = -5:0.1:5;[X,Y] =

Слайд 53Численное интегрирование
Формула Симпсона

Слайд 54Численное интегрирование
Интегрирование многочлена, Matlab
q = polyint(p,k) % вычислить коэффициенты полинома

интеграла

% с константой интегрирования k

I = diff(polyval(q, [a,b])); % F(b) – F(a)

p = [3 -5 0 4];
q = polyint(p); % q=[0.75 -1.67 0 4 0]
I = diff(polyval(q, [-3, 5])); % I=186.67

Численное интегрированиеИнтегрирование многочлена, Matlabq = polyint(p,k) % вычислить коэффициенты полинома интеграла

Слайд 55Символьные вычисления в Matlab
Символьные переменные и функции

Слайд 56Численное интегрирование
Квадратурные формулы Гаусса

Слайд 57Численное интегрирование
Квадратурные формулы Гаусса
Квадратурные формулы Гаусса должны быть точны для

функций f(t)=1,t ,t2 … tm
При m=2N+1 система имеет единственное решение:

Численное интегрированиеКвадратурные формулы ГауссаКвадратурные формулы Гаусса должны быть точны для функций f(t)=1,t ,t2 … tmПри m=2N+1 система

Слайд 58Численное интегрирование
Квадратурные формулы Гаусса
function y = int_gauss (f, A, B,

n)
% f – функция
%

A, B – пределы интегрирования
% n – число узлов интерполяции
a= […];
t = […];

x = 0.5*(A*(1-t(:,n))+B*(1+t(:,n)));
F=a(:,n).*f(x);
y=0.5*(B-A)*sum(F);

end

Слайд 59Отделение корней
Отделение корней – определение отрезков, которые содержат лишь один

корень

Табулирование
Графический метод

Слайд 60Метод половинного деления

Слайд 61Метод половинного деления
f, a, b, eps
bisection
x, f(x)
x=(a+b)/2
f(a)*f(x)>0
b=x
a=x
|a-b|

Слайд 62Метод простой итерации

Слайд 63

Слайд 64

Слайд 65Метод Ньютона (касательных)

Слайд 66

Слайд 67Матлаб
[x,y]=fzero(f, x0)
[x,y]=fzero(f, [a,b])
[x,y]=roots(p)

Слайд 68Аппроксимация
Определение
Аппроксимацией называется приближение, состоящее в замене исходного объекта более простым,

но близким к исходному.
Примеры
Формулы прямоугольников, трапеций и т.д. для вычисления

интеграла
Замена функции (заданной как аналитически, так и набором точек) другой функцией, например полиномом (первыми членами ряда Тейлора)

АппроксимацияОпределениеАппроксимацией называется приближение, состоящее в замене исходного объекта более простым, но близким к исходному.ПримерыФормулы прямоугольников, трапеций и

Слайд 69Аппроксимация
Метод наименьших квадратов (МНК, OLS)
МНК основан на минимизации суммы квадратов

отклонений.
МНК применяется для решения различных задач: решение переопределенных систем уравнений,

поиск решения нелинейных уравнений, аппроксимации, регрессионного анализа.

В случае аппроксимации полиномиальной функцией метод сводится к поиску коэффициентов многочлена

АппроксимацияМетод наименьших квадратов (МНК, OLS)МНК основан на минимизации суммы квадратов отклонений.МНК применяется для решения различных задач: решение

Слайд 70Функции Matlab для работы с многочленами

Слайд 71Решение систем нелинейных уравнений
Обобщение метода Ньютона

Слайд 72Решение систем нелинейных уравнений
Matlab
[x, fval, exitflag, output, jacobian] = fsolve

(fun, x0, options, P1, P2…)
x – корень
fval – fun(x)
exitflag –

>0 – решение сходится, <0 – не сходится, 0 – превышено число итераций
output – структура с параметрами оптимизации
jacobian – якобиан fun

fun - функция
x0 – начальное приближение
options – параметры оптимизации (TolFun, TolX, MaxIter и др.)
P1, P2 и т.д. – дополнительные параметры функции: fun(x,P1,P2…) –

Решение систем нелинейных уравненийMatlab[x, fval, exitflag, output, jacobian] = fsolve (fun, x0, options, P1, P2…)x – кореньfval

Слайд 73Задача оптимизации

Слайд 74Задача оптимизации
Классификация

Слайд 75Задача оптимизации
Методы решения
Прямой поиск (одномерная оптимизация)
Половинного деления
Золотого сечения

Покоординатный спуск (напр.

метод Зейделя)

Градиентные
Наискорейшего спуска
Сопряженных градиентов

На основе метода Ньютона
Ньютона-Рафсона
Квази-ньютоновские

Дискретные
Симплекс-метод

Задача оптимизацииМетоды решенияПрямой поиск (одномерная оптимизация)Половинного деленияЗолотого сеченияПокоординатный спуск (напр. метод Зейделя)ГрадиентныеНаискорейшего спускаСопряженных градиентовНа основе метода НьютонаНьютона-РафсонаКвази-ньютоновскиеДискретныеСимплекс-метод

Слайд 76Задача оптимизации
Метод золотого сечения

Слайд 77Задача оптимизации
Метод Ньютона

Слайд 78Задача оптимизации
Метод наискорейшего спуска (градиентный)

Скачать презентацию

Разделы презентаций

Вычислительная математика

Содержание

Слайды и текст этой презентации

Слайд 1Вычислительная математикас использованием MATLAB

Слайд 2ЛитератураН. С. Бахвалов, Н. П. Жидков, Г. М. Кобельков "Численные

Слайд 4Погрешность

Слайд 5Погрешность арифметических операций

Слайд 6Погрешность функции

Слайд 7Вычисления с плавающей запятой

Слайд 8Решение квадратного уравнения

Слайд 9Решение квадратного уравнения

Слайд 10Обусловленность задачи

Слайд 11MATLAB: матричные операторы (операции над матрицами)

Слайд 12MATLAB: поэлементные операторы (операции над массивами)

Слайд 13Построение графиков в MATLABline(p1,p2) – отрезокplot(x, y [, linespec]) –

2D графикplot3(x, y, z [, linespec]) – 3D графикcomet(x, y

Слайд 14Построение графиков в MATLABx=-3:0.1:3;y=x.^2;plot(x, y, '--xr');

Слайд 15Построение графиков в MATLABfigure t = 0:pi/20:2*pi; hold on plot(t,sin(t),'-.r*')

plot(t,sin(t-pi/2),'--mo') plot(t,sin(t-pi),':bs') hold off plot()

Слайд 16Построение графиков в MATLAB[X, Y] = meshgrid(-8:.5:8);R = sqrt(X.^2 +

Y.^2);Z = sin(R)./R;C = gradient(Z);figuremesh(X, Y, Z, C) mesh()

Слайд 17Построение графиков в MATLABtheta = 0:0.01:2*pi;rho = sin(2*theta).*cos(2*theta);figurepolar(theta, rho, '--r')

polar()

Слайд 18Построение графиков в MATLABt = 0:0.1:1;x = 3*cos(2*pi*t);y = 3*sin(2*pi*t);plot(x,

y) параметрическое задание функции

Слайд 19Построение графиков в MATLABfiguresubplot(2,2,1)…polar(theta,rho,'--r') subplot(2,2,2)…plot(x,y,'b')subplot(2,2,3)hold onplot(t,sin(t),'-.r*')…hold offsubplot(2,2,4)...mesh(x,y,z)subplot()

Слайд 20Программирование в MATLABКомандыsave load Меню «Save Workspace As» «Import

Data»Сохранение Workspace

Слайд 21Программирование в MATLABСоздание .m файла File>New>ScriptСохранение команд

Слайд 22Программирование в MATLABif …elseif …else …endОператор ветвления% проверка дискриминантаif D

Слайд 23Программирование в MATLABswitch case … case …otherwise …endОператор выбораswitch operator case ‘+’ y=a+b; case ‘-’

y=a-b; otherwise disp(‘Неизвестный оператор’)end

Слайд 24Программирование в MATLABfor v = values …endОператор цикла forx = [4

5 6];s=0for i=1:length(x) s = s + x(i)end % илиfor v=x s

Слайд 25Программирование в MATLABwhile …endОператор цикла whilen = 10;f =

n;while n > 1 n = n-1; f

Слайд 26Программирование в MATLABbreak – выход из циклаcontinue – переход к

следующему шагуОператоры изменения хода цикла

Слайд 27Программирование в MATLAB===~=Операторы сравнения

Слайд 28Программирование в MATLABfunction [y]=f(x) …endФункцииfunction [min_v, max_v]=f(v) min_v=v(1); max_v=v(1); for x=v if min_v > x min_v=x; end

if max_v < x max_v=x; end endend

Слайд 29Программирование в MATLABУмножение матрицA, Bi=1,nj=1,mk=1,pC(i,j)=0C(i,j)=C(i,j)+A(i,k)*B(k,j)C

Слайд 30Оператор \x=A\b

Слайд 31Функция linsolve()x=linsolve(A,b);options.SYM=true;x=linsolve(A,b,options);

Слайд 32Метод обратной матрицыx=inv(A)*bx=A^(-1)*b

Слайд 33Ai=[A(:,1:i-1), b, A(:,i+1:end)]x(i)=det(Ai)/det(A)D(i)=det(Ai)x=D./det(A)Метод КрамераA, bi=1:numel(b)Ai=[A(:,1:i-1), b, A(:,i+1:end)]x=D./det(A)xD(i)=det(Ai)

Слайд 34Число обусловленности матрицыОператорная (подчиненная, индуцированная, согласованная) норма матрицы