Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выполнила Алина Романовна Кустова студентка гр. ТЭМ-58 Научный
Содержание
- 1. Выполнила Алина Романовна Кустова студентка гр. ТЭМ-58 Научный
- 2. «Есть в математике нечто, вызывающее человеческий восторг»
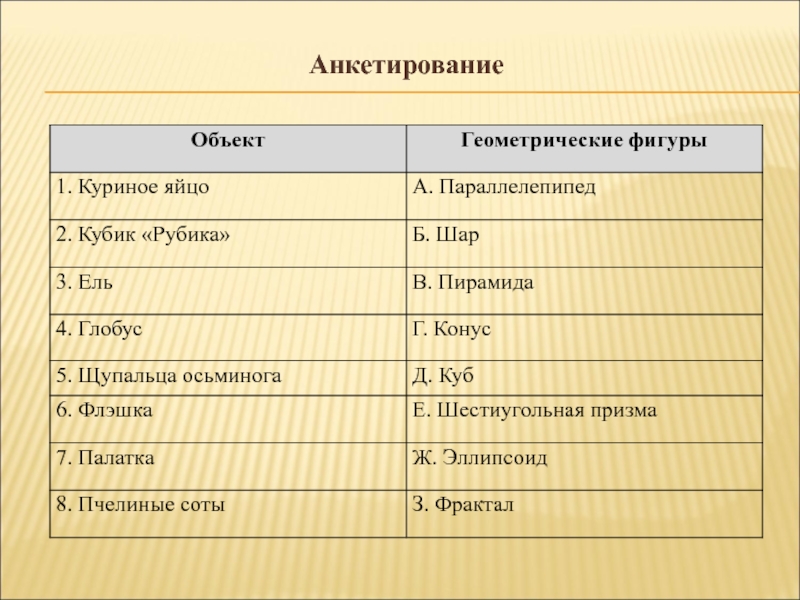
- 3. Анкетирование
- 4. Результаты анкетированияКоличество студентов, верно установивших соответствие между объектом и его геометрической формой
- 5. Актуальность исследования обусловлена противоречием между масштабным распространением
- 6. Объект: Человек, математические абстракции, созданные человеком, изобретения человека,
- 7. Бенуа Мандельброт (1924-2010)Теоретические основы фрактальной геометрии Фрактал (от латинского
- 8. Теоретические основы фрактальной геометрии Фрактал характеризуется следующими особенностями:обладает
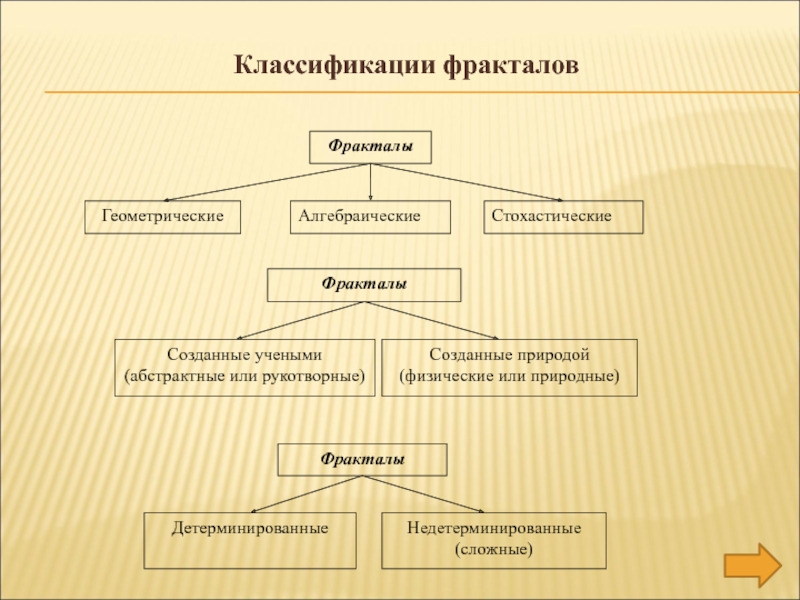
- 9. Классификации фракталов
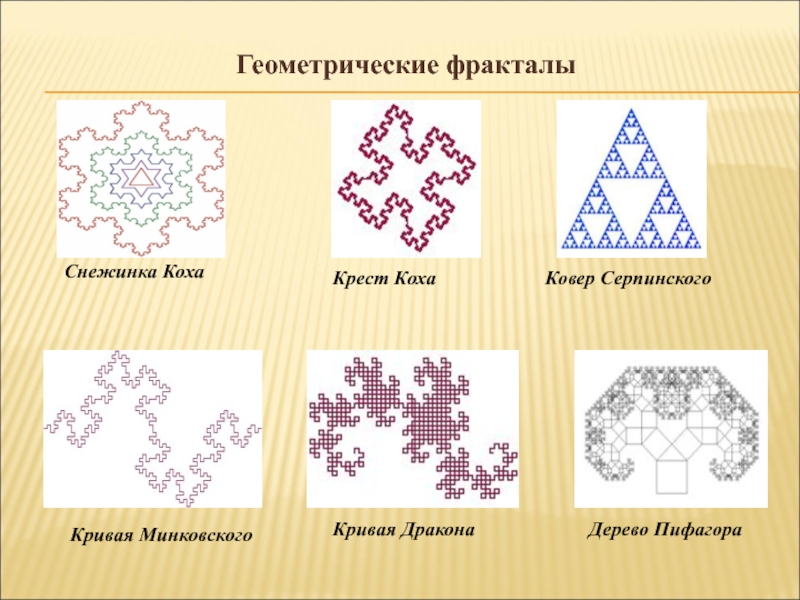
- 10. Геометрические фракталыСнежинка КохаКовер СерпинскогоКрест КохаКривая МинковскогоКривая ДраконаДерево Пифагора
- 11. Многогранник Эшена
- 12. Алгебраические фракталыАлгоритм построения алгебраических фракталов: многократный (итерационный)
- 13. Стохастические фракталыСтохастические фракталы получаются в том случае,
- 14. Практическое применение фракталовПрименение фракталов в науке и
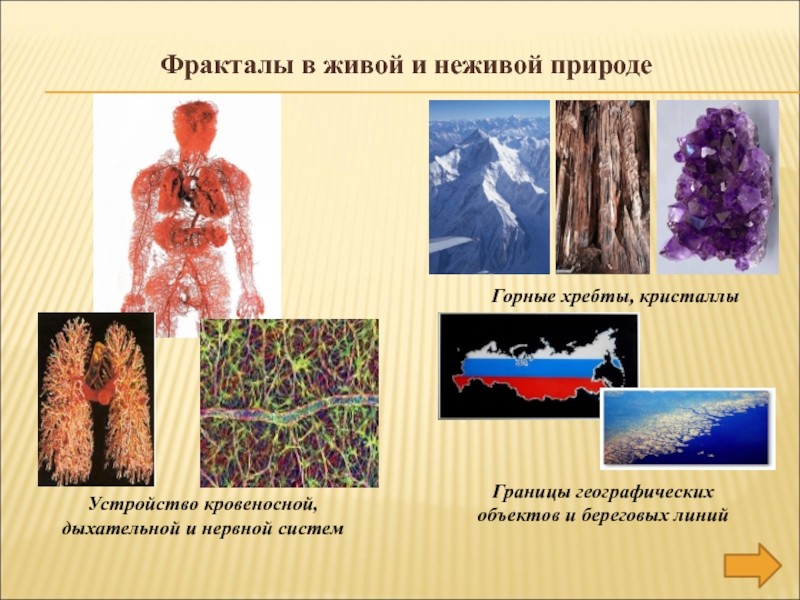
- 15. Фракталы в живой и неживой природеУстройство кровеносной,
- 16. Фракталы в живой и неживой природеСнежинки, морозные узорыФорма облаков и молнииУстройство Галактики
- 17. Фракталы в растительном мире
- 18. Фракталы в подводном миреКораллыОсьминогиМорская раковина
- 19. Фракталы в народном творчестве
- 20. Скачать презентанцию
«Есть в математике нечто, вызывающее человеческий восторг» Феликс Хаусдорф«Фракталы – геометрия красоты»
Слайды и текст этой презентации
Слайд 1МИНИСТЕРСТВО ОБРАЗОВАНИЯ ОМСКОЙ ОБЛАСТИ
БПОУ ОО «Омский промышленно-экономический колледж»
Индивидуальный проект
«Фракталы
– геометрия красоты»
Слайд 2«Есть в математике нечто, вызывающее человеческий восторг»
«Фракталы – геометрия красоты»
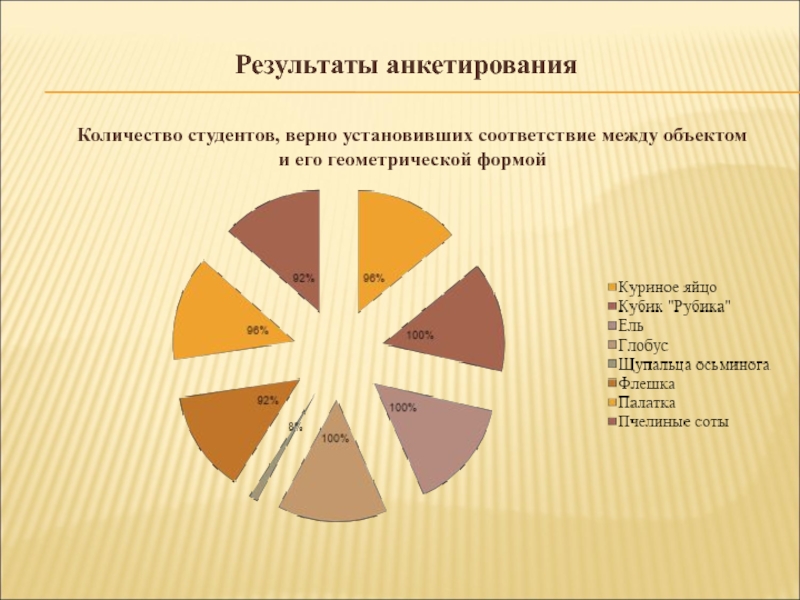
Слайд 4Результаты анкетирования
Количество студентов, верно установивших соответствие между объектом и его
геометрической формой
Слайд 5Актуальность исследования обусловлена противоречием между масштабным распространением фракталов в окружающем
нас мире и слабым представлением студентов об объектах фрактальной геометрии.
Цель:
изучить понятие «фрактал» и области его применения.Задачи:
На основе анализа литературы раскрыть понятие «фрактал», историю становления фрактальной геометрии, классификацию фракталов.
Рассмотреть природные явления и объекты окружающего мира с точки зрения фрактальной геометрии.
«Фракталы – геометрия красоты»
Слайд 6Объект:
Человек, математические абстракции, созданные человеком, изобретения человека, окружающий мир.
Предмет: Форма
и строение исследуемых предметов и явлений.
Методы исследования: анализ литературы, анкетирование.
«Фракталы
– геометрия красоты»
Слайд 7Бенуа Мандельброт
(1924-2010)
Теоретические основы фрактальной геометрии
Фрактал (от латинского fractus — дроблёный,
изрезанный) — это объект, обладающий свойством самоповторения: отдельные его части
повторяют форму и свойства всего объекта в целом на любом масштабном уровне.«Фракталом называется структура состоящая из частей, которые в каком то смысле подобны целому»
Слайд 8Теоретические основы фрактальной геометрии
Фрактал характеризуется следующими особенностями:
обладает сложной структурой при
любом увеличении,
является приближенно самоподобной,
обладает дробной хаусдорфовой размерностью,
может быть построен рекурсивными
процедурами. 
Слайд 10Геометрические фракталы
Снежинка Коха
Ковер Серпинского
Крест Коха
Кривая Минковского
Кривая Дракона
Дерево Пифагора
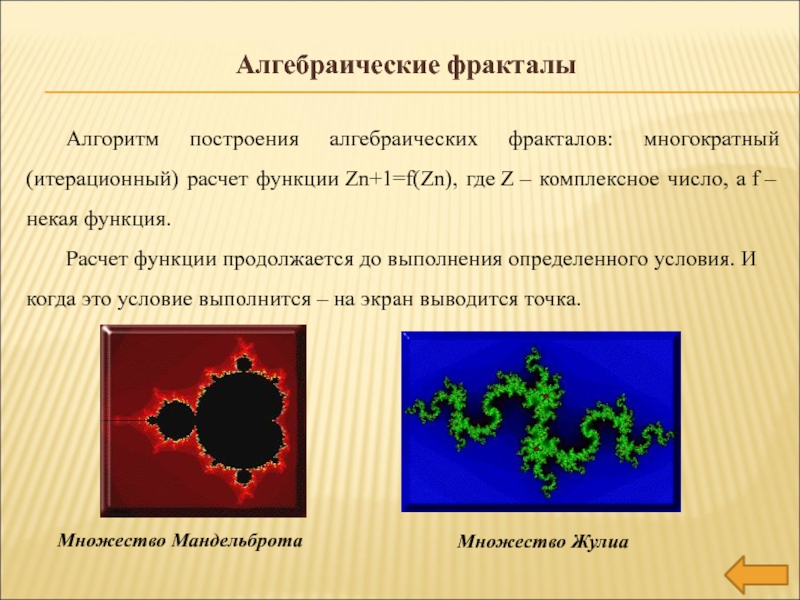
Слайд 12Алгебраические фракталы
Алгоритм построения алгебраических фракталов: многократный (итерационный) расчет функции Zn+1=f(Zn), где Z –
комплексное число, а f – некая функция.
Расчет функции продолжается до выполнения
определенного условия. И когда это условие выполнится – на экран выводится точка. Множество Мандельброта
Множество Жулиа
Слайд 13Стохастические фракталы
Стохастические фракталы получаются в том случае, если в итерационном
процессе случайным образом менять какие-либо его параметры.
Плазма
Слайд 14Практическое применение фракталов
Применение фракталов в науке и технике:
в компьютерных системах
в
графике
в телекоммуникации
в механике жидкостей
в физике поверхностей
в медицине
в биологии
в экономике
в
литературеРаспространение фракталов в живой и неживой природе
Фрактальные объекты народного творчества
Слайд 15Фракталы в живой и неживой природе
Устройство кровеносной, дыхательной и нервной
систем
Горные хребты, кристаллы
Границы географических объектов и береговых линий
Слайд 16Фракталы в живой и неживой природе
Снежинки, морозные узоры
Форма облаков и
молнии
Устройство Галактики
