Слайд 1Характеристики параллельных алгоритмов
Судаков А.А.
“Параллельные и распределенные вычисления” Лекция 13
Слайд 2План
Распараллеливание
Характеристики алгоритмов
Основные теоремы
Факторы снижения эффективности распареллеливания
Слайд 3Алгоритмы
Алгоритм – набор действий, которые необходимо выполнить для решения задачи
Последовательный
алгоритм – решение задачи на одном процессоре
Параллельный алгоритм – решение
задачи на одновременно работающих процессорах
Распараллеливание – какие операции должен выполнить каждый процессор параллельной системы
Слайд 4Декомпозиция, Связь, Синхронизация
Декомпозиция – разбиение задачи на составные части
Декомпозиция данных
Декомпозиция
функций
Комбинированная декомпозиция
Связь – взаимодействия между составными частями задачи
Синхронизация – обеспечение
того, что в некоторый момент все процессоры находятся в строго определенном состоянии
Слайд 5Эффективность распараллеливания
Единственная цель распараллеливания – уменьшение времени вычислений
Не все задачи
одинаково эффективно распараллеливаются
Задачи теоретического анализа
найти оптимальный метод распараллеливания для
данного алгоритма
Определить насколько та или иная схема эффективна
Слайд 6Модель
Система с p процессорами
Процессоры могут взаимодействовать между собой
В модели с
общей памятью
каждый процессор может обращаться независимо к каждой ячейке
памяти
При обращении к одной и той же ячейке на запись могут возникать конфликты
В модели с распределенной памятью
Каждые 2 процессора могут взаимодействовать между собой
CPU1
CPU2
CPU3
CPUp
коммутатор
CPU1
CPU2
CPU3
CPUp
память
Слайд 7Характеристики алгоритмов
Время вычисления на одном процессоре
Время вычисления на p
процессорах
Количество операций последовательного алгоритма N1
Количество операций параллельного алгоритма Np
Время
выполнения одной арифметической операции
Слайд 8Характеристики эффективности распараллеливания
Коэффициент ускорения
Во сколько раз время параллельный алгоритм быстрее
Идеальное
ускорение
Идеальное ускорение = количеству процессоров
Коэффициент эффективности
Отношение полученного ускорения
к идеальному
Какой процент процессоров работает
Коэффициент избыточности
Параллельный алгоритм может потребовать дополнительных операций
Качество распараллеливания
Произведение всех коэффициентов
Слайд 9Характеристики системы обмена информацией
Время передачи единицы информации
Время начальной задержки
Латентность
Время
установления связи
Отношение между временем обработки и временем передачи единицы информации
Отношение
между временем обработки единицы информации и временем установления связи
Слайд 10Масштабируемость (количество операций алгоритма)
Программы (алгоритмы) работают со входными данными
Чем больше
данных, тем дольше они будут обрабатываться
Масштабируемость – во сколько раз
возрастет время выполнения алгоритма при увеличении количества данных
Слайд 11Характеристики масштабируемости
Характерная размерность задачи
Количество входных данных
Количество операций алгоритма
Нотация большого O
Как
ведет себя количество N(n) при стремлении объема входных данных к
бесконечности
n
N(n)
O(n)
Слайд 12Примеры характерных размерностей
Количество элементов массива n
Размер квадратной матрицы nxn
Слайд 14Другие характеристики
Производительность системы
Цена алгоритма
Суммарные затраты процессорного времени
Слайд 15Основные свойства параллельных алгоритмов
На сколько вообще можно ускорить вычисления за
счет параллельной обработки?
Какое оптимальное количество процессоров ?
…
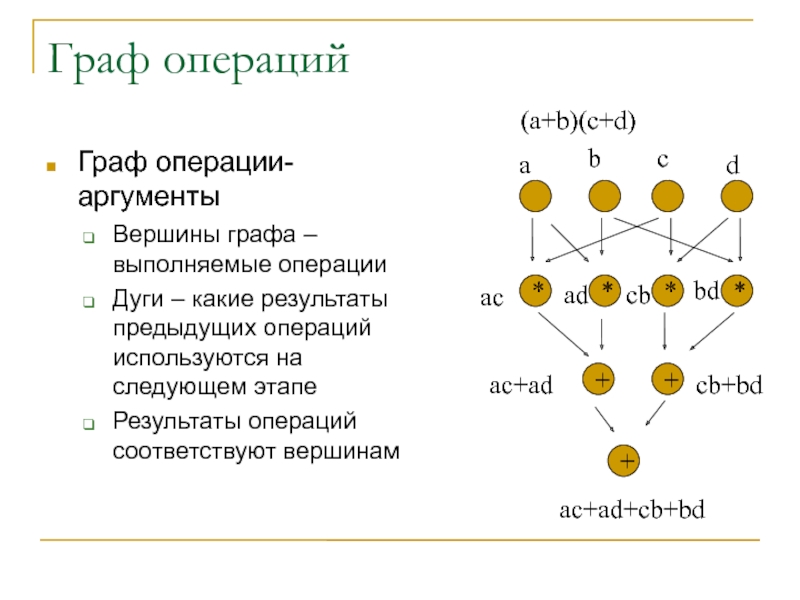
Слайд 16Граф операций
Граф операции-аргументы
Вершины графа – выполняемые операции
Дуги – какие результаты
предыдущих операций используются на следующем этапе
Результаты операций соответствуют вершинам
*
*
*
*
+
+
+
(a+b)(c+d)
a
b
c
d
ac
ad
cb
bd
ac+ad
cb+bd
ac+ad+cb+bd
Слайд 17Постановка задачи в терминах графа
Последовательности операций соответствует путь на
графе
Параллельно могут быть выполнены те операции, между которыми нет пути
на графе
Каждой схеме распараллеливания на p процессоров соответствует расписание:
Для операции i
Выбирается процессор Pi
В момент времени ti
Задача: Найти оптимальное расписание для распараллеливания
Слайд 18Пример расписания (общая память)
Момент времени 1
H=(операция 1:загрузить а, процессор 1,
момент1 )
H=(операция 2:загрузить b, процессор 2, момент1 )
H=(операция 3:загрузить c,
процессор 3, момент1 )
H=(операция 4:загрузить d, процессор 4, момент1 )
Момент времени 2
H=(операция 5: а*с, процессор 1, момент2 )
H=(операция 6: а*b, процессор 2, момент2 )
H=(операция 7: c*d, процессор 3, момент2 )
H=(операция 8: b*d, процессор 4, момент2 )
Момент времени 3
H=(операция 9: а*с+b*d, процессор 2, момент3 )
H=(операция 10: a*d+b*c, процессор 3, момент3 )
Момент времени 4
H=(операция 11: а*с+b*d+ a*d+b*c, процессор 3, момент4 )
Слайд 19Ограничения на расписание
В один и тот же момент времени один
процессор не может выполнять разные операции
Если для выполнения следующей операции
должен быть готов результат предыдущей
Момент выполнения следующей операции должен быть больше момента выполнения предыдущей операции
Слайд 20Определение времени выполнения параллельного алгоритма
Время выполнения соответствует максимально длинному пути
графа
Соответствует максимально возможному моменту времени, когда была назначена операция +
время выполнения операции
Для практики интересно
минимальное время при данной схеме вычислений
Минимальное время для всех схем вычислений
Минимально возможное время при неограниченном количестве процессоров
Слайд 21Некоторые свойства параллельных алгоритмов
Минимальное время выполнения параллельного алгоритма соответствует максимальной
длине пути (диаметру) графа
Для любого количества процессоров справедлива оценка времени
выполнения
Слайд 22Доказательство 2
Пусть есть расписание для получения минимально возможного времени
пусть оно
соответствует P процессорам
Пусть оно требует времени T∞
Пусть каждый последовательный шаг
этого расписания начинается в момент времени ti и всего шагов N∞
Пусть на каждом шаге выполняется ni операций
Общее время выполнения равно
Слайд 23Доказательство 2 (продолжение)
Рассмотрим, что будет если при выполнении того же
расписания у нас число процессоров равно p и не равно
оптимальному числу P
Тогда время выполнения нашего расписания либо возрастет (если p < P) либо останется неизменным (если p >= P)
Будем следовать нашему расписанию, но с меньшим количеством процессоров
На i-м шаге нам нужно выполнить ni операций
Каждому процессору необходимо выполнить последовательность операций на i-м шаге
Если p < P
p >= P 1
Слайд 24Доказательство 2 (продолжение)
Время выполнения алгоритма на p процессорах на i-м
шаге
Оценим время выполнения всего алгоритма на p процессорах сверху
Доказано
Слайд 25Другие свойства
Можно показать, что максимально возможное ускорение при неизменном количестве
операций равно количеству процессоров
Если количество процессоров равно T1/T∞ то время
выполнения параллельного алгоритма не будет больше чем в 2 раза превышать оптимальное время выполнения при оптимальном расписании
Слайд 26Использование описания с помощью графов
Вычислительную схему необходимо выбирать с графом
минимального диаметра (минимальное время наиболее длинной последовательной операции)
Оценочное оптимальное количество
процессоров определяется величиной
Максимальное время выполнения можно оценить
Удобно использовать для формальной оценки эффективности известных вычислительных схем
Слайд 27Факторы ограничения и повышения производительности
Гипотеза Минского – принципиальная непараллельность алгоритма
Закон Амдала – наличие принципиально последовательных участков
Закон Густафсона – линейное
ускорение
Гетерогенность – дисбаланс нагрузки
Сверхлинейное ускорение – аппаратное и алгоритмическое
Слайд 28Гипотеза Минского
Пусть программа имеет p последовательных участков
Пусть переход на тот
или другой участок выполняется путем бинарного ветвления
Всего выполнится участков программы
Если
всю программу выполнять на p процессорах, то ускорение будет не больше, чем
Для некоторых эффективных последовательных алгоритмов гипотеза справедлива
Слайд 29Закон Амдала (Amdahl, 1967)
Наличие последовательных участков приводит к существенному снижению
производительности
Пусть есть система из p процессоров
Пусть есть алгоритм, который состоит
из участков, которые выполняются параллельно и участков, которые выполняются последовательно
Пусть доля последовательных частей равна α
Тогда доля параллельных частей равна (1- α)
Слайд 31Оценка времени выполнения
Время выполнения последовательного алгоритма
Время выполнения последовательной части параллельного
алгоритма
Время выполнения параллельной части алгоритма на p процессорах
Время выполнения всего
параллельного алгоритма
Слайд 32Коэффициент ускорения и эффективность
Ускорение
Эффективность
Время выполнения на паракомпьютере
Оптимальное количество процессоров
Слайд 34Примеры закона Амдала
Централизованная схема вычислений
Симметричная мультипроцессорная система
И другие суперкомпьютеры
Векторные, конвейерные
процессоры
Обмен данными
Слайд 35
Централизованная схема
Главный процессор раздает рабочим задачу
Рабочие выполняют задачу и возвращают
результат главному процессору
Главный процессор – узкое место – существенно последовательная
часть алгоритма
Главный процессор в один момент времени может обработать только данные с одного рабочего
Главный процессор
(master)
Рабочий
процессор
Рабочий
процессор
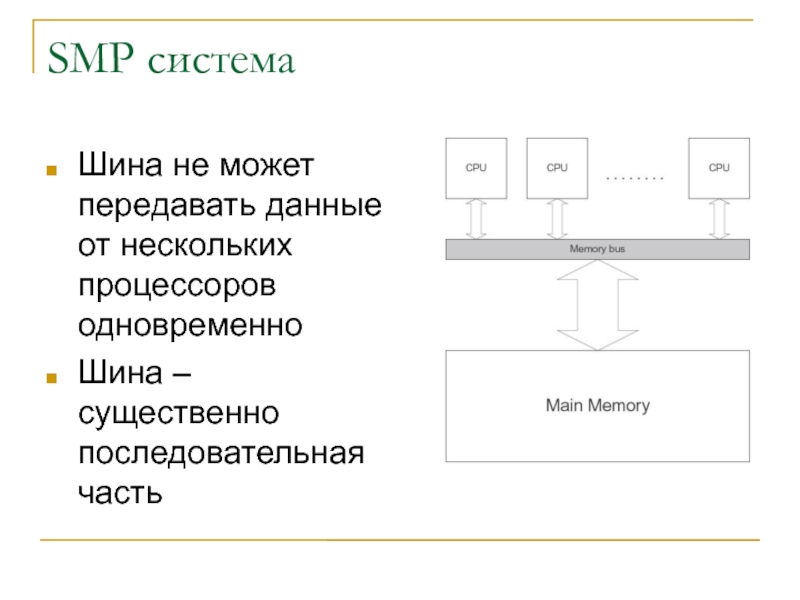
Слайд 36SMP система
Шина не может передавать данные от нескольких процессоров одновременно
Шина
– существенно последовательная часть
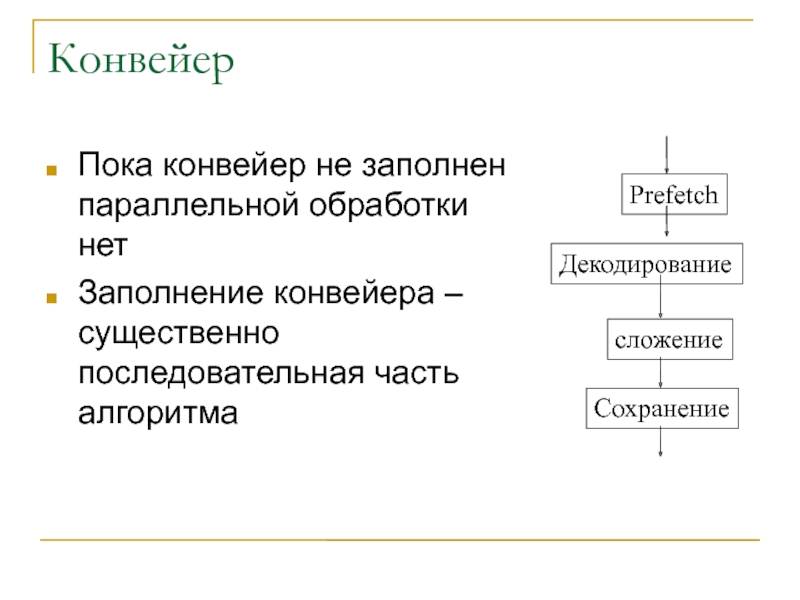
Слайд 37Конвейер
Пока конвейер не заполнен параллельной обработки нет
Заполнение конвейера – существенно
последовательная часть алгоритма
Prefetch
Декодирование
сложение
Сохранение
Слайд 38Закон Густафсона
Другая формулировка закона Амдала
Пусть параллельный алгоритм выполняется за
время Tp
Пусть β – доля существенно последовательных операций параллельного
алгоритма, тогда (1- β) – доля алгоритма, которая выполняется параллельно на p процессорах
Слайд 39Оценка времени для закона Густафсона
Время параллельной обработки
Время последовательной обработки (параллельная
часть выполняется в p раз медленнее)
Ускорение
Получили линейную масштабируемость
Слайд 40Связь или противоречие?
Используются разные параметры
Амдал – доля последовательных операций
последовательного алгоритма
Густафсон – доля последовательных операций параллельного алгоритма
Связь между параметрами
Доля последовательных вычислений зависит от количества процессоров и объема данных с которыми работает алгоритм!
При увеличении количества данных, с которыми работает алгоритм часто количество операций распараллеливаемой части растет быстрее, чем количество операций последовательной части и в явном виде закон Густафсона более применим
Для быстрых алгоритмов с малым количеством операций в явном виде лучше подходит закон Амдала
Слайд 41Практическое применение законов Амдала и Густафсона
При очень малом количестве
последовательных операций возможно очень большое ускорение при очень большом количестве
процессоров
При увеличении объемов данных с которыми работает алгоритм эффекимвность распараллеливания растет
Слайд 42Гетерогенность
Гомогенная система – все процессоры одинаковы
Гетерогенная система – процессоры
разные
Большинство алгоритмов рассчитаны на гомогенную систему
Слайд 43Дисбаланс нагрузки
Если алгоритм, рассчитанный на гомогенную систему запустить на гетерогенной,
то
Более быстрые процессоры выполнят свою работу быстрее
Более медленные процессоры
будут работать дольше
Время выполнения такой параллельной программы будет определяться самым медленным процессором!!!
Эффективность распараллеливания падает – часть процессоров простаивает
Слайд 44Балансировка нагрузки
Для решения проблемы используют балансировку нагрузки
Статическая – на этапе
запуска задачи учитывается производительность и загруженность
Динамическая – балансировка выполняется в
процессе работы
Слайд 45Сверхлинейное ускорение
Сверхлинейное ускорение – ускорение большее, чем количество процессоров
Согласно рассмотренной
теории – не возможно
Просто учли не все варианты
На практике встречается
!
Аппаратное сверхлинейное ускорение
Алгоритмическое сверхлинейное ускорение
Слайд 46Аппаратное сверхлинейное ускорение
Возможно, если процессоры параллельной программы выполняют параллельный код
с большей производительностью, чем последовательный
Каждый процессор параллельной системы может
выполнять
больше последовательных однотипных операций
Работать с меньшими объемами данных (за счет декомпозиции)
Данные и код лучше размещаются в оперативной памяти
Увеличивается вероятность попадания данных и кода в кэш
Очень часто встречается на практике для математических задач!!!
Слайд 47Алгоритмическое сверхлинейное ускорение
Возможно, когда для выполнения параллельного алгоритма
Необходимо выполнить меньше
операций
Не все операции
Часто встречается в задачах поиска, подбора
Слайд 48Пример: подбор пароля
Пусть последовательный алгоритм поиска имеет p стадий
Стадия1: Перебор
географических названий
Стадия2: Перебор нецензурных слов
Стадия3: Перебор компьютерных терминов
…
Последовательный алгоритм выполняет
все стадии последовательно и в случае успеха останавливается
Слайд 49Параллельный алгоритм подбора
Каждый процессор выполняет свою стадию
Процессор1 : Стадия1
Процессор2: Стадия
2
…
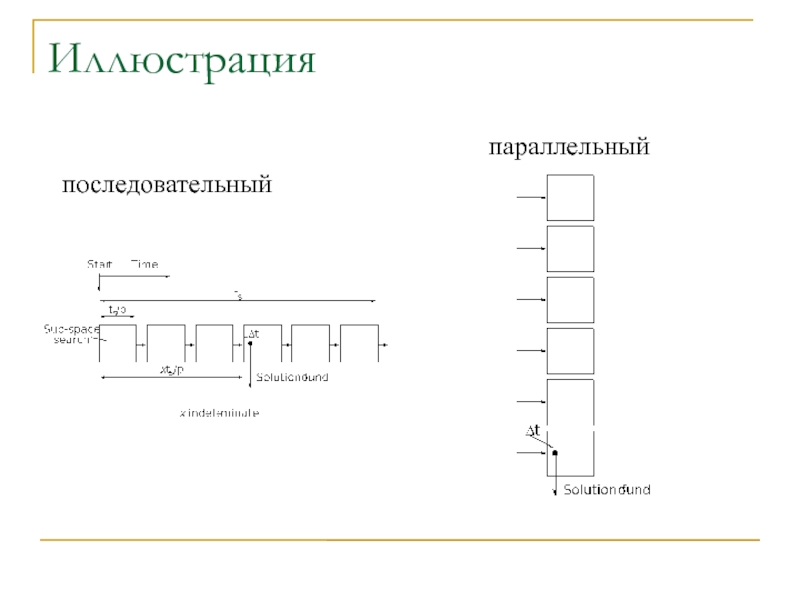
Слайд 50Иллюстрация
последовательный
параллельный
Слайд 51Счастливый случай
Как правило пользователи выбирают пароли, чтобы лучше запоминались
Если на
какой-либо стадии поиска поиск выполняется в нужной категории, то скорее
всего пароль будет подобран быстро
Слайд 52Оценка времени последовательного алгоритма
Пусть последовательный алгоритм найдет результат в k-й
стадии через время Δt
Время выполнения одной стадии t
Время выполнения последовательного
алгоритма
Слайд 53Оценка времени параллельного алгоритма
Процессор параллельной системы, который выполняет k-ю стадию
сразу найдет нужный результат за время Δt
Все остальные процессоры могут
прекратить работу
Слайд 54Ускорение
Коэффициент ускорения
Сверхлиненейное ускорение возможно, когда ускорение больше p
Условие
Если успешный подбор
будет сразу же после начала стадии
На практике очень вероятно, учитывая,
как пользователи выбирают пароли
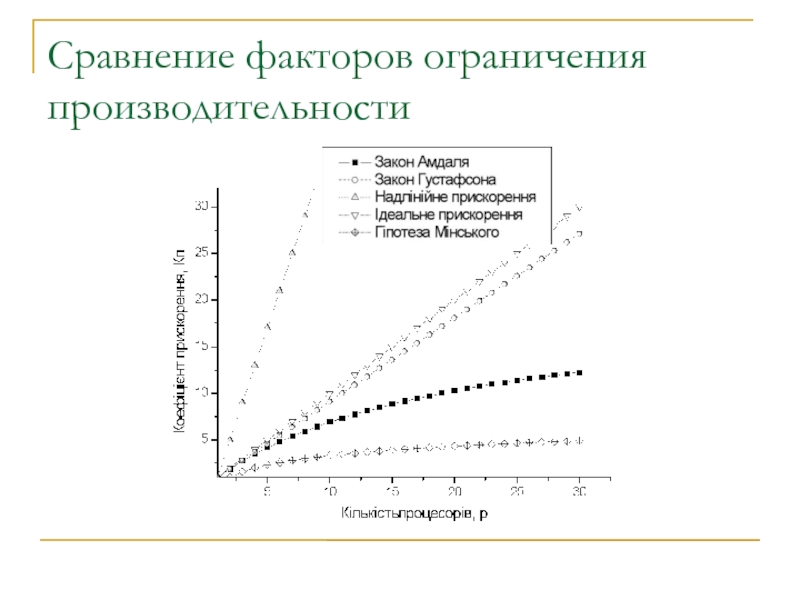
Слайд 55Сравнение факторов ограничения производительности
Слайд 56Выводы
В большинстве случаев ускорение за счет распараллеливания не может быть
больше количества процессоров
Обычно ускорение значительно меньше количества процессоров
На практике встречаются
ситуации, когда возможно сверхлинейное или близкое к идеальному ускорение
При увеличении количества процессоров эффективность распараллеливания падает
Для каждой задачи существует свое оптимальное количество процессоров
При увеличении количества данных и количества операций алгоритма решения задачи, эффективность распараллеливания увеличивается
Если задача эффективно и быстро решается на однопроцессорной системе, то переход к многопроцессорному алгоритму обычно не значительно увеличивает эффективность