Слайд 1Лекция
FloEFD: Моделирование пористых сред
Слайд 2Исследование течения в фильтрующей
установке
В данном разделе рассмотрена задача расчета течения
в фильтрующей колонне.
Постановка задачи
Рассмотрим фильтрующую колонну, геометрическая модель которой показана
на рис. 1, 2. Она состоит из бака и системы фильтров, представляющих собой стаканы с фланцами. Фильтры опираются на патрубки, соединенные с конической перегородкой. Из-за этого участки цилиндров на фильтрах, которые вставлены в патрубки, фактически не обладают проницаемостью.
Геометрическая модель фильтра в разнообразных масштабах показана на рис. 3-5. Как видно, конструкция является достаточно сложной. Боковые грани состоят из частых вертикальных ребер с цилиндрической навивкой трапецеидального сечения. Большее основание сориентировано на внешнюю по отношению к потоку сторону. Дно образовано повторяющимися прямолинейными элементами, сечение которых идентично использованным в навивке. Они соединены под прямым углом с набором параллельных ребер относительно небольшого размера, которые, в свою очередь, опираются на совокупность параллельных пластин. Такая схема придает конструкции достаточную жесткость.

Слайд 3Жидкость в колонне поступает из нижнего патрубка, поднимается вверх, затем
проходит через фильтры и выходит через левый верхний патрубок вниз.
Целью анализа является исследование течения (жидкости с характеристиками воды) и, в частности, расчет потоков через каждый фильтр вплоть до идентификации потоков через дно и цилиндрические стенки.
Также нас интересует величина потери давления при прохождении жидкости через стенки фильтров.
Рис. 1. Геометрическая модель колонны —
разрез вертикальной плоскостью
Рис. 2. Модель колонны — фрагмент
Слайд 4Рис. 3. Геометрическая модель фильтра —
исходный вариант
Рис. 4. Геометрическая модель
фильтра
— фрагмент
Рис. 5. Геометрическая модель фильтра — увеличенный фрагмент
Слайд 5Получение характеристик пористой среды
Основной проблемой при моделировании течения в подобных
системах является радикальное различие масштабов: проходное сечение витками проволоки навивки
составляет 0,25 мм, при том что габариты колонны измеряются метрами. В COSMOSFloWorks для объектов с подобным различием масштабов применяется семейство настроек Narrow Channel (Узкие каналы), однако число протяженных по периметру цилиндра щелей составляет несколько сотен. Поэтому необходимо использовать такую сущность, как Porous Medium (Пористая среда), представляющую собой "гомогенизированную" модель структурно-неоднородной среды, образованной периодическими объектами. COSMOSFloWorks содержит несколько типов пористых сред:
изотропная — имеет одинаковую проницаемость во всех направлениях;
однонаправленная — имеет проницаемость только в одном направлении;
осесимметричная — для нее назначается проницаемость в осевом и в радиальном направлении (в окружном направлении массопереноса нет);
ортотропная — проницаемость назначается персонально относительно каждого из трех взаимно ортогональных направлений.

Слайд 6Моделируются пористые материалы, у которых составляющие коэффициента проницаемости k по
характерным направлениям определяются одной из следующих их зависимостей от параметров
течения:
k = Δp×S (m× L), где Δp — перепад давления между противоположными сторонами пористого тела в некотором направлении; m — массовый расход текучей среды в этом направлении; S и L — площадь поперечного сечения и длина пористого тела в этом направлении. Величина k, если браться ее идентифицировать, задается зависимостью ΔP от m и константами S и L. Если вместо массового расхода m задан объемный расход v, то определяется m=v×ρ, где ρ — плотность текучей среды;
k = ( A×v + B) ρ , где v — скорость текучей среды; ρ — плотность текучей среды; A и B — константы. Величина k определяется константами A и B, а V и ρ вычисляются после построения модели течения (или, само собой, реального эксперимента);
k = μ (ρ × D), где μ и ρ — коэффициент динамической вязкости и плотность текучей среды; D — характерный размер поры, обычно определяемый из экспериментов;
k = μ (ρ × D) × f (Re) , где, в отличие от предыдущей формулы, фигурирует
f (Re) — функция от числа Рейнольдса. Пользователь может выбрать различные варианты зависимости, в частности адаптированную для турбулентного течения в узких каналах круглой формы с гладкими стенками — соответствующие зависимости приводятся в справочной системе расчетного модуля.

Слайд 7Мы остановимся на варианте, в котором коэффициент проницаемости линейно зависит
от скорости и плотности. Нужно установить коэффициенты А и B,
чтобы определить в базе данных эквивалентный пористый материал.
В дополнение к имеющемуся соотношению k = ( A× v + B) / ρ примем во внимание собственно определение коэффициента проницаемости:
k = − grad ( p) / (ρ× v).
Приравнивая правые части уравнений, получаем выражение для градиента давления при прохождении текучей среды через однородную пористую среду:
grad ( p) = A× v2 + B × v.
Геометрическая модель для проведения виртуальных экспериментов по определению коэффициентов в уравнении проницаемости показана на рис. 6. Данная модель предназначена для имитации прохождения текучей среды через цилиндрические стенки фильтра в направлении снаружи внутрь (свойства проницаемости, в общем случае, чувствительны к направлению движения). Ограничивающие секущие плоскости выбирались так, чтобы сохранить геометрическую симметрию относительно них. В месте сопряжения вертикального ребра с кольцевой обмоткой геометрия сечения ребра изменена, чтобы избежать контакта по линии (она получалась бы при соприкосновении полного скругления на клиновидном ребре с цилиндрической гранью обмотки). В данном случае относительно малая площадка контакта реализована в виде фрагмента цилиндрической грани с осью, совпадающей с осью фильтра (рис. 7).

Слайд 8Рис. 6. Геометрическая модель для определения констант
в уравнении проницаемости
Рис. 7.
Фрагмент геометрической модели в сечении плоскостью,
перпендикулярной оси симметрии
Слайд 9Граничные условия внутри полости показаны на рис. 8. Наружное давление
назначено в варианте Total Pressure (Полное давление), поскольку здесь предполагается
вход среды. На предполагаемом выходе назначено условие Environment Pressure (Давление внешней среды). Именно такое сочетание рекомендуется для задач, в которых, как на входе, так и на выходе, используются граничные условия в виде назначенного давления. Условие в виде сочетания давлений представляется ближе к постановке конкретной задачи, требующей установить зависимость падения давления от скорости. Поскольку проходное сечение не является постоянным, скорость также меняется. Поэтому назначенная на входе (выходе) скорость потребует пересчета в месте расположения фильтра. Если сечение постоянно, то назначение скорости на входе (выходе) смотрелось бы более логично.
На боковых стенках поставлено условие Ideal Wall (Идеальная стенка), реализующее взаимодействие текучей среды со стенкой без трения. В принципе, на верхней и нижней гранях расчетного домена, огранивающих полость, можно было бы поставить условие Periodicity (Периодичность), однако в данной ситуации отличия были бы малозначимы. Поэтому, исходя из соображений единообразия между направлениями периодичности (требовалась бы циклическая симметрия/периодичность), было выбрано более тривиальное условие.

Слайд 10Рис.8. Граничные условия
Рис.9. Начальная сетка
Слайд 11Начальная сетка показана на рис. 9. С целью рационального разбиения
в окрестности фильтра сделаны следующие настройки. На вкладке Basic Mesh
(Базовая сетка) (рис.10) изменено число ячеек вдоль каждого из направлений относительно настроек по умолчанию.
Рис. 10. Настройки начальной сетки — Базовая сетка
Слайд 12На вкладке Solid/Fluid Interface (Поверхность раздела твердых тел с текучей
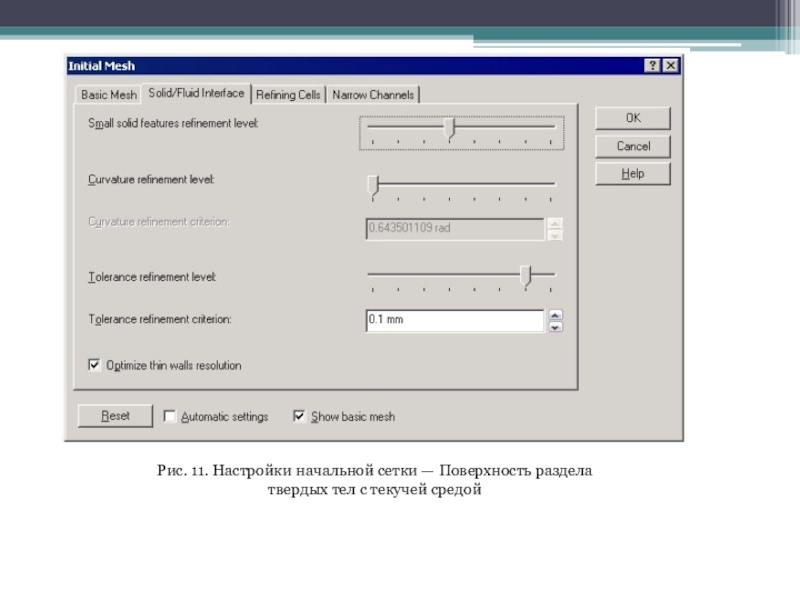
средой) (рис.11) c помощью регулятора Small solid feature refinement level
(Уровень разрешения сеткой мелких особенностей модели), принимающего дискретные положения 0−7, задан максимальный допустимый уровень дробления ячейки базовой сетки. Так удовлетворяется критерий разрешения, который заключается в том, что максимальный угол между нормалями к поверхности модели в отдельно взятой расчетной ячейке не должен превышать 120°. В данном случае установлен уровень дробления ячеек 3. Также регулятор Tolerance refinement level (Уровень разрешения сеткой выступов поверхности), управляющий уровнем дробления ячейки базовой сетки для удовлетворения критерия разрешения начальной расчетной сеткой выступов поверхности модели, установлен в положение 6. При этом для параметра Tolerance refinement criterion (Критерий разрешения сеткой выступов поверхности), определяющего допустимую максимальную выпуклость поверхности модели в ячейке относительно плоского многоугольника, аппроксимирующего эту поверхность в ячейке, принято значение 0,1 мм. Мы ориентируемся на то, что минимальный размер основания трапеции в сечении навивки равен 1,1 мм, а радиусы наименьших скруглений имеют величину 0,2−0,3 мм.

Слайд 13Рис. 11. Настройки начальной сетки — Поверхность раздела
твердых тел с
текучей средой
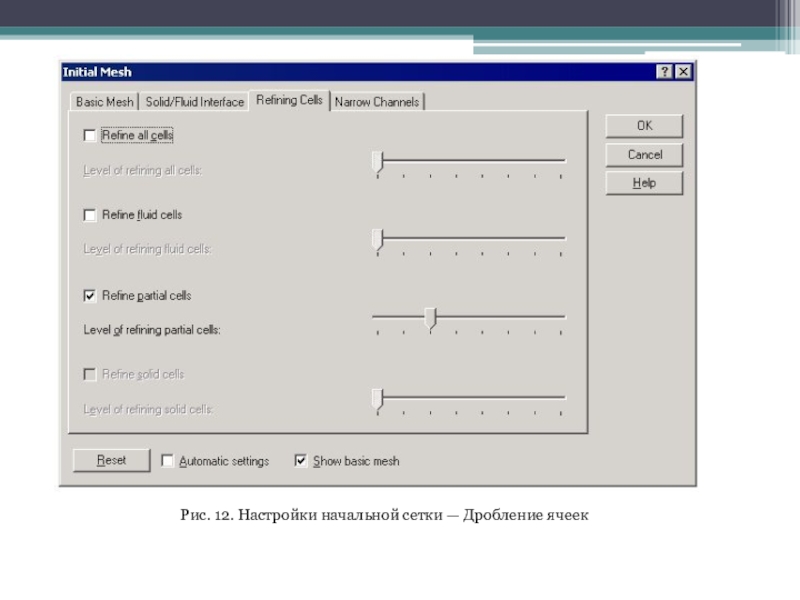
Слайд 14На вкладке Refining Cells (Дробление ячеек) (рис. 12) назначаем предельную
степень дробления ячеек базовой сетки, разделяемых текучей средой и телом.
Для этого активизируем опцию Refine partial cells (Дробить все частичные ячейки) и ползунковый переключатель Level of refining partial cells (Уровень дробления всех частичных ячеек) в положение 2.
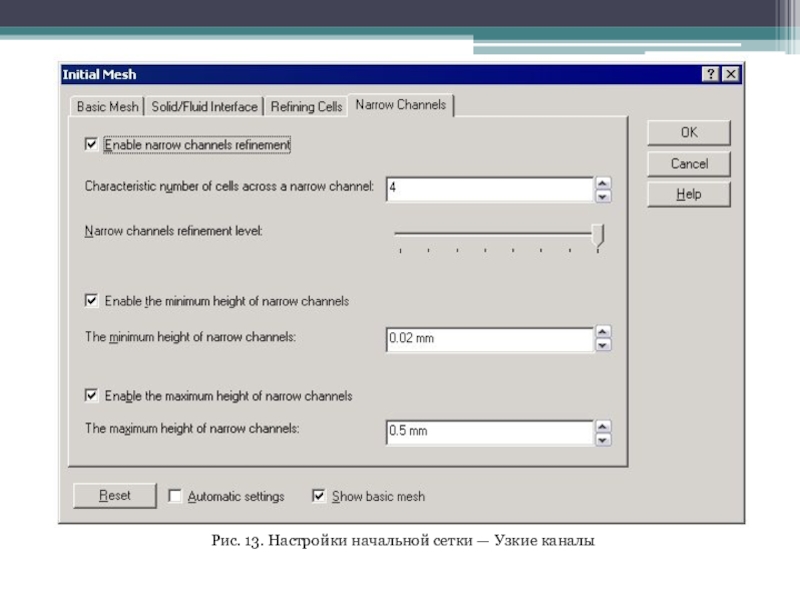
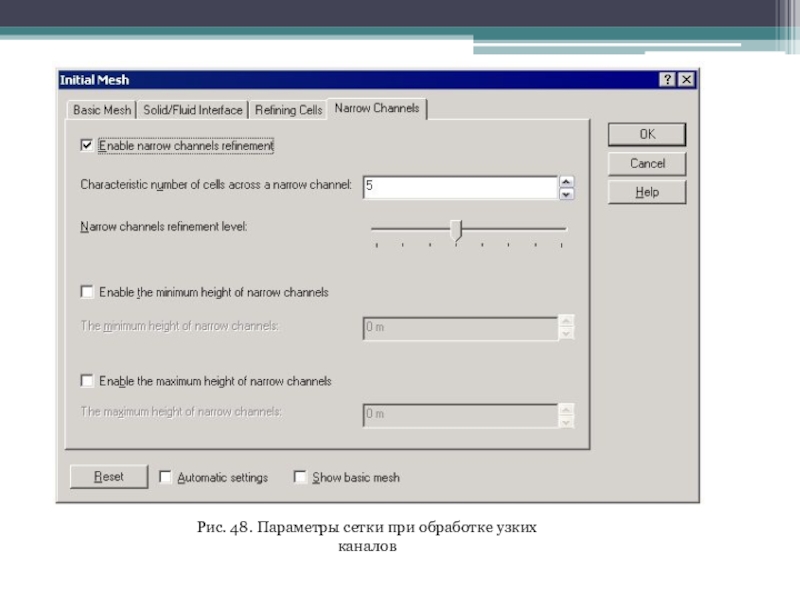
На вкладке Narrow Channels (Узкие каналы) (рис. 13), если отмечена опция Enable narrow channels refinement (Включить опцию дробления сетки в узких каналах), следует назначить параметры, определяющие дробление ячеек начальной расчетной сетки. Это позволит уточнить результат в проточных частях модели. В поле Characteristic number of cells across a narrow channel (Критическое число ячеек поперек узкого канала) задается минимальное число ячеек начальной расчетной сетки в текучей среде по нормали к поверхности модели до противоположной поверхности модели: если этих ячеек меньше, то они дробятся. C помощью регулятора Narrow channel refinement level (Уровень дробления сетки в узких каналах) назначаем максимальный уровень дробления ячейки базовой сетки для удовлетворения критерия Characteristic number of cells across a narrow channel (Критическое число ячеек поперек узкого канала): положение бегунка N от 0 до 7 означает, что допустимый минимальный размер ячейки начальной сетки при попытках удовлетворить этот критерий в 2N раз меньше размера ячейки базовой сетки по каждой из осей глобальной системы координат. В данном случае максимально возможный уровень дробления адекватен воспроизведению состояния потока в фильтре.

Слайд 15Рис. 12. Настройки начальной сетки — Дробление ячеек
Слайд 16Также задействуем опции Enable the minimum height of narrow channels
(Задать минимальную высоту узкого канала) и Enable the maximum height
of narrow channels (Задать максимальную высоту узкого канала), назначая для управляющих полей The minimum/maximum height of narrow channels (Минимальная/максимальная высота узкого канала) значения 0,02 и 0,5 соответственно. Нижняя граница определяет минимальный зазор, интерпретируемый как "узкий" канал. Он назначен для того, чтобы в местах примыкания скругленных граней ребер к навивке не происходило нерационального дробления ячеек. Верхняя граница назначена, чтобы исключить "избыточное" дробление между вертикальными ребрами.
Слайд 17Рис. 13. Настройки начальной сетки — Узкие каналы
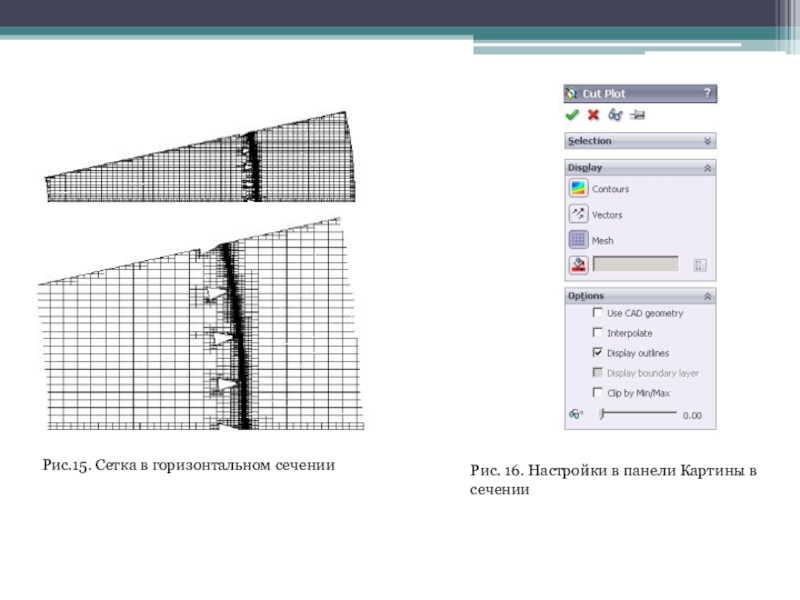
Слайд 18На рис. 14, 15 показана расчетная сетка в вертикальном и
горизонтальном сечении. Настройки сечения в панели Cut Plot (Картины в
сечении) показаны на рис. 16. Как видно, отключена опция Interpolate (Интерполировать) между центрами ячеек расчетной сетки (это, в частности, ускоряет просмотр диаграммы), так что в пределах каждой ячейки результаты расчета будут показаны постоянными. Также отключена опция Use CAD geometry (Использовать геометрию САПР) —при просмотре результатов расчета будет показана геометрия САПР в том виде, в котором она разрешена расчетной сеткой.
Рис. 14. Сетка в вертикальном сечении
Слайд 19Рис.15. Сетка в горизонтальном сечении
Рис. 16. Настройки в панели Картины
в сечении
Слайд 20На сетке в вертикальном сечении каналы между витками навивки вблизи
их узкого сечения разрешены удовлетворительно, а вот там, где основания
трапеций больше, получилось только две-три ячейки. Это, по всей видимости, произошло потому, что параметру The maximum height of narrow channels присвоена недостаточно большая величина — 0,5 мм, в то время как расстояние между вершинами трапеций изменяется от 1,3 до 0,3 мм. То есть процедура уплотнения сетки в узких каналах сработала вполне корректно, ограничившись теми зонами, где канал ýже, чем 0,5, но шире 0,02. Если бы пространство в широких участках было разрешено сеткой точнее, то более адекватным стало бы и представление криволинейных границ ребер: это произошло бы по той причине, что разница в уровнях разбиения смежных ячеек не может превысить единицу. То есть область уплотнения распространилась от каналов на большее расстояние.
В качестве целей назначаем объемный и массовый расход через вход и выход (это сделано для контроля сходимости интегральной величины потока), а также минимальную, среднюю и максимальную скорость на входе и выходе, что, как представляется, повысит качество расчета в локальных объемах и в области с текучей средой в целом.
Проанализируем результаты расчета для назначенной разницы давления (динамическое на входе минус статическое на выходе) 0,1 МПа. Диаграмма статического давления в сечении плоскостью, располагающейся между ребрами и перпендикулярной оси фильтра, показана на рис. 17.

Слайд 21Как видно, давление изменяется скачкообразно при протекании жидкости через фильтр.
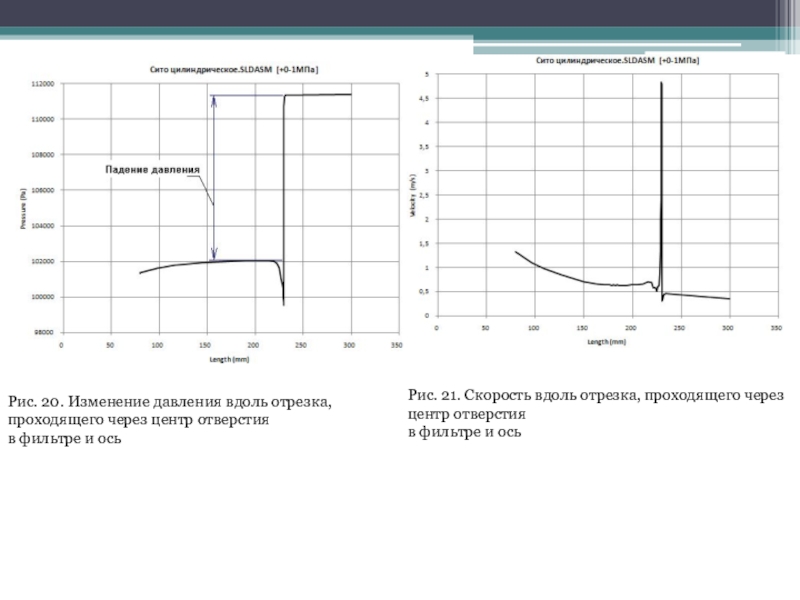
Более информативную картину можно получить, визуализировав распределение давления вдоль некоторой
траектории. В данном случае это линия эскиза, проходящего через точку, расположенную посередине, как между навивкой, так и между ребрами (рис. 18). Здесь следует иметь в виду, что в модели на рис. 19 движение жидкости происходит слева направо, а на графике — справа налево (рис. 20).
Как видно, давление постоянно при движении от входа до фильтра, после чего при прохождении через фильтр происходит его уменьшение до некоторой величины, причем собственно на фильтре наблюдается локальное падение давления. Последний эффект обусловлен локальным же скачком скорости, как это показано на рис. 20.
Рис. 17. Поле скоростей в сечении, проходящем через ось
Слайд 22Рис. 18. Эскиз для графика вдоль линии
Если не учитывать местное
изменение скорости, то величина падения давления Δp идентифицируется, как на
иллюстрации. Тогда градиент давления на фильтре: grad ( p) = Δp / δ.
Здесь δ — толщина фильтрующего объекта. Это в некотором смысле условная величина, поскольку в ряде случаев она однозначно не идентифицируется. Примем ее равной размеру (в радиальном направлении) подмотки в совокупности с вертикальными ребрами (см. рис. 19). Чтобы "толщина" (7 мм) в зависимостях для определения констант фильтрующей среды стала объективной характеристикой, следует ее же использовать в дальнейшем при назначении параметров виртуальных сущностей.
Рис. 19. Условная толщина пористой среды
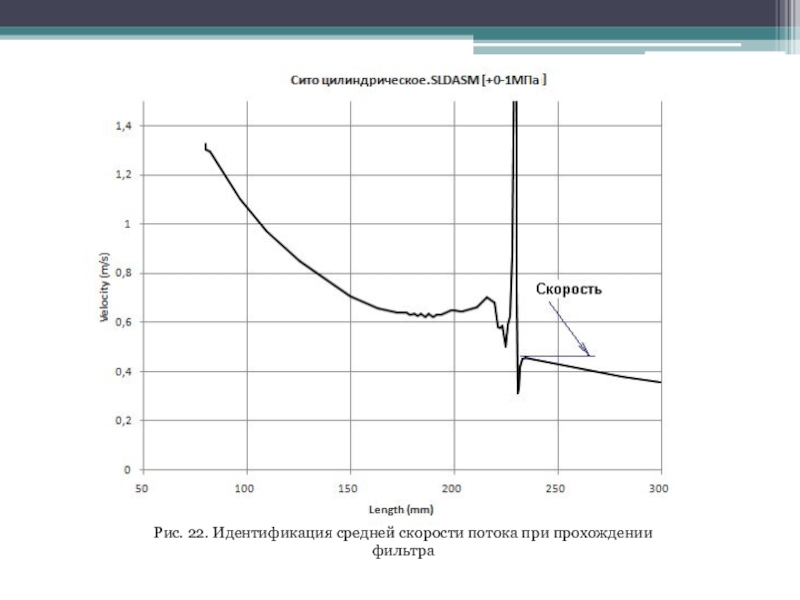
Слайд 23Определенная неоднозначность выявляется при попытке идентифицировать скорость потока при прохождении
через фильтр (в последующем — пористую среду).
В данном случае нам
нужна средняя скорость. Однозначный алгоритм ее получения предложить достаточно сложно. Мы будем принимать эту скорость равной максимальному значению скорости потока вдоль траектории на участке диаграммы, исходящем от входа (рис. 21). Эта проблема, кстати говоря, возникла потому, что расчетная область является (в сечении горизонтальной плоскостью) сектором, из-за чего скорость, даже в отсутствие фильтра, непостоянна. Если бы, как это имеет место при расчете "эффективных" характеристик пористой среды, имитирующей дно фильтрующего цилиндра, сечение проточной части было постоянным (расчетная область — параллелепипед), то средняя скорость была бы равна скорости на входе/выходе.
Слайд 24Рис. 20. Изменение давления вдоль отрезка, проходящего через центр отверстия
в
фильтре и ось
Рис. 21. Скорость вдоль отрезка, проходящего через центр
отверстия
в фильтре и ось
Слайд 25Рис. 22. Идентификация средней скорости потока при прохождении фильтра
Слайд 26Определенный интерес представляет диаграмма скорости в сечении, перпендикулярном оси и
проходящем посередине между витками. Изображение на рис. 23 свидетельствует о
том, что функция отслеживает предполагаемые (при условии стационарного характера течения, который, кстати говоря, нами не аргументирован) направления симметрии относительно плоскостей, проходящих через ось. При этом расчетная сетка является ортогональной и потенциальную симметрию результатов никак не "стимулирует".
Рис. 23. Поле скоростей в сечении, перпендикулярном оси
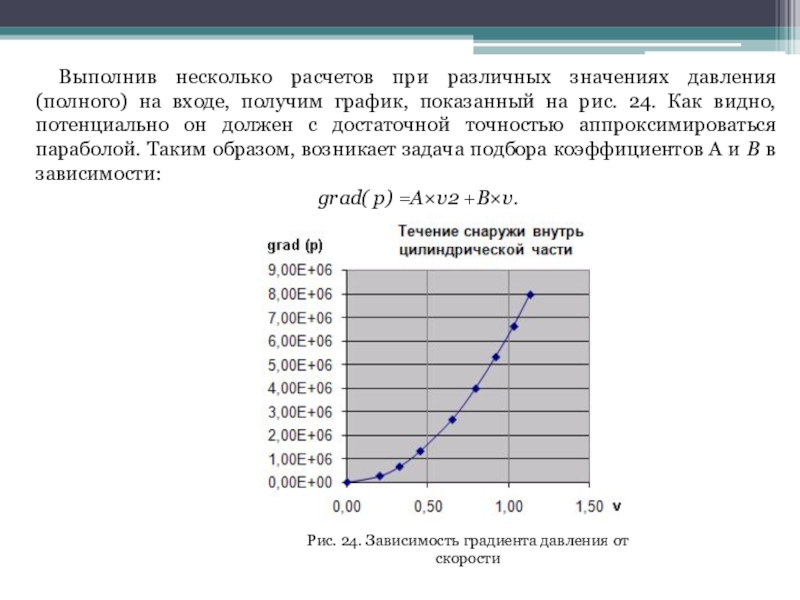
Слайд 27Выполнив несколько расчетов при различных значениях давления (полного) на входе,
получим график, показанный на рис. 24. Как видно, потенциально он
должен с достаточной точностью аппроксимироваться параболой. Таким образом, возникает задача подбора коэффициентов А и B в зависимости:
grad( p) =A×v2 +B×v.
Рис. 24. Зависимость градиента давления от скорости
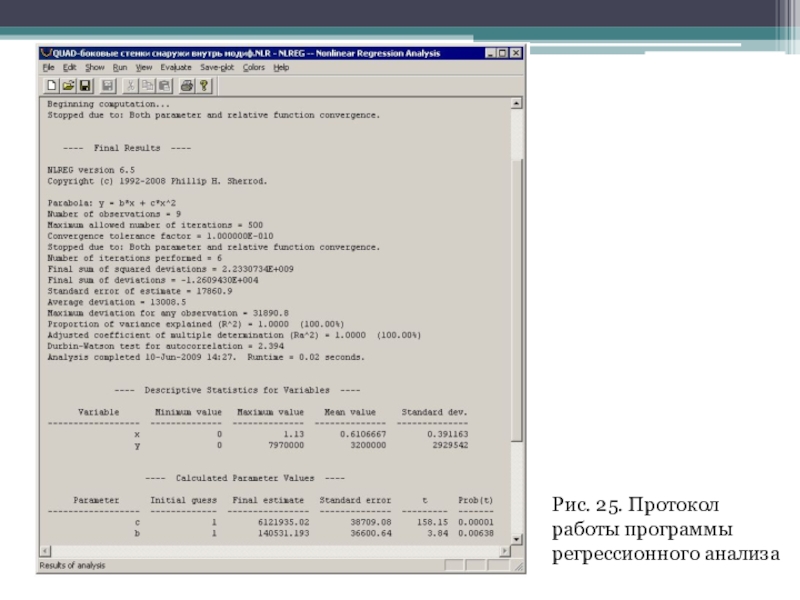
Слайд 28Для этого привлекаем программу NLREG, заимствованную нами с сайта http://www.nlreg.com.
Она предназначена для нелинейного регрессионного анализа и аппроксимации функций. Программа
в течение 30 дней функционирует в бесплатном режиме, что позволяет выполнить минимально необходимый объем вычислений.
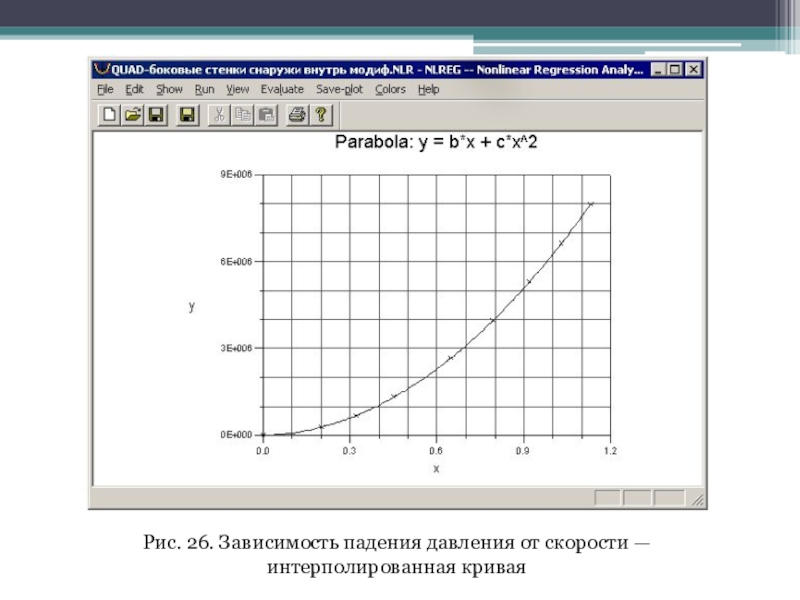
Протокол работы программы регрессионного анализа показан на рис. 25, а воспроизведенный график параболической функции с наложенными на него "экспериментальными" точками — на рис. 26. Как видно, параболическая аппроксимация зависимости падения давления от скорости в широком диапазоне варьирования градиента давления оказалась вполне адекватной.
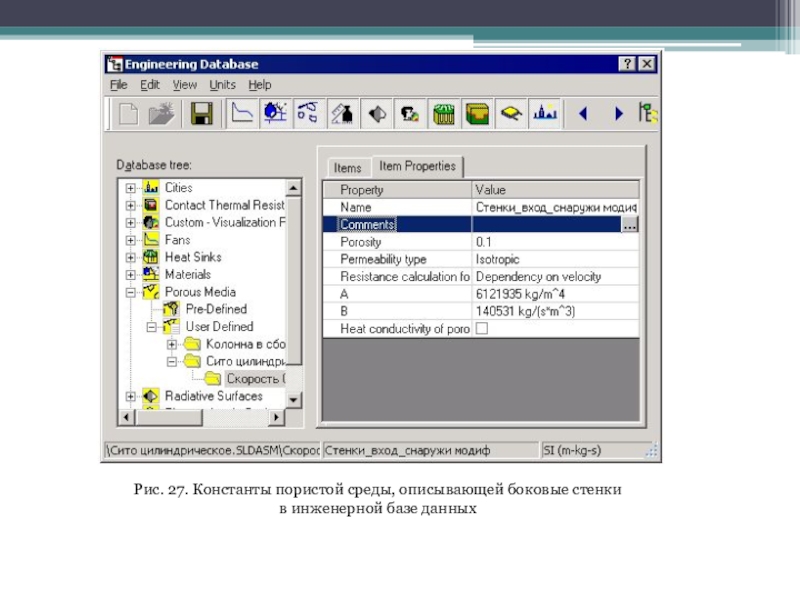
Рассчитанные константы изотропной пористой среды помещаются в инженерную базу данных. Для виртуальной среды, имитирующей боковые стенки, окно со свойствами показано на рис. 27. Здесь поле Porosity (Пористость) с точки зрения собственно расчета несет сугубо иллюстративный смысл, но при отображении результатов его смысл вполне конкретен.
Следует еще раз подчеркнуть, что приведенные характеристики виртуальной пористой среды определены для случая, когда жидкость течет снаружи цилиндра внутрь. В реальной модели возможна ситуация, когда на отдельных участках поток следует в противоположном направлении. Из-за геометрической асимметрии реальных объектов гидравлические свойства могут зависеть от направления. Однако, в силу малости противотоков, будем считать, что проницаемость одинакова во всех направлениях как для цилиндрической, так и для плоской стенки фильтра.

Слайд 29Рис. 25. Протокол работы программы регрессионного анализа
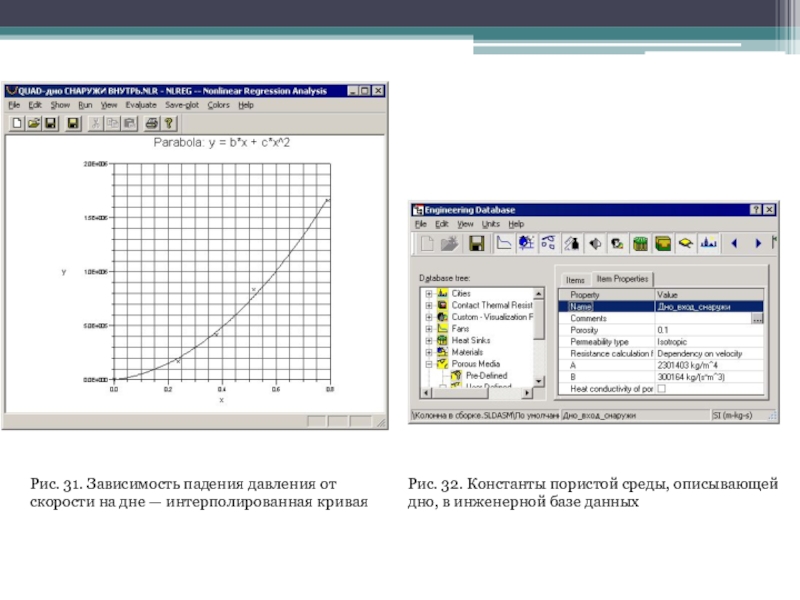
Слайд 30Рис. 26. Зависимость падения давления от скорости — интерполированная кривая
Слайд 31Рис. 27. Константы пористой среды, описывающей боковые стенки
в инженерной базе
данных
Слайд 32Следующий этап — получение констант условной пористой среды, имитирующей донную
часть фильтра. Соответствующая геометрическая модель с граничными условиями (для входа,
как и в случае цилиндрической стенки, назначаются несколько значений давления) показана на рис. 28. Фрагмент геометрии приведен на рис. 29. Как видно, модель содержит дефект: присутствует интерференция фильтрующих ребер и ребер несущих. Тем не менее, для гидравлического расчета, не предусматривающего учет теплопроводности в телах, корректировка не требуется: модуль Flow Simulation обрабатывает такие ситуации вполне корректно.
Рис. 28. Граничные условия для модели дна
Рис. 29. Геометрия фильтра в расчетной модели течения через дно
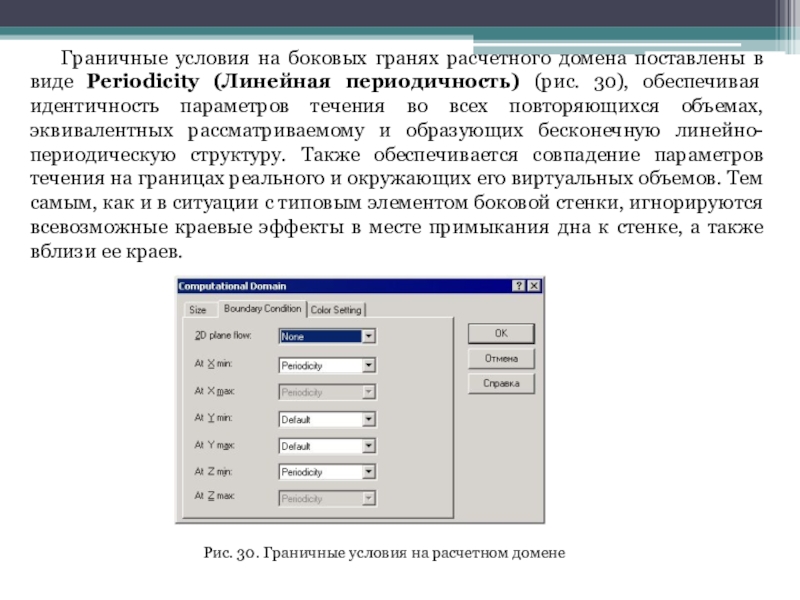
Слайд 33Граничные условия на боковых гранях расчетного домена поставлены в виде
Periodicity (Линейная периодичность) (рис. 30), обеспечивая идентичность параметров течения во
всех повторяющихся объемах, эквивалентных рассматриваемому и образующих бесконечную линейно-периодическую структуру. Также обеспечивается совпадение параметров течения на границах реального и окружающих его виртуальных объемов. Тем самым, как и в ситуации с типовым элементом боковой стенки, игнорируются всевозможные краевые эффекты в месте примыкания дна к стенке, а также вблизи ее краев.
Рис. 30. Граничные условия на расчетном домене
Слайд 34Остальные манипуляции, необходимые для получения зависимости между падением давления при
прохождении текучей среды через плоский фильтр и скоростью на удалении
от него, эквивалентны описанным для цилиндрических стенок. В данном случае из-за постоянства проходного сечения однозначным является вопрос о том, какую скорость следует принимать в качестве аргумента функции. Вне возмущенной зоны это есть средняя скорость течения в произвольном сечении, в частности на входе или выходе. Результат подбора параболической функции с нанесенными на нее "экспериментальными" точками выглядит, как показано на рис. 31, а собственно константы приведенной пористой среды приведены на рис. 32. Как видно, они существенно отличаются от рассчитанных для среды, имитирующей боковые стенки.
Слайд 35Рис. 31. Зависимость падения давления от скорости на дне —
интерполированная кривая
Рис. 32. Константы пористой среды, описывающей дно, в инженерной
базе данных
Слайд 36Интересно сравнить модели течения с реальным фильтром и с его
виртуальной моделью (с рассчитанными характеристиками пористой среды). Условия задачи, в
частности факт присвоения специально созданному телу свойств изотопной пористой среды, показаны на рис. 33. Подчеркнем, что толщина тела принята равной условной толщине фильтрующего объекта (см. рис. 19), то есть 7 мм.
Как видно, граничные условия заимствованы из модели с "реальным" фильтром.
Расчетная сетка показана на рис. 34: она имеет те же базовые параметры, что и ранее, но на самом фильтре уплотнение незначительно.
Рис. 33. Граничные условия в модели с виртуальной пористой средой
Рис. 34. Расчетная сетка в модели с виртуальной пористой средой
Слайд 37Диаграмма скорости в сечении плоскостью, перпендикулярной оси, показана на рис.
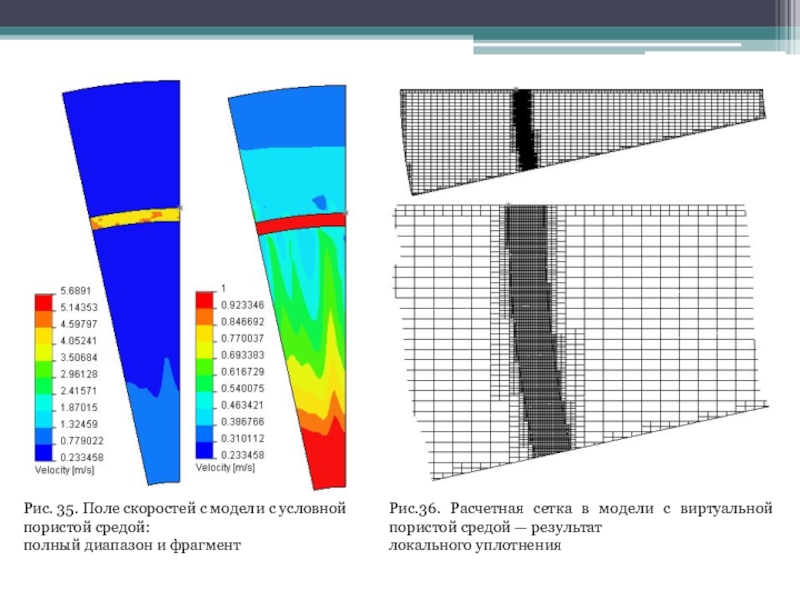
35. Очевидно, что имеет место существенная неоднородность потока, нивелирующаяся на
расстоянии более 10 толщин фильтра. В принципе, не рекомендуется значительно уплотнять сетку на объектах с виртуальной пористой средой. Тем не менее попробуем это сделать. Расчетная сетка и ее фрагмент показаны на рис. 36, а поле скорости во всем ее диапазоне, а также после снижения верхней границы диапазона, показано на рис. 37. Как видно, проблема флуктуаций в окружном направлении снята, и скорость на равном расстоянии от оси практически постоянна.
Распределение давления в сечении показано на рис. 38, а графики изменения давления и скорости вдоль радиуса — на рис. 39, 40. Можно убедиться, что проблема негомогенности течения снята, а графики вполне соответствуют полученным для модели с учетом "тонкой" структуры. Само собой, отсутствует локальный спад давления в месте ускорения потока через узкий канал по причине отсутствия такового в идеализированной модели. Величины падения давления и скачка скорости в обеих моделях вполне сопоставимы. Таким образом, получено косвенное подтверждение пригодности эффективных характеристик для исследования сложных систем с фильтрами, а также приняты рекомендации о необходимости (возможности) уплотнения сетки в "фильтрующем" теле и на его границах.

Слайд 38Рис. 35. Поле скоростей с модели с условной пористой средой:
полный
диапазон и фрагмент
Рис.36. Расчетная сетка в модели с виртуальной пористой
средой — результат
локального уплотнения
Слайд 39Рис. 37. Поле скоростей в модели
с условной пористой средой
Рис.38. Распределение
давления
в модели с условной пористой средой
Слайд 40Рис. 39. Давление вдоль отрезка в модели с условной пористой
средой
Рис.40. Скорость вдоль отрезка в модели с условной пористой средой
Слайд 41Расчет течения в колонне
Расчетный домен и граничные условия на фоне
вида с разрезом фильтрующей колонны показаны на рис. 41. Как
видно, условие на единственном входе — массовый расход, а на единственном же выходе — давление окружающей среды. Имея в виду именно эти условия, формировалась геометрия модели. Заглушка на входном патрубке отстоит от его открытой части примерно на два диаметра, а на выходе — на три. Это является минимально необходимым расстоянием. Более того, прямой участок на выходе можно было сделать и длиннее, однако, как показал расчет, диагностических сообщений о вихрях, пересекающих границу с назначенным давлением, не появилось.
Несмотря на наличествующую геометрическую симметрию относительно вертикальной плоскости XY (плоскость разреза на иллюстрации совпадает с ней), симметрия течения не гарантируется. Поэтому в расчете участвует полная модель.
В геометрическую модель введены две детали: одна охватывает фильтры и выходной патрубок, вторая конец входного патрубка и часть рассекателя. Они послужат для назначения параметров локальной начальной сетки. Чтобы соответствующие тела стали прозрачными для текучей среды, их следует отключить (деактивировать), что выполняем в окне Component Control (Управление деталями) (рис. 42).

Слайд 42Боковым стенкам фильтров (им соответствуют тела в детали), выходящим в
нижний объем колонны, а также деталям, описывающим днища, присваиваем характеристики
гомогенных пористых сред, рассчитанные ранее (рис. 43). Соответствующая команда подается из Дерева проекта Flow Simulation (рис. 44).
Рис. 41. Граничные условия для течения в колонне
Рис. 42. Отключение деталей, прозрачных для текучей среды
Слайд 43Рис. 44. Присвоение характеристик пористых сред объектам в модели
Рис. 43.
Пористые среды в модели
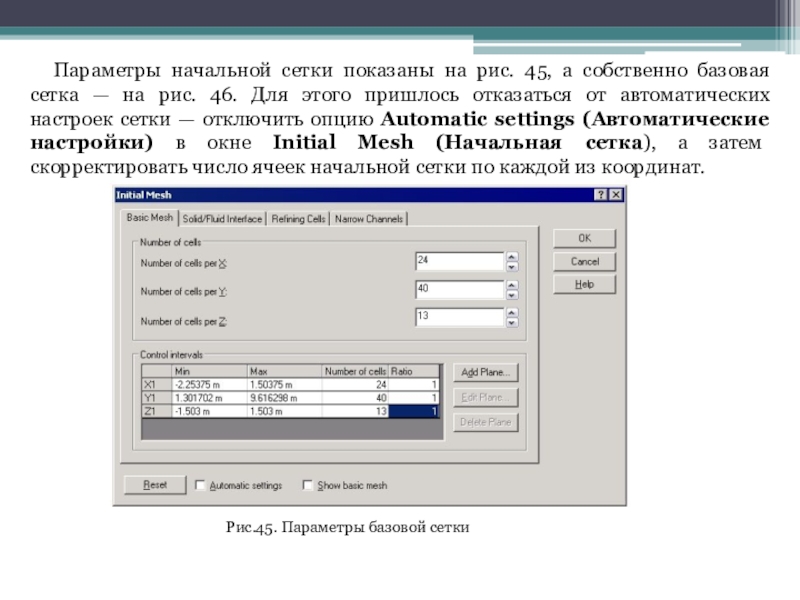
Слайд 44Параметры начальной сетки показаны на рис. 45, а собственно базовая
сетка — на рис. 46. Для этого пришлось отказаться от
автоматических настроек сетки — отключить опцию Automatic settings (Автоматические настройки) в окне Initial Mesh (Начальная сетка), а затем скорректировать число ячеек начальной сетки по каждой из координат.
Рис.45. Параметры базовой сетки
Слайд 45Рис.46. Начальная сетка в вертикальных сечениях
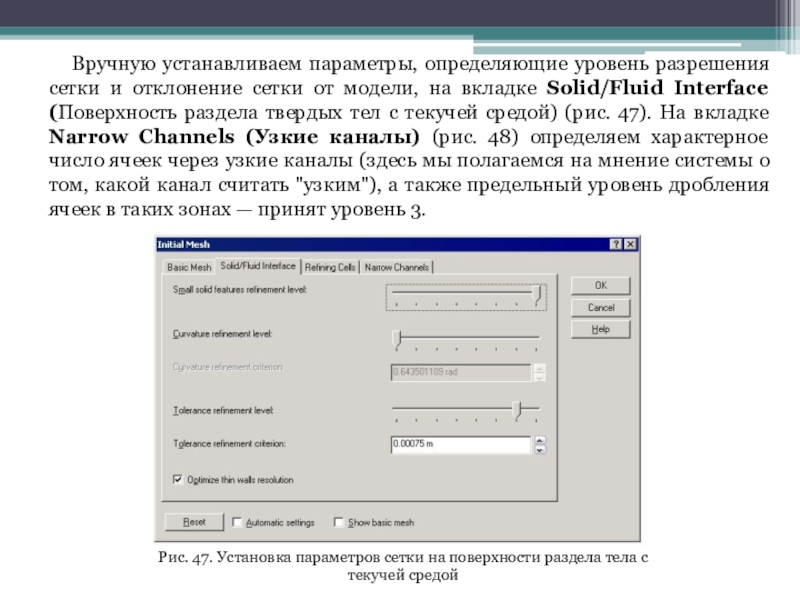
Слайд 46Вручную устанавливаем параметры, определяющие уровень разрешения сетки и отклонение сетки
от модели, на вкладке Solid/Fluid Interface (Поверхность раздела твердых тел
с текучей средой) (рис. 47). На вкладке Narrow Channels (Узкие каналы) (рис. 48) определяем характерное число ячеек через узкие каналы (здесь мы полагаемся на мнение системы о том, какой канал считать "узким"), а также предельный уровень дробления ячеек в таких зонах — принят уровень 3.
Рис. 47. Установка параметров сетки на поверхности раздела тела с текучей средой
Слайд 47Рис. 48. Параметры сетки при обработке узких каналов
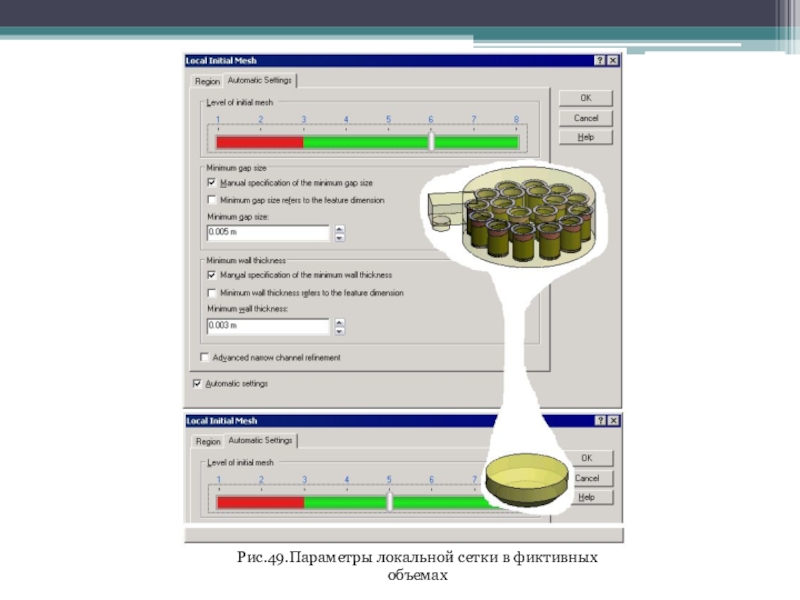
Слайд 48Уплотнять сетку в фиктивных объемах будем посредством функции Local Initial
Mesh (Локальная начальная сетка). Окна, определяющие сетку в окрестности фильтров
и в зоне впуска, показаны на рис. 49. Как видно, здесь для зон фильтра и выхода назначен уровень дробления 6, а для зоны входа — 5. Это значит, что дробиться будут все ячейки, полностью или частично попавшие в указанные детали (тела).
Начальная сетка в вертикальных сечениях после генерации ее системой показана на рис. 50. Как видно, уплотнение в зоне фильтров выражено в большей степени, чем в нижней части бака. Высокая степень уплотнения в окрестности днищ фильтров объясняется действием ребер жесткости, которые не попали в аппроксимацию телами с пористой средой и распознаются системой как тонкие стенки и/или мелкие особенности геометрии. Также достаточно удовлетворительное качество сетки достигнуто в зоне выходного патрубка и смежных с ним объемов. В то же время между концом впускной трубы и рассекателем плотность сетки может оказаться недостаточной. Здесь проходное сечение аппроксимируется 5−6 ячейками. На этот факт реагируем следующим образом. Во-первых, в данном случае для нас в первую очередь интересна "интегральная" точность модели течения в этой зоне, поскольку первоочередными объектами исследования являются фильтры и их окрестности. С другой стороны, будет предпринята попытка адаптации сетки непосредственно в ходе расчета.

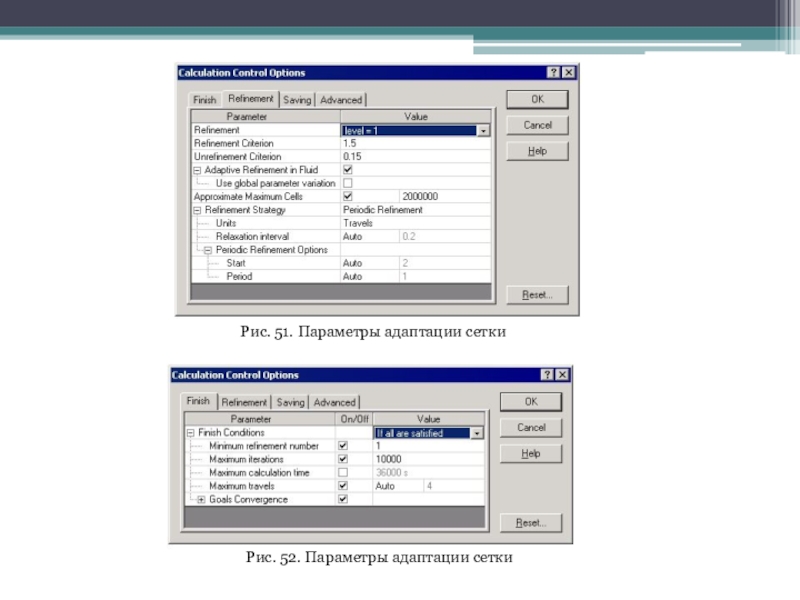
Слайд 49Для этого на вкладке Refinement (Адаптация сетки) окна Calculation Control
Options(Опции управления расчетом) в одноименном поле из выпадающего списка выбирается
уровень 1, назначается максимально возможное число ячеек (исходя прежде всего из соображений доступности оперативной памяти) (рис. 51). Также на вкладке Finish (Завершение) определяется, что расчет завершится только при удовлетворении всех условий с минимальным числом адаптаций — 1. Также (в данном случае это совсем необязательно, поскольку задача не относится к числу тех, где решение о завершении перекладывается на пользователя) устанавливается достаточно большое число итераций, чтобы расчет можно было продолжить без каких-либо дополнительных манипуляций (рис. 52), а также быть уверенным, что останов не случится "не вовремя".
Кстати говоря, весь этот набор функций доступен и во время расчета из меню Calculation (Расчет) диалогового окна Solver (Решатель).
В качестве целей проекта назначаем статическое и динамическое давление на входе (цель на поверхности), а также среднюю и максимальную скорость в пределах всего объема текучей среды (глобальная цель). Тем самым мы декларируем желание добиться адекватной точности во всем объеме среды.

Слайд 50Рис.49.Параметры локальной сетки в фиктивных объемах
Слайд 51Рис. 50. Начальная сетка в вертикальных сечениях
Слайд 52Рис. 51. Параметры адаптации сетки
Рис. 52. Параметры адаптации сетки
Слайд 53Сетка (ее сечение) после одного шага адаптации показана на рис.
53. Как видно, она изрядно отличается от базовой сетки.
Диаграмма скорости
в вертикальном сечении, проходящем через патрубки, показана на рис. 54. Как видно, максимальная скорость 3,32 м/c (она имеет место на входе) достаточно велика в сравнении со средней по объему. Поэтому ту же диаграмму показываем с ограничением верхней границы шкалы до 0,1 м/c. Результат показан на рис. 55. Как видно, изображение приобрело достаточную наглядность. Обращает на себя внимание достаточно малая, по сравнению с "основным" объемом бака, скорость движения через фильтры.
Статическое давление в сечении показано на рис. 59. При этом диапазон для шкалы был адаптирован (сужен) так, чтобы повысить контрастность в области возле фильтров. Также посредством процедуры Probe (Проба) выделено значение функции в двух парах точек: до и после фильтров, расположенных ближе к выходу и дальше от него. Как видно, на левом фильтре падение давления составляет около 5 Па, а на втором — несколько меньше, около 3 Па.
Слайд 54Рис. 53. Сетка после одного
шага адаптации
Рис. 54. Поле скоростей в
сечении
вертикальной плоскостью,
проходящей через патрубки
Рис.55. Поле скоростей в сечении
плоскостью, проходящей через
патрубки —
обрезанный диапазон
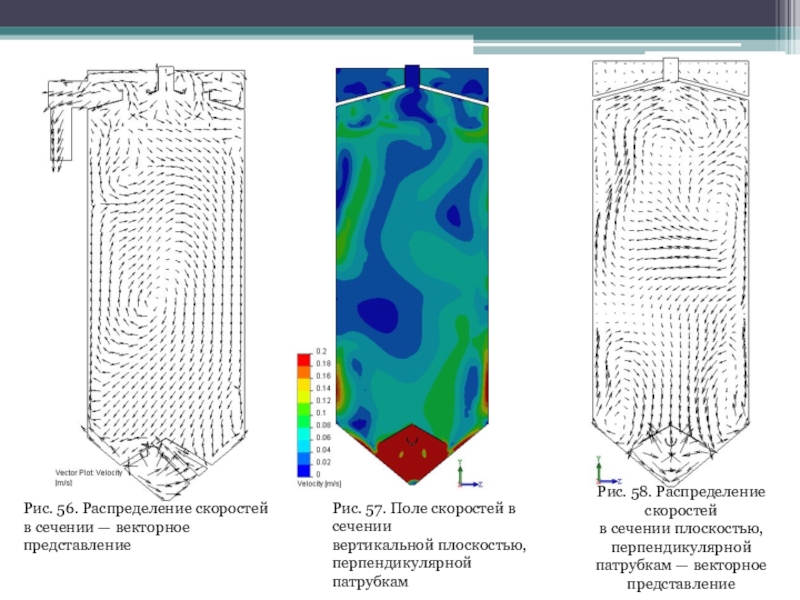
Слайд 55Рис. 56. Распределение скоростей
в сечении — векторное представление
Рис. 57. Поле
скоростей в сечении
вертикальной плоскостью,
перпендикулярной патрубкам
Рис. 58. Распределение скоростей
в сечении плоскостью,
перпендикулярной
патрубкам — векторное представление
Слайд 56Рис. 59. Распределение статического давления в сечении плоскостью, проходящей через
патрубки — обрезанный диапазон
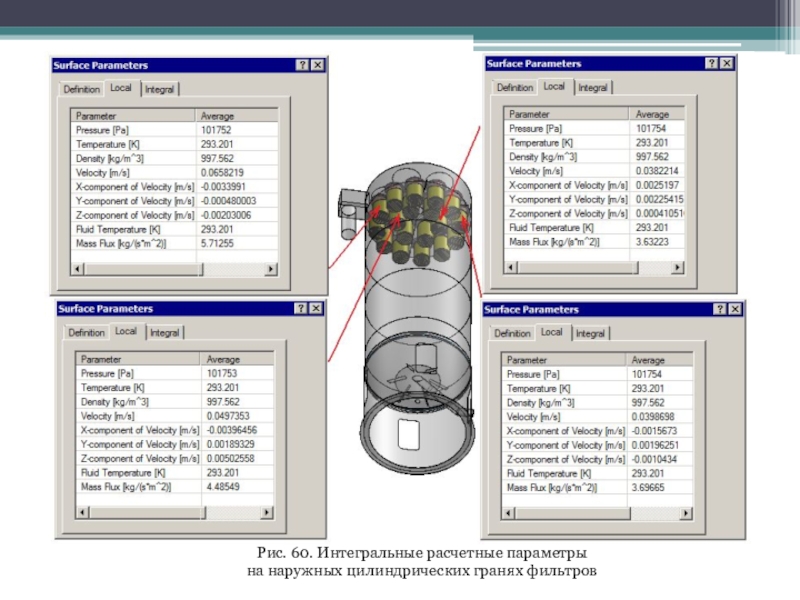
Слайд 57Более детализированную и точную информацию можно получить посредством процедуры Surface
Parameters (Параметры на поверхности). Например, если применить ее к наружным
цилиндрическим граням фильтров, расположенным вдоль плоскости симметрии, то результаты будут выглядеть, как показано на рис. 60. Как видно, средний массовый расход варьируется от 5,7 до 3,6 кг/м2 в секунду. Надо полагать, что фильтры на периферии могут иметь еще меньшую интенсивность фильтрации. Таким образом, можно оценить степень равномерности при загруженности фильтров.
На рис. 61 аналогичная по структуре информация собрана для внутренней и наружной граней дна фильтра, ближайшего к выходу. Как видно, падение давления составляет около 5 Па, а скорость в направлении оси Y (перпендикулярно фильтру) снаружи — 0,017 м/с и внутри — 0,021 м/c. Причина того, что скорости, как, кстати, и массовые расходы, неодинаковы в том, что изнутри к фильтру (телу, его заменяющему) примыкают ребра, через которые не происходит движения текучей среды.
Слайд 58Рис. 60. Интегральные расчетные параметры
на наружных цилиндрических гранях фильтров
Слайд 59В контексте данной задачи актуальной становится одна из относительно редко
используемых процедур Flow Simulation — расчет среднего времени прохождения средой
расстояния от входа до какой-либо точки Dimensionless LMA (Local Мean Аge) и местного значения коэффициента воздухообмена LACI (Local Air Change Index). Последняя характеристика рассчитывается как V/Q, где V — объем расчетной области, а Q — отношение объемного расхода на входе (входах) к среднему времени, необходимому для прохождения текучей средой расстояния от входа до какой-либо точки.
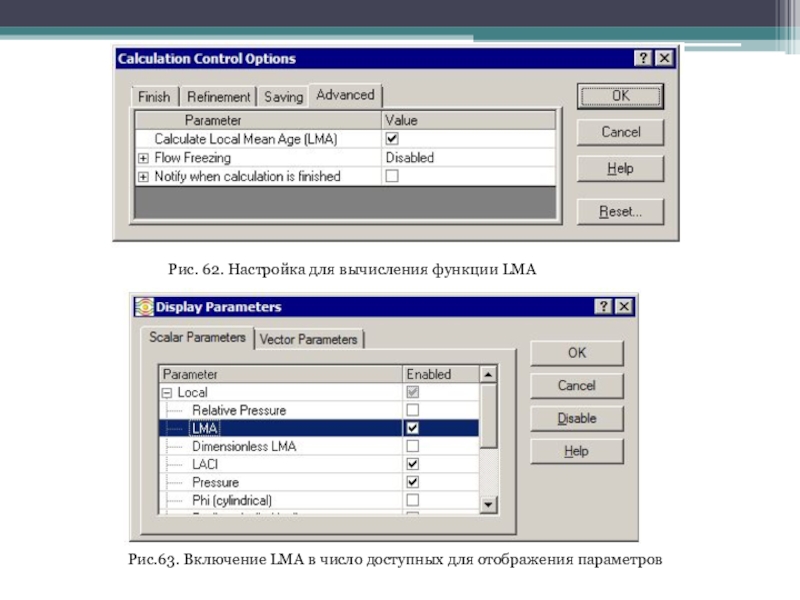
Здесь следует отметить, что по умолчанию Flow Simulation может иметь настройки, при которых в процессе выполнения расчета параметры LMA не вычисляются. Соответствующий регулятор находится на вкладке Advanced (Дополнительные параметры) окна Calculation Control Options (Опции управления расчетом) (рис. 62). Перед расчетом нужно активизировать опцию LMA.
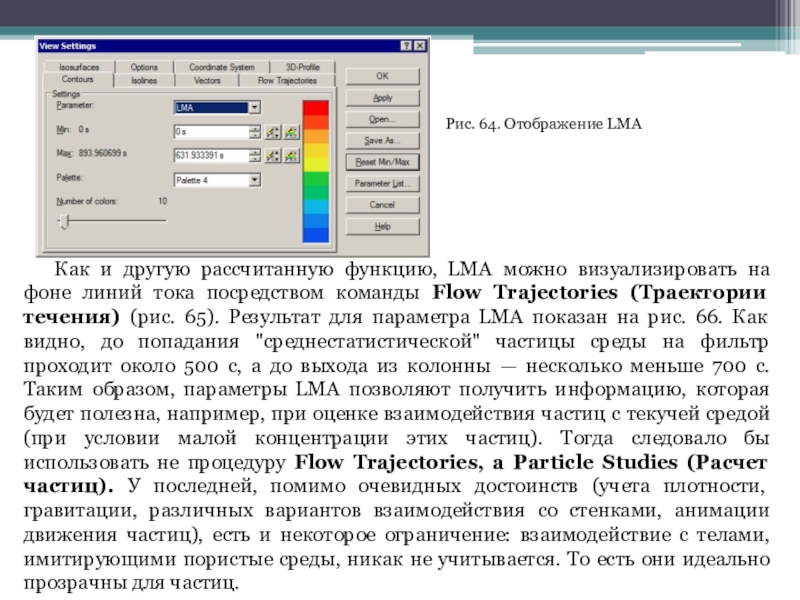
После выполнения расчета при попытке отобразить параметры из группы LMA можно потерпеть неудачу. Дело в том, что они не входят в число параметров, визуализируемых по умолчанию. Поэтому при попытке создать подобную диаграмму нужно подать команду View Settings (Установки просмотра), затем в одноименном окне нажать кнопку Parameter List (Список параметров) и в окне Display Parameters (Параметры визуализации) включить опцию LMA (рис. 63, 64).

Слайд 60Рис. 61. Интегральные параметры на внутренней и наружной гранях дна
Слайд 61Рис. 62. Настройка для вычисления функции LМА
Рис.63. Включение LMA в
число доступных для отображения параметров
Слайд 62Рис. 64. Отображение LMA
Как и другую рассчитанную функцию, LMA можно
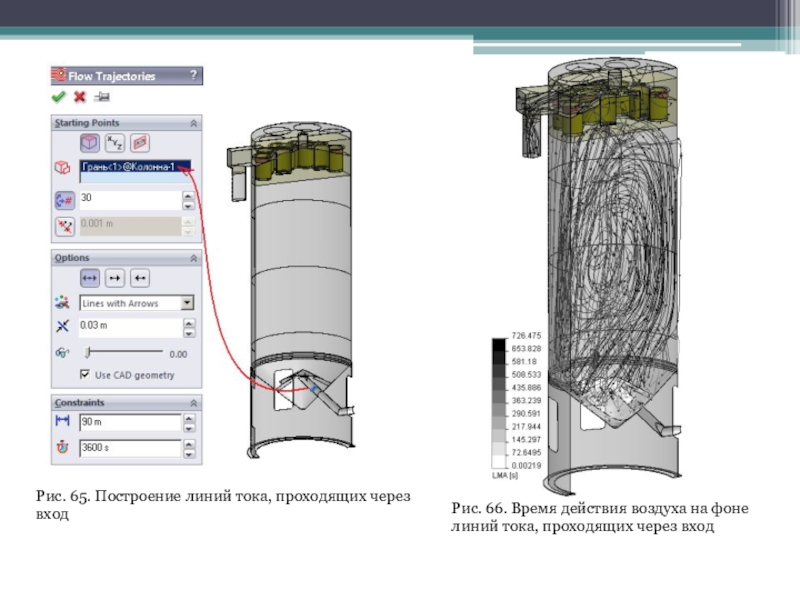
визуализировать на фоне линий тока посредством команды Flow Trajectories (Траектории
течения) (рис. 65). Результат для параметра LMA показан на рис. 66. Как видно, до попадания "среднестатистической" частицы среды на фильтр проходит около 500 с, а до выхода из колонны — несколько меньше 700 с. Таким образом, параметры LMA позволяют получить информацию, которая будет полезна, например, при оценке взаимодействия частиц с текучей средой (при условии малой концентрации этих частиц). Тогда следовало бы использовать не процедуру Flow Trajectories, а Particle Studies (Расчет частиц). У последней, помимо очевидных достоинств (учета плотности, гравитации, различных вариантов взаимодействия со стенками, анимации движения частиц), есть и некоторое ограничение: взаимодействие с телами, имитирующими пористые среды, никак не учитывается. То есть они идеально прозрачны для частиц.
Слайд 63Рис. 65. Построение линий тока, проходящих через вход
Рис. 66. Время
действия воздуха на фоне линий тока, проходящих через вход
Слайд 64Выводы
Моделирование фильтрующих систем посредством SolidWorks Flow Simulation может быть выполнено
с различной степенью подробности. Для фильтра сложной структуры рациональным является
его замена пористой средой, параметры которой также могут быть рассчитаны с помощью виртуальной модели. В этом случае потребуется привлечение дополнительных математических инструментов, позволяющих рассчитать константы параболической функции, описывающей зависимость градиента давления от скорости при прохождении жидкостью (газом) условной пористой среды. На результат оказывает влияние направление движения текучей среды, особенности конструкции в месте расположения фильтрующих элементов.
Слайд 65ВОПРОСЫ ПО ЛЕКЦИИ
Из чего состоит фильтрующая колонна?
Какие типы пористых
сред содержит COSMOSFloWorks?
k = Δp×S (m× L) что
означают параметры в формуле?
Что представляет диаграмма скорости в сечении, перпендикулярном оси и проходящем посередине между витками(рис.23)
С помощью какой программы решается задача подбора коэффициентов А и B в зависимости: grad( p) =A×v2 +B×v?
Какие две детали в геометрическую модель при расчете течение в колонне?
Что назначается в качестве целей проекта при расчете течение в колонне?
Какие выводы можно сделать из рис. 61?
Какой параметр позволяет вычислять функция LMA?
Слайд 66Перечень учебно-методического обеспечения самостоятельной работы обучающихся по дисциплине
Алямовский, Андрей Александрович.
Инженерные расчеты в SolidWorks Simulation [Электронный ресурс] / А. А.
Алямовский. - Электрон. текстовые дан. - Москва : ДМК Пресс, 2010. - 464 с. - (Проектирование). - Режим доступа: http://e.lanbook.com/books/element.php?pl1_id=1319. - ISBN 978-5-94074-586-0 : Б. ц.
Алямовский, Андрей Александрович. COSMOSWorks. Основы расчета конструкций на прочность в среде SolidWorks [Электронный ресурс] / А. А. Алямовский. - Электрон. текстовые дан. - Москва : ДМК Пресс, 2010. - 784 с. : ил. - (Проектирование). - Режим доступа: http://e.lanbook.com/books/element.php?pl1_id=1318. - ISBN 978-5-94074-582-2 : Б. ц.
Перечень ресурсов информационно-телекоммуникационной сети «Интернет»
https://www.youtube.com/watch?v=R62pq1Oh92s
https://www.solidworks.com/ru










































![Лекция Перечень учебно-методического обеспечения самостоятельной работы обучающихся по дисциплинеАлямовский, Андрей Александрович. Инженерные Перечень учебно-методического обеспечения самостоятельной работы обучающихся по дисциплинеАлямовский, Андрей Александрович. Инженерные расчеты в SolidWorks Simulation [Электронный ресурс]](/img/tmb/6/582505/1abe5c0378f23d300c8ae6a77c6a4a26-800x.jpg)