Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
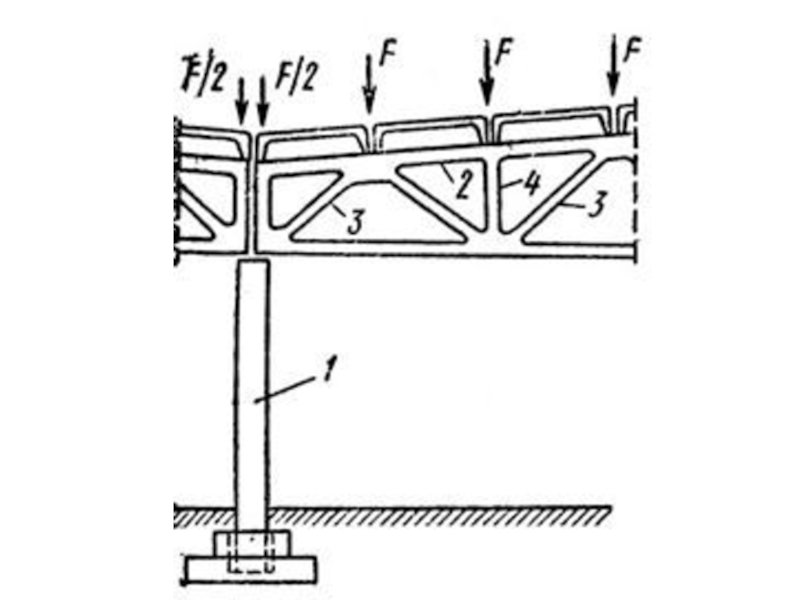
Задача 1. Проверить прочность центрально-растянутой подвески по ее ослабленному
Содержание
- 1. Задача 1. Проверить прочность центрально-растянутой подвески по ее ослабленному
- 2. Задача 2. Подобрать сечение затяжки арки, из
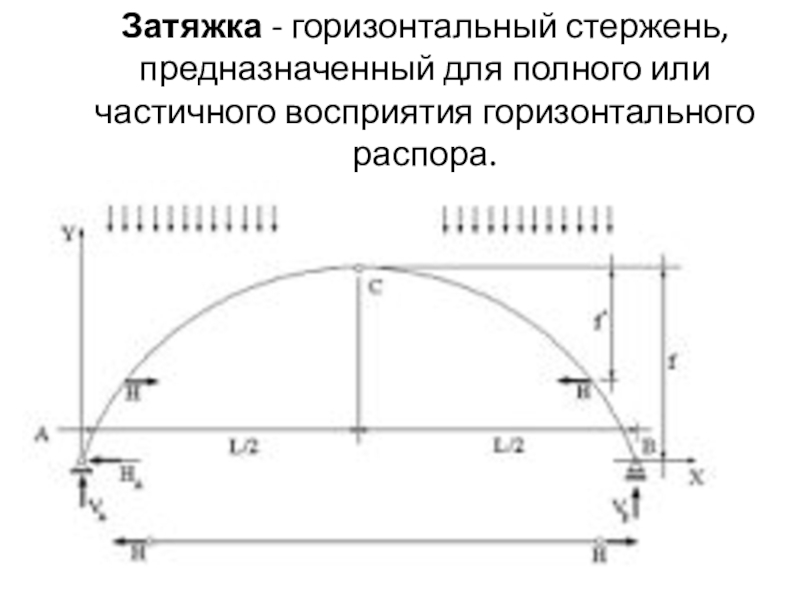
- 3. Затяжка - горизонтальный стержень, предназначенный для полного или частичного восприятия горизонтального распора.
- 4. Опр. Расчетное сопротивление стали по пред. ТекучестиКоэфф.
- 5. Задача 3. Подобрать сечение нижнего пояса фермы.
- 6. Опр. Расчетное сопротивление стали по пред. ТекучестиКоэфф.
- 7. Расчет центрально-сжатых элементовСжатые элементы бывают центрально-сжатыми и
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. 5.1. Расчет на прочность элементов, подверженных центральному растяжению
- 13. П. 5. 3 формула (7) (п 7)Расчет
- 14. ϕ см. СП п 5.3.Условная гибкость λ-
- 15. В сжатых конструкциях следует ограничивать гибкость λГибкость
- 16. Расчет центрально-сжатых элементовЗадача.1.Подобрать стержень основной колонны общественного
- 17. 1. Опр. Расчетное сопротивление стали по пределу
- 18. 4. Проверка подобранного сечения4.1. опред. Наибольшую фактическую
- 19. 4.4. Фактическое значение коэфф. устойчивости Д1. или формула4.5. Проверяем общую устойчивость5. Вывод
- 20. Задача 2. Подобрать сечение центрально-сжатого стержня решетки
- 21. 1. Расчетное сопротивление стали по пред.текучести, коэфф.
- 22. Скачать презентанцию
Задача 2. Подобрать сечение затяжки арки, из двух равнополочных уголков. Сталь С245. . Растягивающая сила N= 250 кН, γn= 1. Расчетные длины lefх = 9 м, lefу = 1,5 м. Предельная
Слайды и текст этой презентации
Слайд 1Задача 1.
Проверить прочность центрально-растянутой подвески по ее ослабленному сечению. Растягивающая
Слайд 2Задача 2.
Подобрать сечение затяжки арки, из двух равнополочных уголков.
Сталь С245. . Растягивающая сила N= 250 кН, γn= 1.
Расчетные длины lefх = 9 м, lefу = 1,5 м.
Предельная гибкость λпред = 400
Слайд 3Затяжка - горизонтальный стержень, предназначенный для полного или частичного восприятия горизонтального
распора.
Слайд 4Опр. Расчетное сопротивление стали по пред. Текучести
Коэфф. условия работы
Площадь нетто
Радиус инерции
Проверяем гибкость затяжки
Проверяем прочность по условию
вывод
Слайд 5Задача 3.
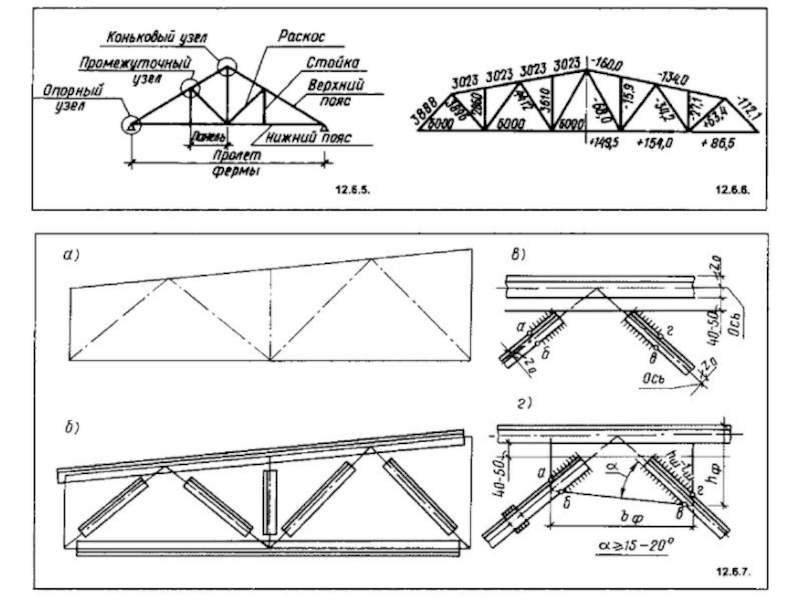
Подобрать сечение нижнего пояса фермы. Стержень выполнен из двух
равнополочных уголков, которые прикреплены к фасонкам t=10мм. Сталь С245. Растягивающая
сила N= 450 кН, γn= 0,95 . Расчетные длины lefх = 3 м, lefу1 = 6 м. Расстояние между краями фасонок Lн=2550ммСлайд 6Опр. Расчетное сопротивление стали по пред. Текучести
Коэфф. условия работы
Определяем требуем.
Площадь сечения. Площадь брутто (А) = площади нетто (А n)
Поверяем
гибкостьПроверяем прочность
Назначаем расстояние между соединительными прокладками.
Для растянутых стерней не более 80*iх
7.Вывод
Слайд 7Расчет центрально-сжатых элементов
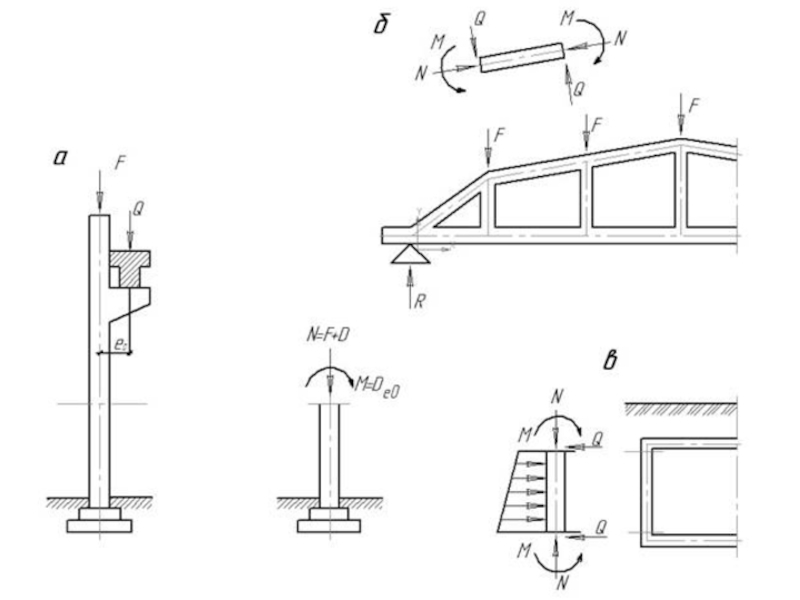
Сжатые элементы бывают центрально-сжатыми и внецентрально сжатыми.
К центрально-сжатым
относят :
некоторые симметрично загруженные колонны, стойки, элементы стропильных ферм
Слайд 125.1. Расчет на прочность элементов, подверженных центральному растяжению или сжатию силой ,
кроме указанных в п.5.2, следует выполнять по формуле (5)
Ϭ =
N/ An ≤ Ry γ cПроверка прочности, если конструкция имеет ослабление (отверстие, выемки), которые уменьшают сечение, если их нет, проводить расчет общей устойчивости
Слайд 13П. 5. 3 формула (7) (п 7)
Расчет общей устойчивости :
Ϭ
= N/ ϕA ≤ Ryγc
ϕ - коэфф. устойчивости, в зависимости
от гибкости рассчитываемого элементаА - площадь сечения брутто
Слайд 14ϕ см. СП п 5.3.
Условная гибкость λ- = λ√Ry/Е
см
п.8.8 ниже
λ – гибкость элемента
Е – модуль упругости стали
Е=2,06*105МПа
Ry
– расчетное сопротивление стали, взятое пределу текучестиСлайд 15В сжатых конструкциях следует ограничивать гибкость λ
Гибкость проверяют по формуле
λ = lef / i ≤ λпред
Предельные гибкости сжатых
элементов т. 19 , п.6.15
Расчетные длины для колонн опред. По формуле
lef = μl
Для стержней ферм, т. 11 п. 6.1
Слайд 16Расчет центрально-сжатых элементов
Задача.1.
Подобрать стержень основной колонны общественного здания. Стержень колонны
выполнен из прокатного двутавра с параллельными гранями потолок. Нагрузка N=400кН,
γn= . Длина колонны l=2,8 м. Расчетная схема колонны и ее сечение см.рис.Слайд 171. Опр. Расчетное сопротивление стали по пределу текучести
2. Расчет
прочности не производим. Рассчитываем колонну на общую устойчивость.
2.1. Коэфф. γn
и ϕ2.2. Определяем А
3. По требуемой площади (А)подбираем двутавр
Слайд 184. Проверка подобранного сечения
4.1. опред. Наибольшую фактическую гибкость
Наибольшая гибкость
будет относительно оси у , так как радиус инерции относительно
оси у меньше радиуса инерции относительно оси х, а расчетные длины колонны относительно этих осей одинаковыеРасчетная длина колонны
4.2. Опред. Наибольшую гибкость
4.3.По наибольшей гибкости определяем условную гибкость
Слайд 194.4. Фактическое значение коэфф. устойчивости Д1. или формула
4.5. Проверяем общую
устойчивость
5. Вывод
Слайд 20Задача 2.
Подобрать сечение центрально-сжатого стержня решетки стальной стропильной фермы,
из двух уголков. На стержень действует усилие N=300кН, γn= 1.
Длина стержня (расстояние между узлами фермы ) l=3000мм, фасонка t=10мм, сталь С345.Слайд 211. Расчетное сопротивление стали по пред.текучести, коэфф. условия работы.
2. Расчетные
длины плоской фермы
Расчетная длина в плоскости, перпендикулярной плоскости фермы.
3.
Задаемся гибкостью , находим условную гибкость, коэфф. устойчивости ϕ4. Находим требуемую площадь сечения стержня (А)
5. Подбираем уголки
6. Опред. Фактическую гибкость стержня относительно осей х у
По большему значению гибкость опред. Условную гибкость, коэфф. устойчивости ϕ.
7. Проверяем общую устойчивость
8. Проверяем гибкость
Вывод