Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задача экономического содержания в ЕГЭ № 17 аннуитетный платеж
Содержание
- 1. Задача экономического содержания в ЕГЭ № 17 аннуитетный платеж
- 2. Критерии оценивания
- 3. Словарик:Аннуитетная схема – все платежи единого размера на протяжении всего периода выплат.Транш – платёж (перевод денег).
- 4. В первую очередь нужно уметь распознать тип
- 5. Что необходимо знать при решении задач на
- 6. Задачи, связанные с изменением величиныПусть So
- 7. Типы задач при аннуитетной схеме :Нахождение ежегодного
- 8. Слайд 8
- 9. Оформление задач при аннуитетной схеме
- 10. Слайд 10
- 11. Нахождение ежегодного платежа31 декабря 2013 года Сергей
- 12. 31 декабря 2014 года Дмитрий взял
- 13. Ответ: две выплаты по 2 622 050 рублей
- 14. 31 декабря 2014 года Владимир взял
- 15. Ответ: 7 490 000 рублей
- 16. Нахождение количества лет (месяцев) выплаты кредита1 июня
- 17. 1 января 2015 года Александр Сергеевич
- 18. Через два месяца: Через 3 месяца: После
- 19. 31 декабря 2014 года Евгений взял
- 20. Ответ: 12 %
- 21. В июле планируется взять кредит на сумму
- 22. Решение:Пусть x (рублей) - нужно платить ежегодно.1)
- 23. Решим это уравнение и найдем x.((9662400*1,2-1,2x
- 24. Пример №2В июле планируется взять кредит в
- 25. Решение:Пусть в банке было взято X млн.
- 26. 1,2*(1,2⋅(1,2X−2,16) −2,16)-2,16=01,23⋅X=7,8624X=4,55То есть в банке было взято 4,55 млн. руб. Ответ: 4,55
- 27. Пример № 3Клиент взял в банке в
- 28. А=4775400Х – сумма платежа клиента
- 29. Слайд 29
- 30. Решение:1)В конце первого года долг составит: 1500000
- 31. Задача № 531 декабря 2014 года Максим
- 32. Слайд 32
- 33. Слайд 33
- 34. Решение.1) В конце первого года долг составит:
- 35. . В банк помещена сумма 3
- 36. Вычисление процентной ставки по кредиту31 декабря 2013
- 37. Решение:
- 38. Скачать презентанцию
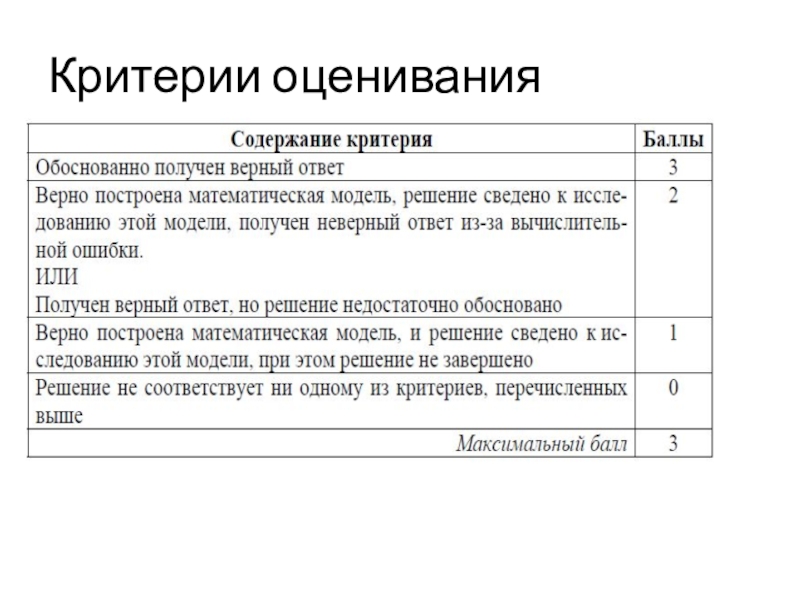
Критерии оценивания
Слайды и текст этой презентации
Слайд 4В первую очередь нужно уметь распознать тип задачи, прочитав условие
задачи.
Ключевая фраза при аннуитетной схеме платежа: долг выплачен равными платежами.
Слайд 5Что необходимо знать при решении задач на проценты:
1% от числа
А = 1/100 А
За 100% принимается та величина,
с которой сравнивают.3. Чтобы перевести проценты в десятичную дробь, необходимо количество процентов разделить на 100.
4. Если число Х увеличили на р%, то получим: Х(1 + 0,01р);
5. Если число Х уменьшили на р%, то получим: Х(1- 0,01р);
6. Если величину Х дважды увеличили на р%, получим: Х(1 + 0,01р)2;
7. Если величину Х дважды уменьшили на р%, получим: Х(1 – 0,01p)2
8. Если величину Х увеличили на р% n количество раз, то получим:
Х(1 + 0,01р) n;
9. Если величину Х сначала увеличили на р%, а затем уменьшили на к%, получим: Х(1+0,01р)(1-0,01k).
Слайд 6
Задачи, связанные с изменением величины
Пусть So – первоначальная величина,
S – новая величина.
Повышение на a%
n раз на a% S= So ·(1+0,01a) S= So ·(1+0,01a)n
Понижение на a% n раз на a%
S= So ·(1-0,01a) S= So ·(1-0,01a)n
Слайд 7Типы задач при аннуитетной схеме :
Нахождение ежегодного платежа.
Нахождение количества лет
выплаты кредита (начислений по вкладу).
Нахождение суммы кредита.
Вычисление процентной ставки по
кредиту.Слайд 11Нахождение ежегодного платежа
31 декабря 2013 года Сергей взял в банке
9 930 000 рублей в кредит под 10% годовых. Схема
выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определенную сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?Решение:
1,1(1,1 (1,1S – x) – х) – х = 0 S = 9 930 000
1,331S – 3,31х = 0
х = 3 993 000 Ответ: 3 993 000
Слайд 12 31 декабря 2014 года Дмитрий взял в банке 4 290
000 рублей в кредит под 14,5% годовых. Схема выплаты кредита
следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся часть долга (т.е. увеличивает долг на 14,5%), Затем Дмитрий переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Дмитрий выплатил платеж двумя равными платежами (т.е. за два года)?Слайд 14 31 декабря 2014 года Владимир взял в банке некоторую сумму
в кредит под 14% годовых. Схема выплаты кредита следующая: 31
декабря каждого следующего года банк начисляет проценты на оставшуюся часть долга (т.е. увеличивает долг на 14%), Затем Владимир переводит в банк 4 548 600 рублей. Какую сумму взял Владимир в банке, если он выплатил долг двумя равными платежами?Слайд 16Нахождение количества лет (месяцев) выплаты кредита
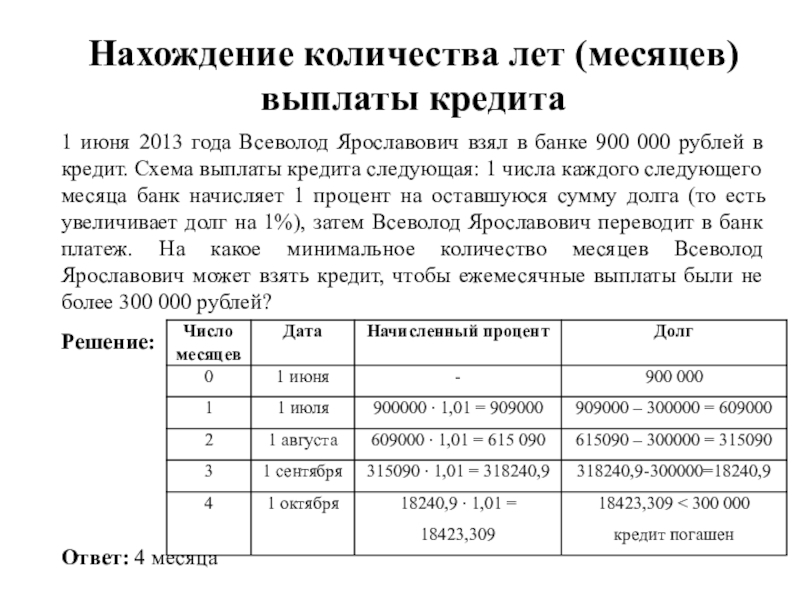
1 июня 2013 года Всеволод
Ярославович взял в банке 900 000 рублей в кредит. Схема
выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Всеволод Ярославович переводит в банк платеж. На какое минимальное количество месяцев Всеволод Ярославович может взять кредит, чтобы ежемесячные выплаты были не более 300 000 рублей?Решение:
Ответ: 4 месяца
Слайд 17 1 января 2015 года Александр Сергеевич взял в банке 1,1
млн. рублей в кредит. Схема выплаты кредита следующая – 1
числа каждого следующего месяца банк начисляет 1% на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Александр Сергеевич переводит в банк платеж. На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс. рублей?Слайд 18Через два месяца:
Через 3 месяца:
После погашения части долга
Х, остаток кредите составит:
Через 4:
Т.о. через n месяцев:
Ответ: 5
Слайд 19 31 декабря 2014 года Евгений взял в банке 1 млн.
рублей в кредит. Схема выплаты кредита следующая: 31 декабря каждого
следующего года банк начисляет проценты на оставшуюся часть долга (т.е. увеличивает долг на а%), Затем Евгений переводит в банк очередной транш. Евгений выплатил кредит за два транша, переведя в первый раз 540 тыс. рублей, а во второй 649,6 тыс. рублей. Под какой процент банк выдал кредит Евгению?Слайд 21В июле планируется взять кредит на сумму 8052000 рублей. Условия
его возврата таковы: - каждый январь долг возрастает на 20% по
сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить некоторую часть долга Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами (то есть за 4 года)?Слайд 22Решение:
Пусть x (рублей) - нужно платить ежегодно.
1) 1 год:
В январе
сумма долга составит 8052000*1,2 = 9662400.
После 1 платежа сумма долга
станет равна 9662400 - x.2) 2 год:
В январе сумма долга составит (9662400 - x)*1,2.
После 2 платежа сумма долга станет равна (9662400 - x)*1,2 - x.
3) 3 год:
В январе сумма долга составит ((9662400 - x)*1,2 - x)*1,2.
После выплаты сумма долга станет равна ((9662400 - x)*1,2 - x)*1,2 - x.
4) 4 год:
В январе сумма долга составит (((9662400 - x)*1,2 - x)*1,2 - x)*1,2.
После 4 платежа сумма долга станет равна (((9662400 - x)*1,2 - x)*1,2 - x)*1,2 - x.
Так как кредит был погашен 4 равными платежами, то после 4 платежа долга не осталось, т.е.
(((9662400 - x)*1,2 - x)*1,2 - x)*1,2 - x = 0.
Слайд 23
Решим это уравнение и найдем x.
((9662400*1,2-1,2x - x)*1,2 -
x)*1,2 - x = 0,
(9662400*1,22 - 2,64x-x)*1,2 - x = 0,
9662400*1,23 -
4,368x - x = 0,5,368x = 9662400*1,23,
x = 3 110 400.
Слайд 24Пример №2
В июле планируется взять кредит в банке на некоторую
сумму. Условия его возврата таковы: - каждый январь долг возрастает на
20% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить часть долга, равную 2,16 млн рублей. Сколько млн. рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами (то есть за 3 года)?Слайд 25Решение:
Пусть в банке было взято X млн. руб.
1) 1 год:
В
январе сумма долга будет составлять 1,2 X.
После 1 платежа сумма
долга составит: 1,2 X - 2,16.2) 2 год:
В январе сумма долга будет составлять 1,2⋅(1,2X−2,16)
После 2 платежа сумма долга составит: 1,2⋅(1,2X−2,16) −2,16
3) 3 год:
В январе сумма долга будет составлять 1,2*(1,2⋅(1,2X−2,16) −2,16)
После 3 платежа сумма долга составит: 1,2*(1,2⋅(1,2X−2,16) −2,16)-2,16
Так как кредит был погашен 3 равными платежами, то после 3 платежа долга не останется, т.е. станет равным 0.
Слайд 261,2*(1,2⋅(1,2X−2,16) −2,16)-2,16=0
1,23⋅X=7,8624
X=4,55
То есть в банке было взято 4,55 млн. руб.
Ответ:
4,55
Слайд 27Пример № 3
Клиент взял в банке в кредит 4775400 рублей
под 12% годовых на 18 месяцев, который намерен погасить тремя
равными платежами через 6 месяцев каждый. Схема выплаты кредита следующая: при поступлении платежа от клиента банк сначала начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 6% за прошедшие 6 месяцев), после чего списывает поступившую от клиента сумму. Какой должна быть сумма платежа клиента, если он погасил кредит тремя равными платежами?
Слайд 29
Пример №4
Максим хочет взять в банке кредит 1,5 миллиона рублей.
Погашение кредита происходит раз в год равными платежами (кроме, может быть, последней) после начисления процентов.
Процентная ставка- 10% годовых.
На какое минимальное количество лет может Максим взять кредит, чтобы ежегодные выплаты были не более 350 тысяч рублей?
Слайд 30Решение:
1)В конце первого года долг составит:
1500000 ∙ 1,1 –
350000 =1300000 (руб)
2) В конце второго года долг составит:
1300000 ∙ 1,1 – 350000 = 1080000 (руб)
3)В конце третьего года долг составит:
1080000 ∙ 1,1 – 350000 = 838000 (руб)
4)В конце четвертого года долг составит:
838000 ∙ 1,1 – 350000 = 571800 (руб)
5)В конце пятого года долг составит:
571800 ∙ 1,1 – 350000 = 278980 (руб)
6) В конце шестого года долг составит:
278900 ∙ 1,1 =306878 (руб)
Эта сумма менее 350000 руб.
Значит, кредит будет погашен за 6 лет.
Ответ: 6 лет
Слайд 31Задача № 5
31 декабря 2014 года Максим взял в банке
некоторую сумму денег в кредит под 10% годовых.
Схема выплаты
кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга, затем Михаил переводит в банк 2928200 рублей.
Какую сумму взял Михаил в банке,
если он выплатил долг четырьмя равными платежами, то есть за 4 года?
Слайд 32
Решение.
Пусть
x – сумма кредита.1)В конце первого года долг составит:
(1,1х – 2928200) рублей
2) В конце второго года долг (в рублях) составит:
(1,1х – 2928200)∙1,1 – 2928200 = 1,21х – 3221020 – 2928200 = 1,21х – 6149220
3) В конце третьего года долг (в рублях) составит:
(1,21х – 6149220)∙1,1 – 2928200 = 1,331х – 6764142 – 2928200 =1,331х – 9692342
4) В конце четвертого года долг (в рублях) составит 2928200 рублей:
(1,331х – 9692342)∙1,1 = 2928200;
1,4641х – 10661576 = 2928200;
1,4641х = 13589776;
х = 9281999,8. Значит, сумма кредита равна 9282000 рублей.
Ответ: 9282000 руб
Слайд 33
Задача №6.
31 декабря 2014 года Роман взял в банке 8599000 рублей в кредит под 14% годовых.
Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга
(то есть увеличивает долг на 14%), затем Роман переводит в банк Х рублей.
Какой должна быть сумма Х, чтобы Роман выплатил долг тремя равными платежами
(то есть за 3 года)?
Слайд 34Решение.
1) В конце первого года долг составит:
8599000∙1,14 – Х
= 9802860 – Х
2) В конце второго года долг
составит: (9802860 - Х)∙1,14 – Х=11175260 – 2,14∙Х
3) В конце третьего года долг (в рублях) составит:
(11175260 – 2,14∙Х) ∙1,14 – Х=12739796 – 3,4396∙Х.
Составим уравнение:
12739796 – 3,4396∙Х= 0
Х=3703860 рублей
Ответ: ежегодный транш составит 3703860 рублей.