Задачи на построение. 7 класс

Содержание

1. Задачи на построение. 7 класс
2. Задания на повторение1)Укажите, на каком из приведённых ниже рисунков имеются равные треугольники?
3. 2) В силу какого признака равенства треугольников
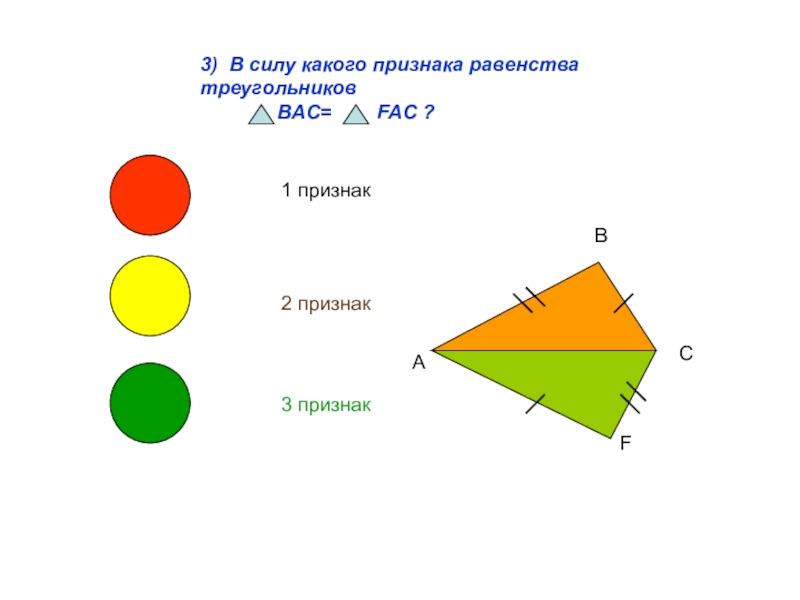
4. 3) В силу какого признака равенства треугольников
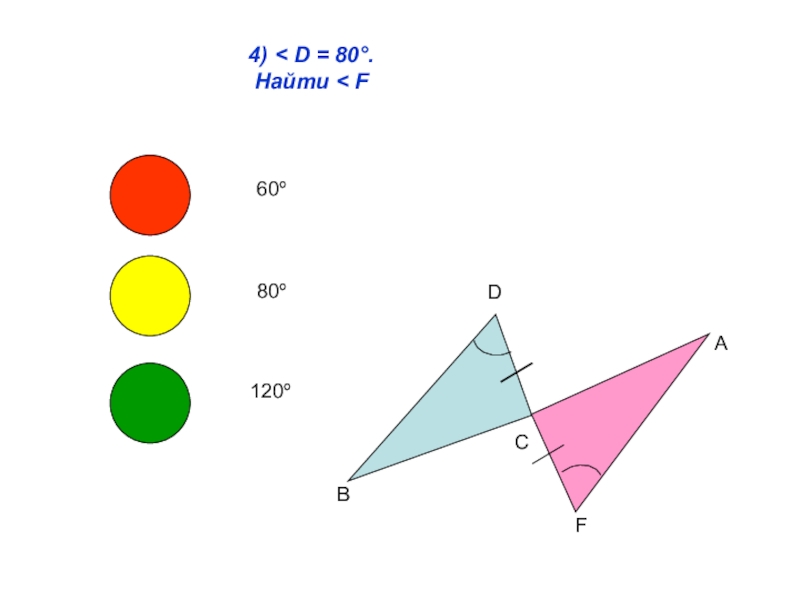
5. 4) < D = 80°. Найти < FDBCAF 60º80º120º
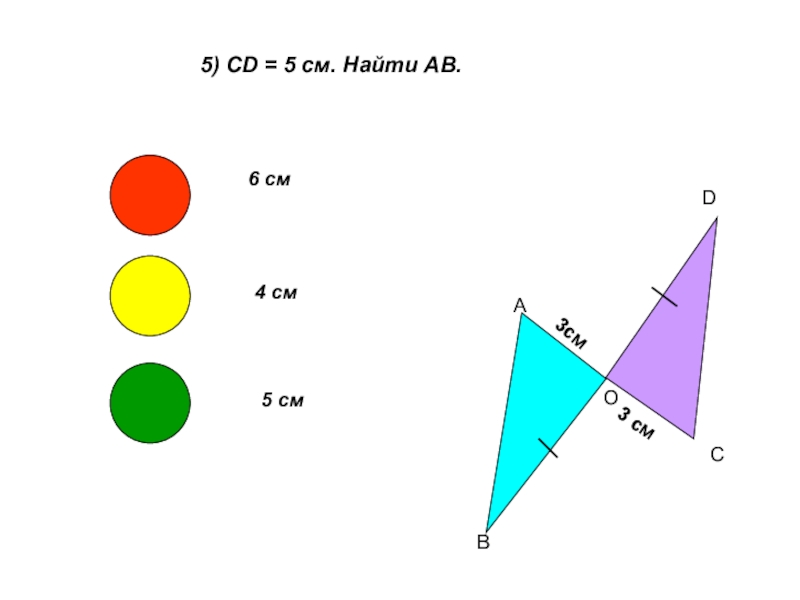
6. 5) CD = 5 см. Найти АВ.АВОDC3см3 см6 см4 см5 см
7. 6)Сколько медиан можно провести в треугольнике?ОднуДвеТри
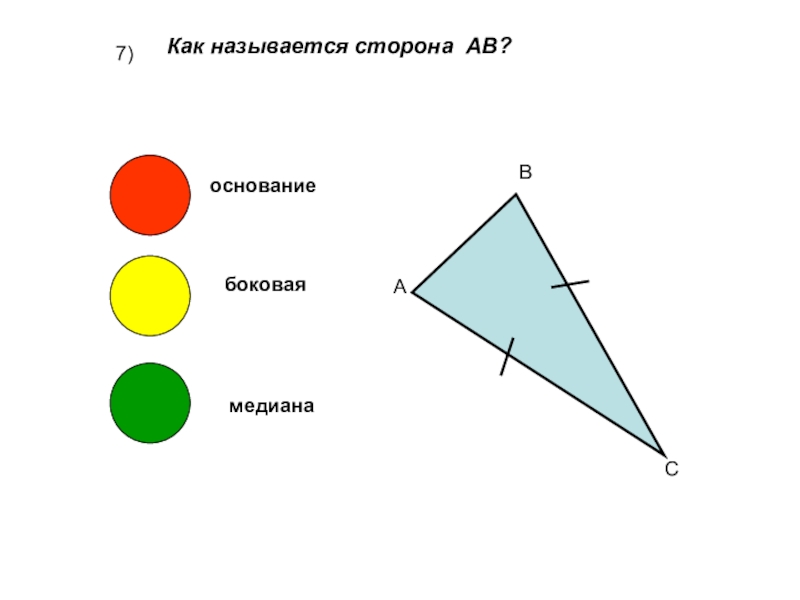
8. 7)Как называется сторона АВ? АВСоснованиебоковаямедиана
9. Построения циркулем и линейкой
10. В геометрии выделяют задачи
11. Неразрешимые задачиСледующие три задачи на построение были
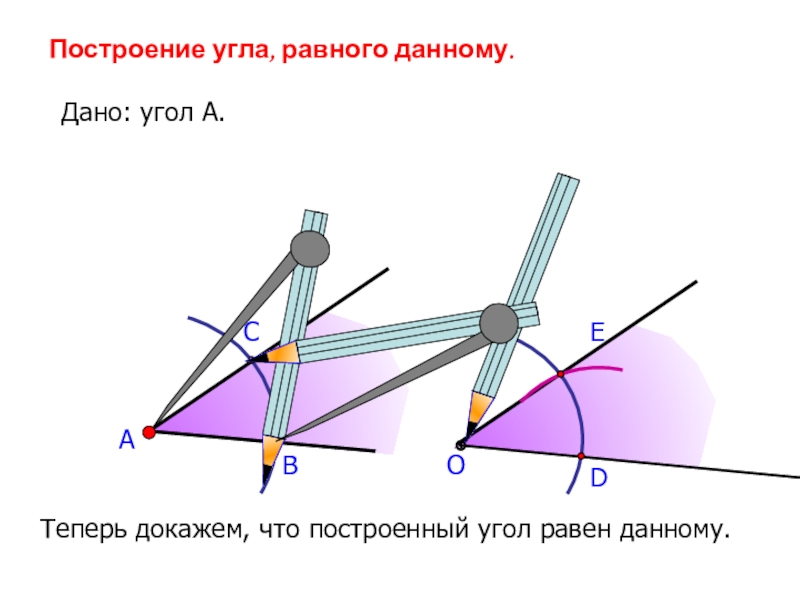
12. АВСПостроение угла, равного данному.Дано: угол А.ОDEТеперь докажем, что построенный угол равен данному.
13. Построение угла, равного данному.Дано: угол А.АПостроили угол
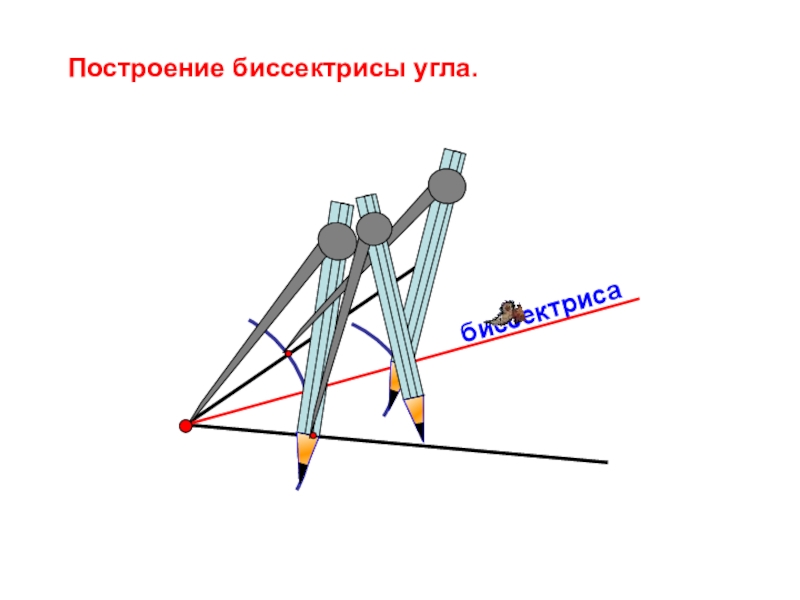
14. биссектрисаПостроение биссектрисы угла.
15. Докажем, что луч АВ – биссектриса
16. Постройте луч ОС так, чтобы луч ОА
17. Скачать презентанцию

Задания на повторение1)Укажите, на каком из приведённых ниже рисунков имеются равные треугольники?

Главная
Разное
Задачи на построение. 7 класс

Слайды и текст этой презентации

Слайд 1Задачи на построение.
7 класс

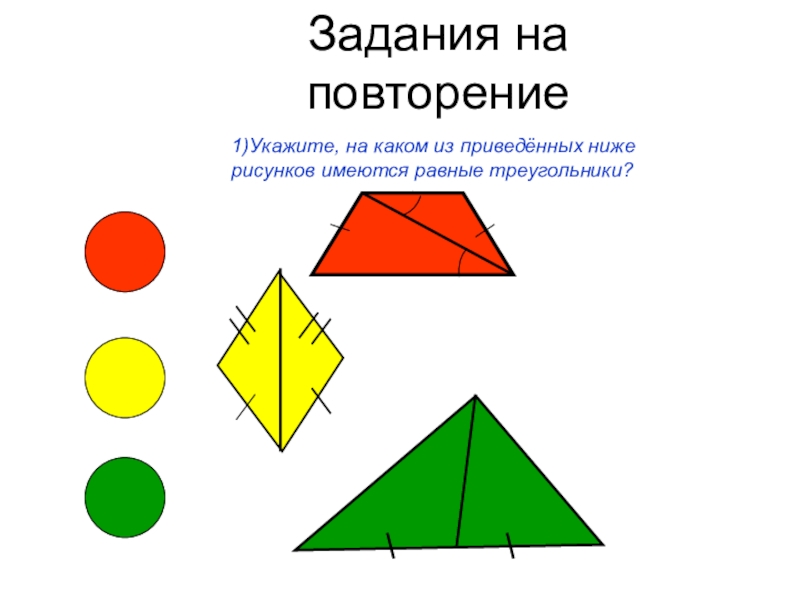
Слайд 2Задания на повторение

1)Укажите, на каком из приведённых ниже рисунков имеются

равные треугольники?

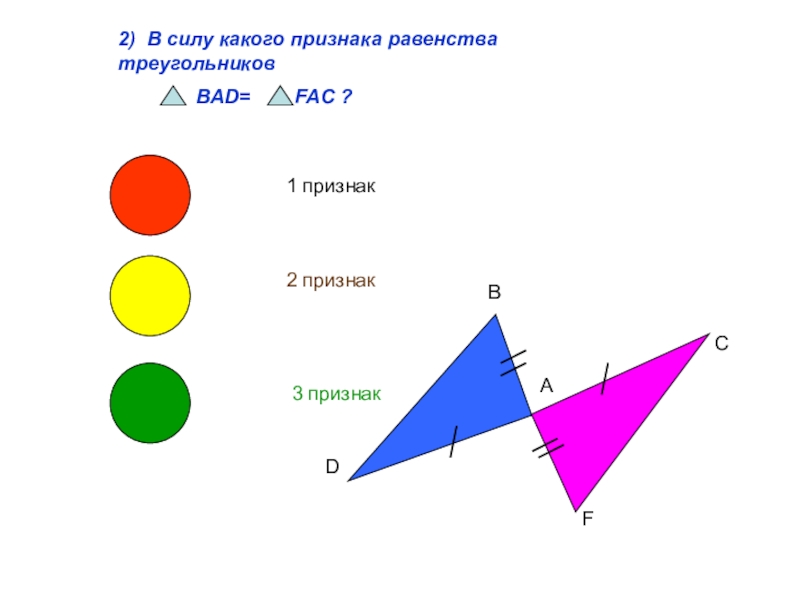
Слайд 32) В силу какого признака равенства треугольников

BAD= FAC ?
1

признак

2 признак

3 признак

2) В силу какого признака равенства треугольников BAD=

Слайд 43) В силу какого признака равенства треугольников

BAC= FAC ?
1

признак

2 признак

3 признак

3) В силу какого признака равенства треугольников BAC=

Слайд 54) < D = 80°.
Найти < F
D
B
C
A
F
60º
80º
120º

Слайд 65) CD = 5 см. Найти АВ.
А
В
О
D
C
3см
3 см
6 см
4 см
5

см

Слайд 76)
Сколько медиан можно провести в треугольнике?
Одну
Две
Три

Слайд 87)
Как называется сторона АВ?
А
В
С
основание
боковая
медиана

Слайд 9Построения
циркулем и линейкой

Слайд 10 В геометрии выделяют задачи на построение, которые

можно решить только с помощью двух инструментов: циркуля и линейки

без масштабных делений.

Линейка позволяет провести произвольную
прямую, а также построить прямую, проходящую
через две данные точки; с помощью циркуля
можно провести окружность произвольного
радиуса, а также окружность с центром в
данной точке и радиусом, равным данному
отрезку.

IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

В геометрии выделяют задачи на построение, которые можно решить только с помощью двух инструментов:

Слайд 11Неразрешимые задачи
Следующие три задачи на построение были поставлены ещё в

античности:
Трисекция угла — разбить произвольный угол на три равные части.

Удвоение куба — построить отрезок, являющийся ребром куба в два раза большего объёма, чем куб с данным ребром.
Квадратура круга — построить квадрат, равный по площади данному кругу.
Только в XIX веке было доказано, что все три задачи не разрешимы циркулем и линейкой. Вопрос возможности построения полностью решён алгебраическими методами, основанными на теории Галуа.

Неразрешимые задачиСледующие три задачи на построение были поставлены ещё в античности:Трисекция угла — разбить произвольный угол на

Слайд 12А
В
С
Построение угла, равного данному.
Дано: угол А.
О
D
E
Теперь докажем, что построенный угол

равен данному.

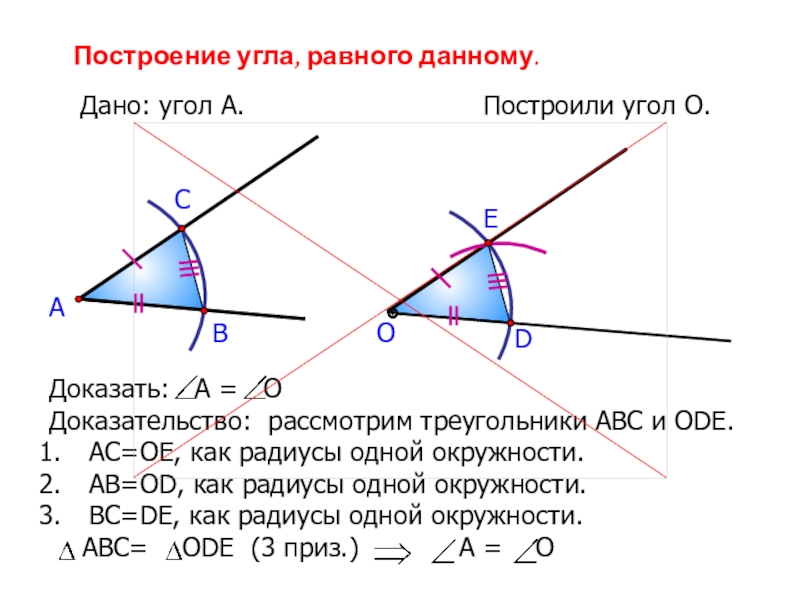
Слайд 13Построение угла, равного данному.
Дано: угол А.
А
Построили угол О.
В
С
О
D
E
Доказать: А

= О
Доказательство: рассмотрим треугольники АВС и ОDE.
АС=ОЕ, как радиусы

одной окружности.
АВ=ОD, как радиусы одной окружности.
ВС=DE, как радиусы одной окружности.
АВС= ОDЕ (3 приз.) А = О

Построение угла, равного данному.Дано: угол А.АПостроили угол О.ВСОDEДоказать: А = ОДоказательство: рассмотрим треугольники АВС и

Слайд 14биссектриса
Построение биссектрисы угла.

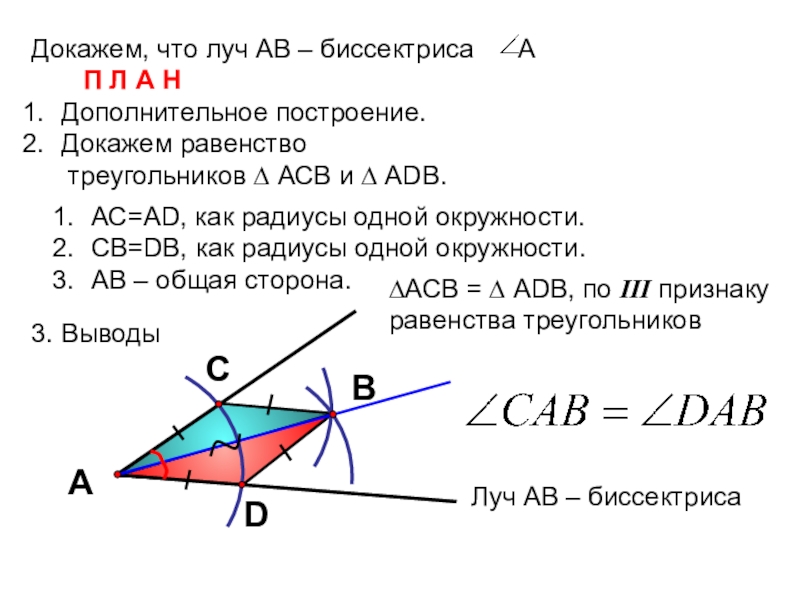
Слайд 15Докажем, что луч АВ – биссектриса А

П Л А Н
Дополнительное построение.
Докажем равенство

треугольников ∆ АСВ и ∆ АDB.

3. Выводы

АС=АD, как радиусы одной окружности.
СВ=DB, как радиусы одной окружности.
АВ – общая сторона.

∆АСВ = ∆ АDВ, по III признаку
равенства треугольников

Луч АВ – биссектриса

Слайд 16Постройте луч ОС так, чтобы луч ОА был биссектрисой угла

ВОС.
Р

е ш е н и е.
Проведём окружность произвольного радиуса с центром О. Она пересечёт лучи ОА и ОВ в точках А1 и В1.
2) Проведём окружность радиуса А1 В1 с центром А1 .Она пересечёт первую окружность в точках С и ___.
3) Проведём луч ОС. Докажем, что луч ОС искомый. Действительно, ΔОА1В1= _______
по трём_____________, поэтому ے АОВ =_______,
т.е. луч ОА - _____________________ угла ВОС