Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи с параметрами
Содержание
- 1. Задачи с параметрами
- 2. Определение Уравнение f(x;a)=0, где х- переменная, а – произвольное действительное число, называют уравнением с параметром а.
- 3. Аналитический способ решения задач с параметрамиЭтот способ
- 4. 1) Решить уравнение: ax=1 На
- 5. 2) Решить уравнение x ≠ ±2,
- 6. 0а = - 1 невозможно ни
- 7. Графический способПри решении уравнения f(x)=g(x) графическим способом
- 8. Функция у = b b
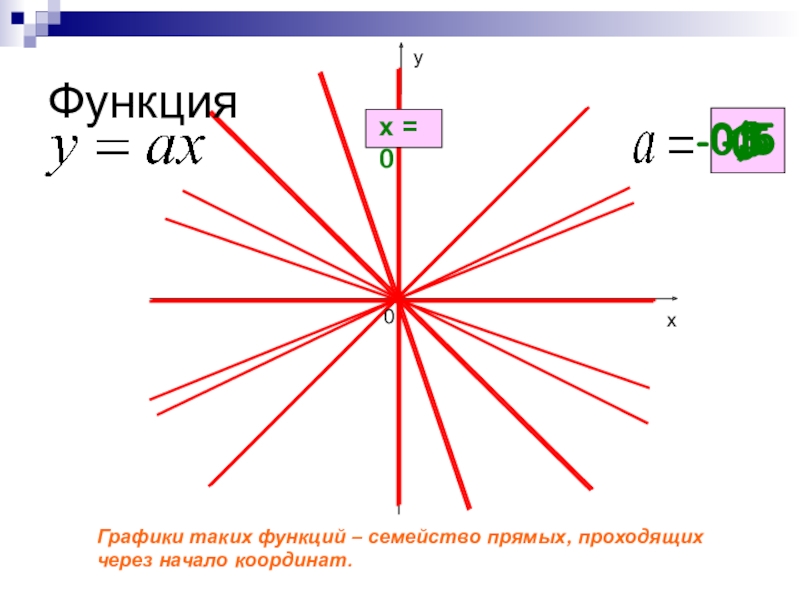
- 9. ФункцияГрафики таких функций – семейство прямых, проходящих через начало координат.00,51х = 0-3-1-0,5ху0
- 10. 2. Построим графики функции
- 11. Найдите все значения параметра р, при которых
- 12. Решение уравнений относительно параметраПри решении задач этим
- 13. Задача. Решить уравнение
- 14. Возможны различные случаи. Результаты исследования этих случаев запишем в таблицу:Ответ:если а
- 15. Задача 1. Найдите все значения а, при
- 16. Функция -
- 17. Задача 2. Найдите все положительные значения
- 18. Слайд 18
- 19. Слайд 19
- 20. Ответ: при число 1 принадлежит области определения функции.
- 21. х.Способы решения задач с параметрамиАналитическийхнеизвестная величинапараметраРешение относительно параметра
- 22. Скачать презентанцию
Определение Уравнение f(x;a)=0, где х- переменная, а – произвольное действительное число, называют уравнением с параметром а.
Слайды и текст этой презентации
Слайд 2Определение
Уравнение f(x;a)=0, где х- переменная, а – произвольное действительное
число, называют уравнением с параметром а.
Слайд 3Аналитический способ решения задач с параметрами
Этот способ повторяет стандартные процедуры
нахождения ответа в задачах без параметра.
Аналитический способ решения задач с
параметрами – самый трудный, он требует высокой грамотности и наибольших усилий по овладению им.
Слайд 4
1) Решить уравнение: ax=1
На первый взгляд представляется возможным сразу
дать ответ: х = 1/а
Однако при
a=0 данное уравнение решений не имеет.Ответ:
Если a=0, то нет решений;
Если a≠0, то х = 1/а
Слайд 52) Решить уравнение
x ≠ ±2, ax+2a = x+1,
(a-1)x=1-2a, a≠1.
Найдем значения a, которые приводят
к недопустимым значениям x.Следовательно, а не может равняться .
Слайд 7Графический способ
При решении уравнения f(x)=g(x) графическим способом строятся графики функций
y=f(x) и y=g(x) в одной системе координат.
Как известно, число корней
уравнения совпадает с количеством точек пересечения графиков построенных функций.Если график функции не зависит от параметра, то он неподвижен, а если зависит- то представляет собой семейство графиков, иначе - «подвижный» график.
y=f(x)
y=g(x)
Слайд 8Функция
у = b
b = -4
b =
-2
b = 0
b = 2
b = 4
Графики
таких функций –
семейство
параллельных
оси Ох прямых.
Слайд 9Функция
Графики таких функций – семейство прямых, проходящих
через начало координат.
0
0,5
1
х
= 0
-3
-1
-0,5
х
у
0
Слайд 102. Построим графики функции
и рассмотрим
различные случаи в
зависимости от параметра .
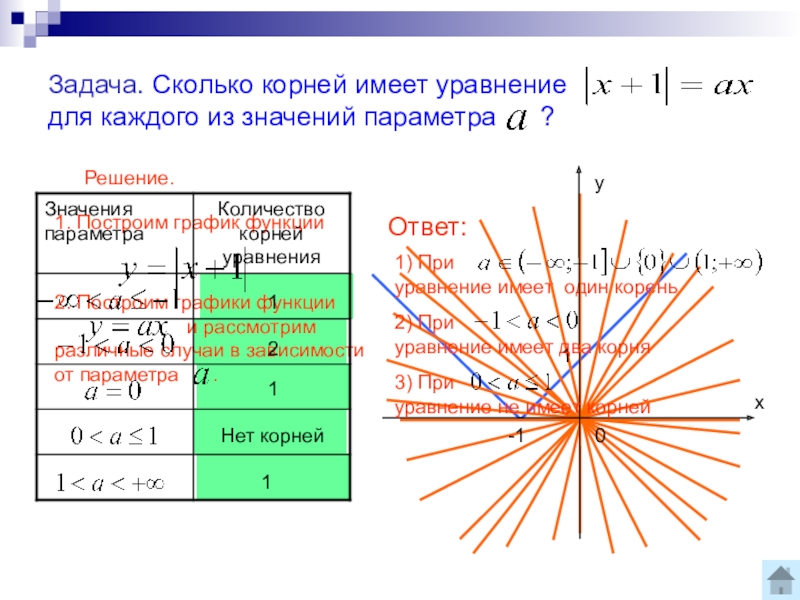
Задача. Сколько корней имеет уравнение
для каждого из значений параметра ?
Решение.
1. Построим график функции
Ответ:
1) При
уравнение имеет один корень
1
2
1
Нет корней
1
2) При
уравнение имеет два корня
3) При
уравнение не имеет корней
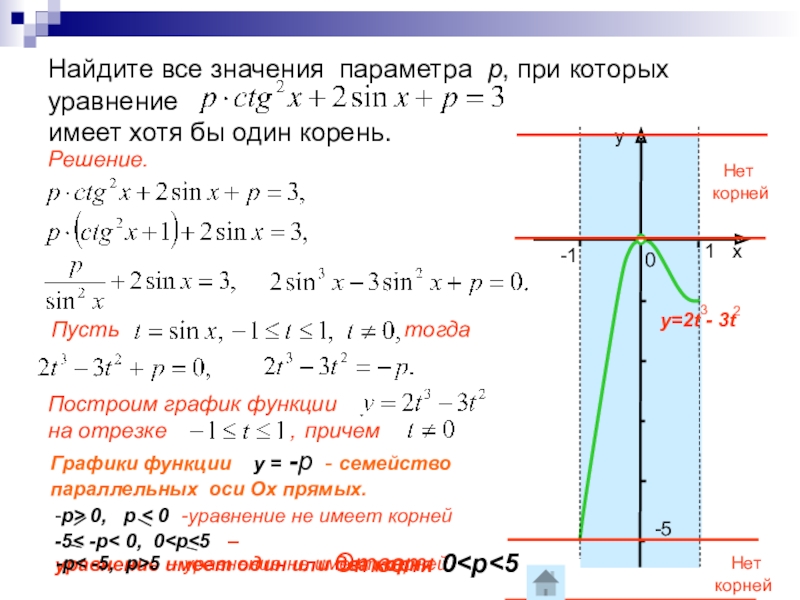
Слайд 11Найдите все значения параметра р, при которых уравнение имеет хотя бы
один корень.
-5
Решение.
Пусть
Построим график функции
на отрезке
, тогда
причем
Графики функции у = -р - семейство
параллельных оси Ох прямых.
Нет
корней
Нет
корней
-р< -5, p>5 – уравнение не имеет корней
Ответ: 0
Слайд 12Решение уравнений относительно параметра
При решении задач этим способом переменные х
и а принимаются равноправными и выбирается та переменная, относительно которой
аналитическое решение признается более простым. После естественных упрощений возвращаемся к исходному смыслу переменных х и а и заканчиваем решение.
Слайд 13Задача. Решить уравнение
Решение.
Данное уравнение
четвертой степени относительно переменной х и является квадратным относительно параметра
.а
Слайд 14Возможны различные случаи. Результаты
исследования этих случаев запишем в таблицу:
Ответ:
если
а
;если -1 если а=1, то ; если а>1, то .
Слайд 15Задача 1. Найдите все значения а, при которых область определения
функции
содержит ровно три целых числа.
Преобразуем
выражение в скобках:Решение.
Областью определения данной функции
является множество решений системы неравенств:
Слайд 16Функция - монотонно убывает или
возрастает в зависимости от
значения параметра а.
при . а
+
_
+
+
_
_
Рассмотрим различные случаи в зависимости от значений параметра а.
1. 0 Это множество включает в себя 2. 1 Решим первое неравенство: Пусть , . Это множество может 3. а>4, a _ Данное множество содержит Ответ: х х
бесконечное число целых чисел.
Функция - убывающая при любом значении параметра а.
при .
содержать только два целых числа.
три целых числа, если
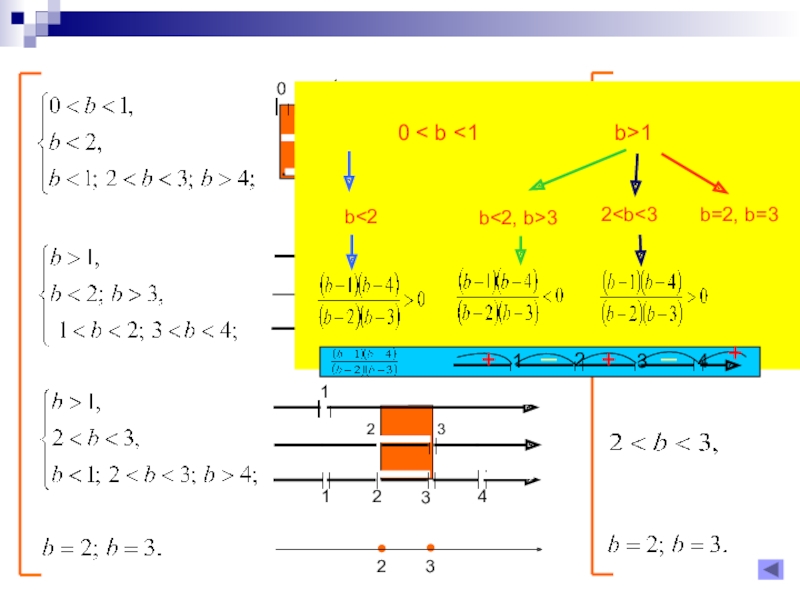
Слайд 17Задача 2. Найдите все положительные значения параметра b, при
которых число 1 принадлежит области определения функции
Решение.
Найдем область определения данной
функции.Для положительных значений b рассмотрим три различных случая
Слайд 21х
.
Способы решения задач с параметрами
Аналитический
х
неизвестная величина
параметр
а
Решение относительно параметра
