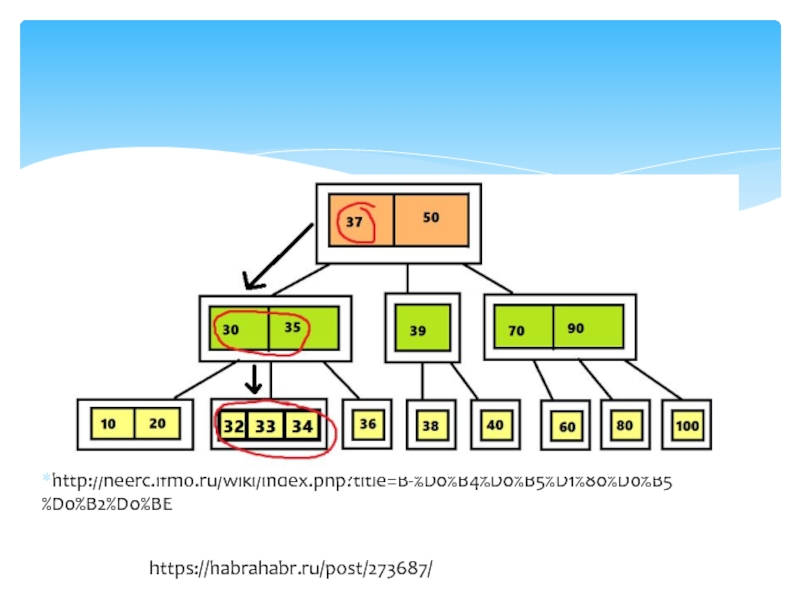
Слайд 2http://neerc.ifmo.ru/wiki/index.php?title=B-%D0%B4%D0%B5%D1%80%D0%B5%D0%B2%D0%BE
https://habrahabr.ru/post/273687/
Слайд 3дерево как конечное множество T, состоящее из одного или более
элементов (называемых вершинами или узлами), таких, что
имеется одна специально выделенная
вершина, называемая корнем дерева;
остальные вершины (исключая корень) содержатся в m попарно непересекающихся множествах T1,T2,...,Tm, каждое из которых, в свою очередь, является деревом.
Деревья T1,T2,...Tm называются поддеревьями данного дерева.
Упорядоченным деревом мы будем называть такое дерево, в котором важен порядок следования поддеревьев T1,T2,...Tm.
Определение 1
Слайд 4Дуга - это ориентированная связь между двумя вершинами дерева, поэтому,
например, корень можно определить как такую вершину дерева, в который
не входит ни одной дуги, поэтому часто говорят, что корень - это "исходная" вершина дерева, через которую доступны остальные его вершины.
Ребро - это неориентированная связь между двумя вершинами дерева. Ясно, что ребро можно превратить в дугу, если задать на нем ориентацию (направление), а любое дерево можно превратить в ориентированное дерево, если задать ориентацию ребер.
Количество поддеревьев некоторой вершины называется степенью этой вершины. Деревья, имеющие степень больше 2, называются сильно ветвящимися деревьями.
Вершина с нулевой степенью называется листом, иначе - она называется внутренней вершиной (внутренним узлом).
Число листьев дерева называется весом дерева.
Символы A,B,C,..., которые служат для обозначения вершин, называются метками вершин.
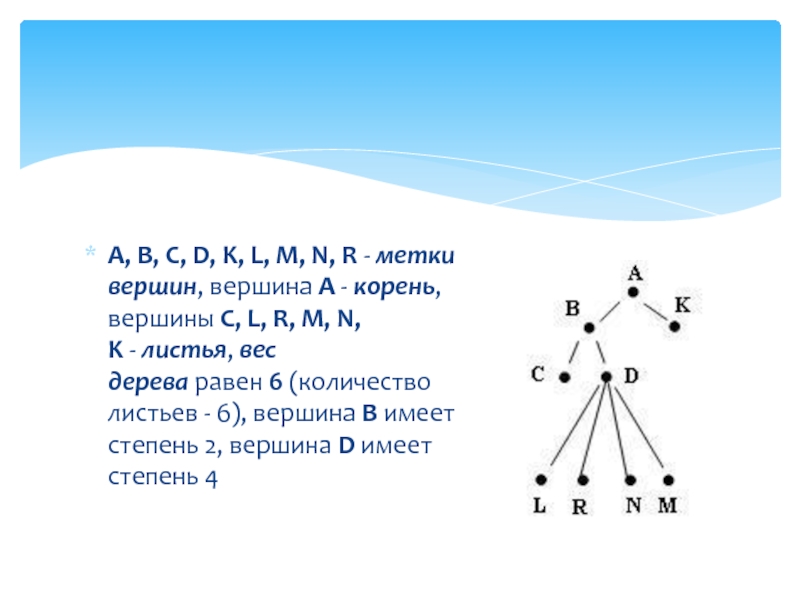
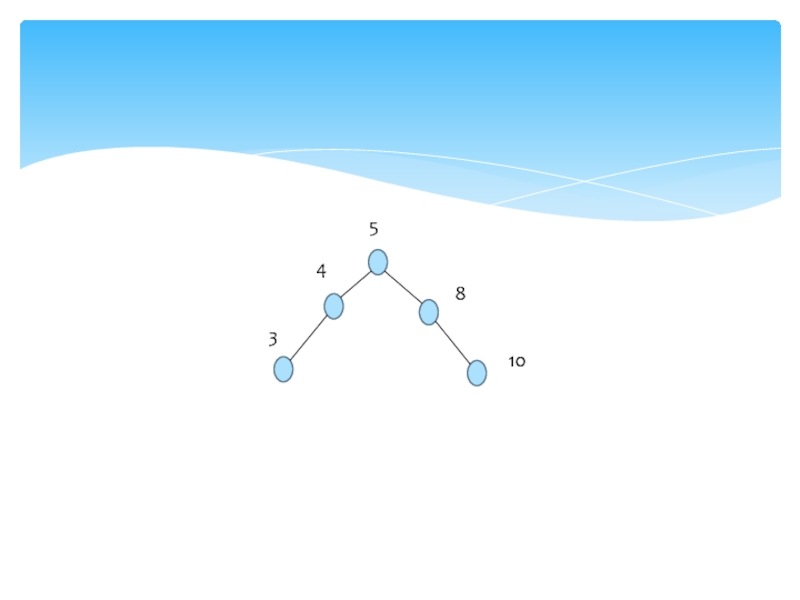
Слайд 5A, B, C, D, K, L, M, N, R - метки вершин,
вершина А - корень, вершины C, L, R, M, N, K - листья, вес дерева равен 6 (количество листьев -
6), вершина В имеет степень 2, вершина D имеет степень 4
Слайд 6Вершина Y, которая находится непосредственно под узлом X, называется (непосредственным)
потомком (сыном) X, вершина X в данном случае называется (непосредственным)
предком (отцом) Y.
В этом случае, если вершина X находится на уровне i, то говорят, что вершина Y находится на уровне i+1. Мы будем считать, что корень дерева расположен на уровне 0. Максимальный уровень какой-либо вершины дерева называется его глубиной или высотой.
Максимальная степень всех вершин дерева называется степенью дерева.
Определение 2
Слайд 7если вершина не имеет потомков, то она является листом;
степень внутренней вершины
можно определить как число ее (непосредственных) потомков.
Следствия
Слайд 8максимальное число вершин для дерева с высотой h и степенью d можно найти по
формуле
Слайд 9Количество дуг, которые нужно пройти, чтобы продвинуться от корня к
вершине X, называется длиной пути к вершине X.
Вершина, расположенная
на уровне i, имеет длину пути i.
Ветвью будем называть путь от корня дерева к любому ее листу.
Длина пути дерева определяется как сумма длин путей ко всем его вершинам. Она также называется длиной внутреннего пути дерева.
Определение 3
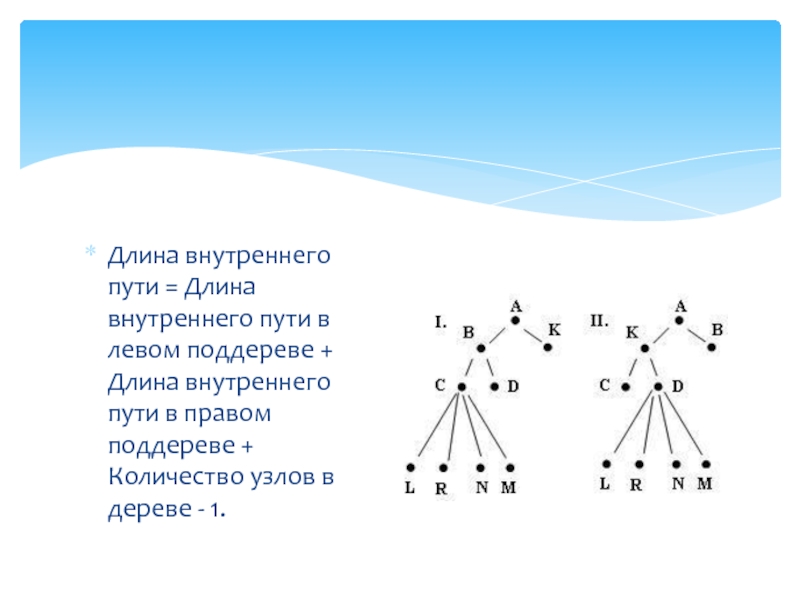
Слайд 10Длина внутреннего пути = Длина внутреннего пути в левом поддереве
+ Длина внутреннего пути в правом поддереве + Количество узлов
в дереве - 1.
Слайд 11Лес - это множество деревьев (обычно упорядоченное), состоящее из некоторого
(быть может, равного нулю) числа непересекающихся деревьев. Часто для леса,
состоящего из n деревьев пользуются термином "дерево с n-кратным корнем".
Определение 4
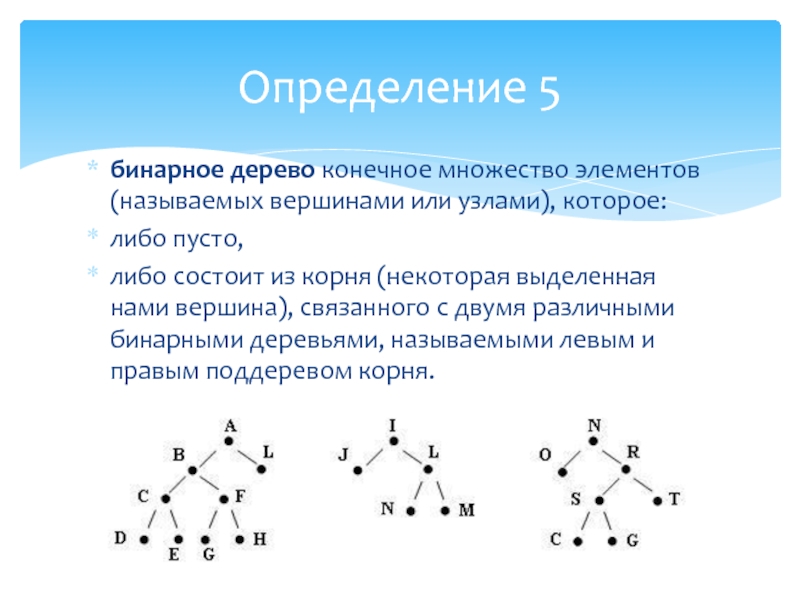
Слайд 12бинарное дерево конечное множество элементов (называемых вершинами или узлами), которое:
либо
пусто,
либо состоит из корня (некоторая выделенная нами вершина), связанного с
двумя различными бинарными деревьями, называемыми левым и правым поддеревом корня.
Определение 5
Слайд 14два бинарных дерева T и T' подобны, если они имеют
одинаковую структуру; это означает, что подобные деревья либо оба пусты,
либо оба непусты и их левые и правые поддеревья соответственно подобны.
Попросту говоря, подобие означает, что графические изображения деревьев T и T' имеют одинаковую "конфигурацию".
Определение 6
Слайд 15бинарные деревья T и T' эквивалентны, если они подобны и
если, кроме того, соответствующие вершины содержат одинаковую информацию.
Если
Info (u) обозначает информацию, содержащуюся в вершине u, то формально деревья эквивалентны тогда и только тогда, когда они:
либо оба пусты,
либо же оба непусты, Info (Корень(T))=Info (Корень(T')) и их левые и правые поддеревья соответственно эквивалентны.
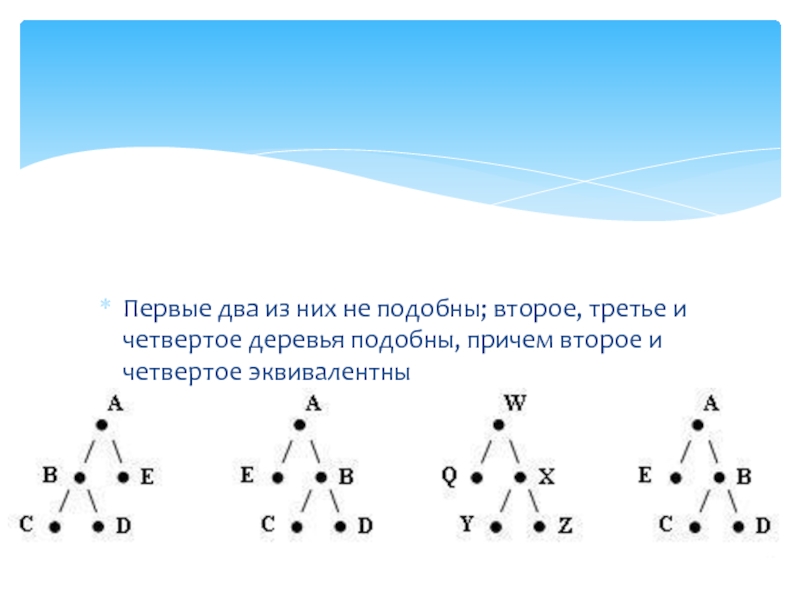
Слайд 16Первые два из них не подобны; второе, третье и четвертое
деревья подобны, причем второе и четвертое эквивалентны
Слайд 17Каждая вершина бинарного дерева является структурой, состоящей из четырех полей:
информационное
поле (ключ вершины),
служебное поле (их может быть несколько!),
указатель на левое
поддерево,
указатель на правое поддерево.
Бинарные деревья поиска
Слайд 18struct node
{
int Key; //
Ключ вершины.
int Count; // Счетчик количества
вершин с одинаковыми ключами.
node *Left; // Указатель на "левого" сына.
node *Right; // Указатель на "правого" сына.
};
Слайд 19Tree - указатель на корень дерева
p - вспомогательный указатель на вершину дерева
Построение
бинарного дерева поиска
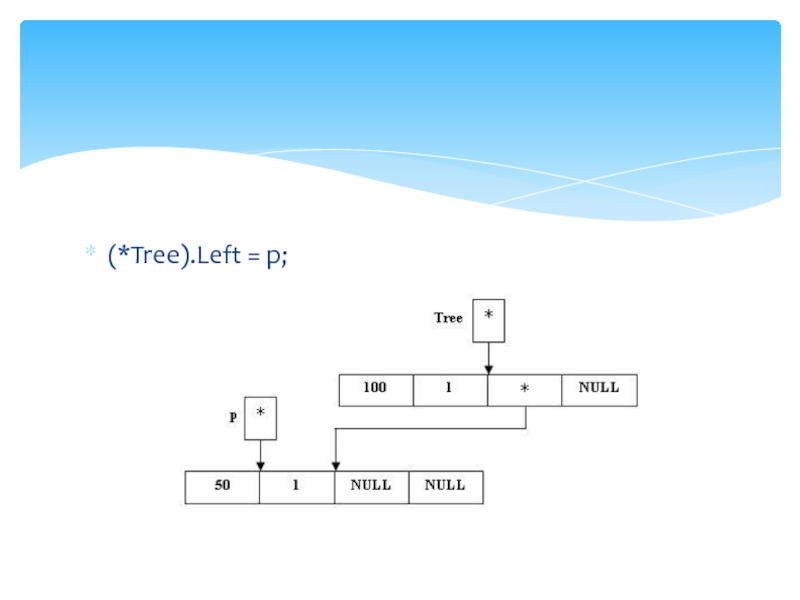
Слайд 20 Tree = NULL; //Построение пустого дерева
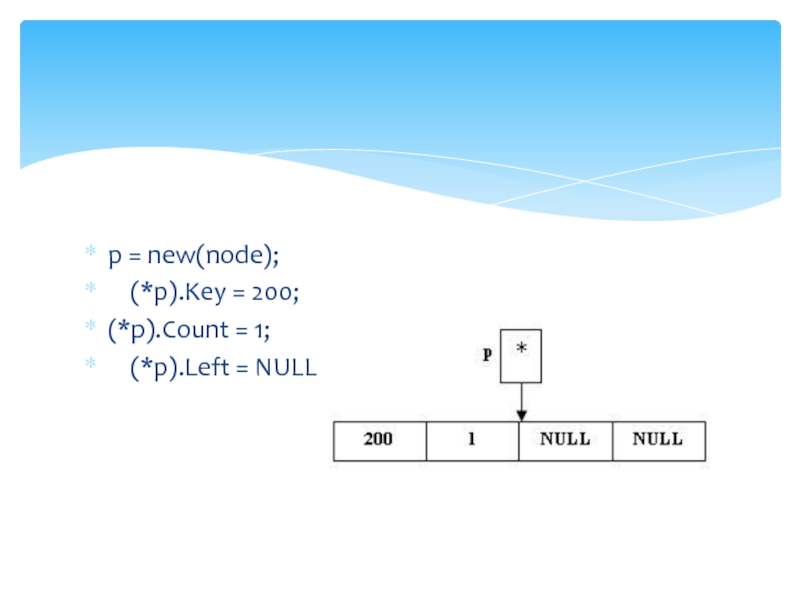
p = new(node);
(*p).Key = 100;
(*p).Count = 1;
(*p).Left = NULL;
(*p).Right = NULL;
Tree = p;
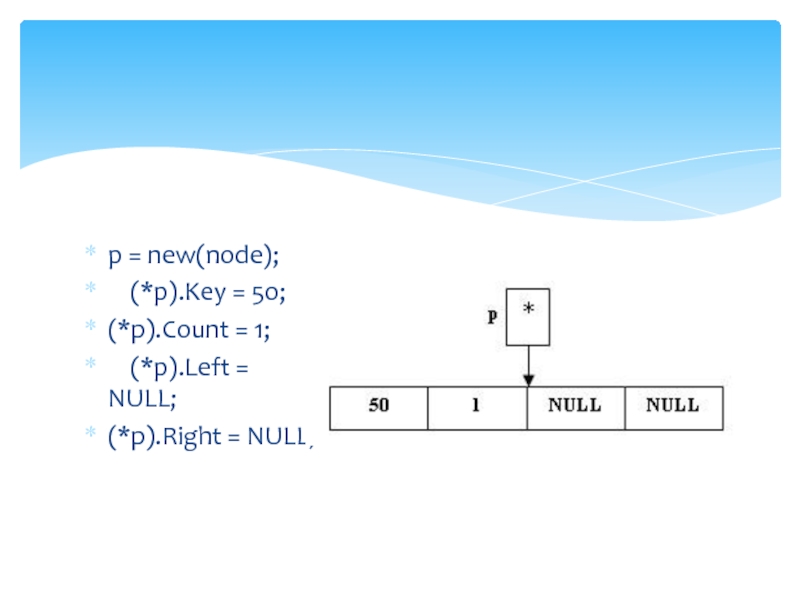
Слайд 21p = new(node);
(*p).Key = 50;
(*p).Count = 1;
(*p).Left = NULL;
(*p).Right = NULL;
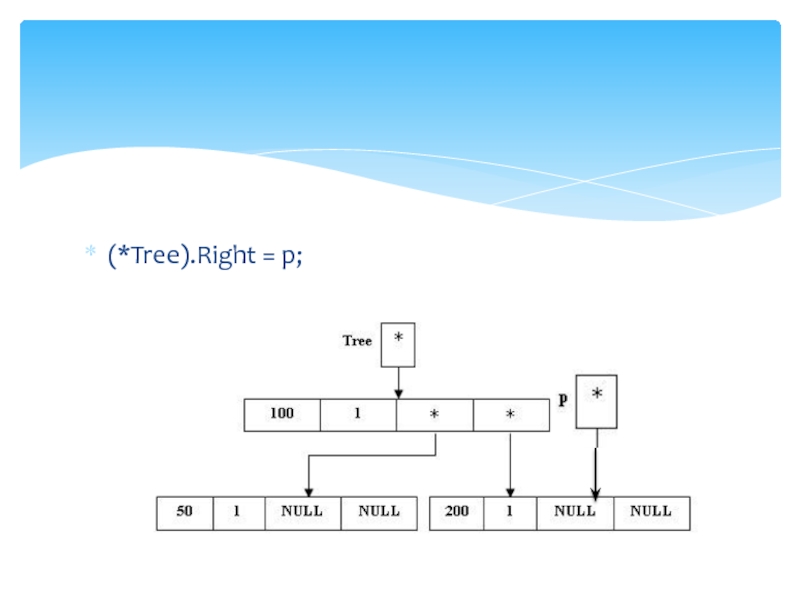
Слайд 23p = new(node);
(*p).Key = 200;
(*p).Count = 1;
(*p).Left = NULL; (*p).Right = NULL;
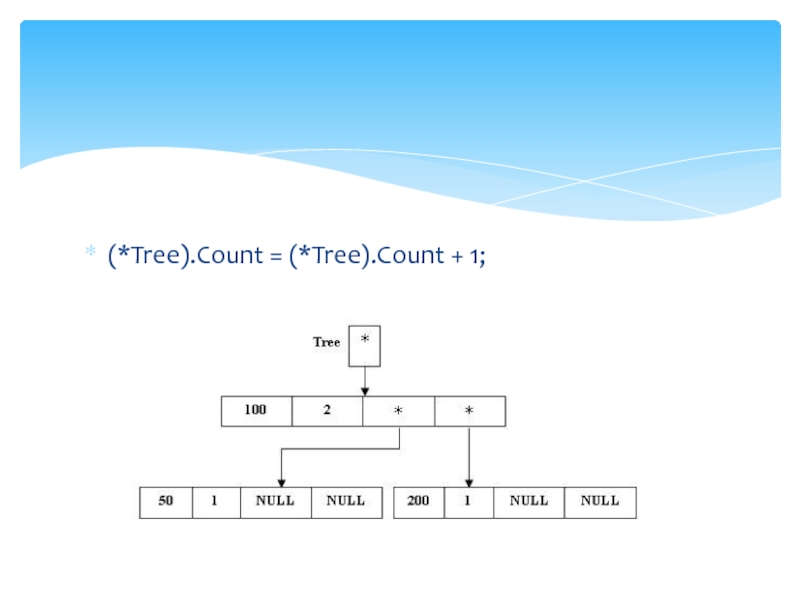
Слайд 25(*Tree).Count = (*Tree).Count + 1;
Слайд 26void BuildTree (node **Tree)
// Построение бинарного дерева.
// *Tree -
указатель на корень дерева.
{
int el;
*Tree = NULL; //
Построено пустое бинарное дерево.
cout<<"Вводите ключи вершин дерева...\n";
cin>>el;
while (el!=0)
{ Search (el,Tree); cin>>el;}
}
Слайд 27void Search (int x, node **p)
// Поиск вершины с ключом
x в дереве со вставкой
// (рекурсивный алгоритм).
// *p -
указатель на корень дерева.
{
if (*p==NULL)
{
// Вершины с ключом x в дереве нет; включить ее.
*p = new(node);
(**p).Key = x;
(**p).Count = 1;
(**p).Left = (**p).Right = NULL;
}
else
//Поиск места включения вершины.
if (x<(**p).Key)
//Включение в левое поддерево.
Search (x,&((**p).Left));
else if (x>(**p).Key)
//Включение в правое поддерево.
Search (x,&((**p).Right));
else (**p).Count = (**p).Count + 1;
}
Слайд 28Теоpема Хопкpофта-Ульмана
Сpеднее число сpавнений, необходимых для вставки n случайных элементов
в деpево поиска, пустое вначале, pавно O(nlog2n) для n>=1.
Анализ алгоpитма
поиска с включениями
Слайд 29A B D M N E C
B D C
E R
посетите корень дерева;
обойдите левое поддерево;
обойдите правое поддерево.
Левосторонний обход
бинарного дерева поиска
Слайд 30void ObhodLeft (node **w)
// Левосторонний обход дерева.
// *w - указатель
на корень дерева.
{
if (*w!=NULL)
{ cout
ObhodLeft (&((**w).Left));
ObhodLeft (&((**w).Right)); }
}
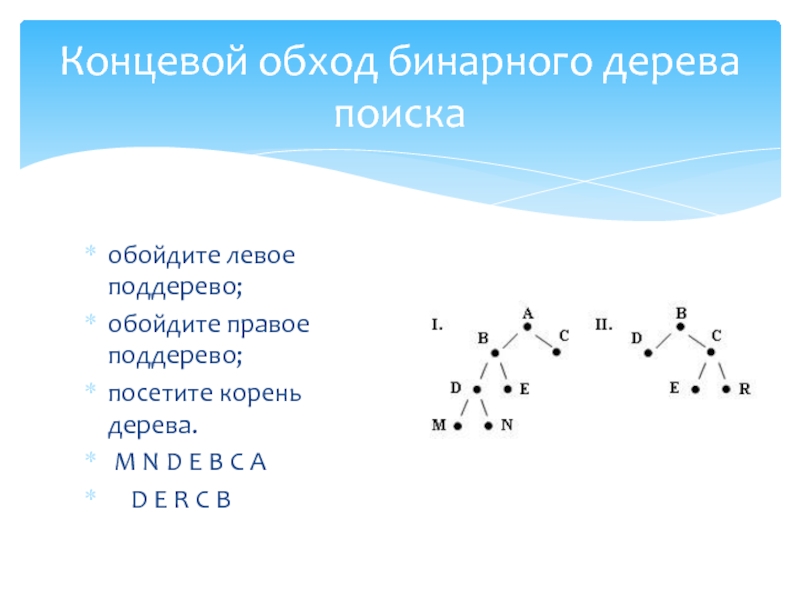
Слайд 31обойдите левое поддерево;
обойдите правое поддерево;
посетите корень дерева.
M N D
E B C A
D E R C B
Концевой обход бинарного дерева поиска
Слайд 32void ObhodEnd (node **w)
// Концевой обход дерева.
// *w - указатель
на корень дерева.
{
if (*w!=NULL)
{ ObhodEnd (&((**w).Left));
ObhodEnd (&((**w).Right));
cout<<(**w).Key<<" ";}
}
Слайд 33обойдите левое поддерево;
посетите корень дерева;
обойдите правое поддерево.
M D N B
E A C
D B E C R
Обратный
обход бинарного дерева поиска
Слайд 34void ObhodBack (node **w)
// Обратный обход бинарного дерева.
// *w -
указатель на корень дерева.
{
if (*w!=NULL)
{ ObhodBack (&((**w).Left));
cout<<(**w).Key<<" ";
ObhodBack (&((**w).Right)); }
}
Слайд 35void Vyvod (node **w,int l)
// Изображение дерева w на экране
дисплея.
// (рекурсивный алгоритм).
// *w - указатель на корень дерева.
{
int
i;
if (*w!=NULL)
{ Vyvod (&((**w).Right),l+1);
for (i=1; i<=l; i++) cout<<" ";
cout<<(**w).Key<
Vyvod (&((**w).Left),l+1); }
}
Вывод бинарного дерева поиска
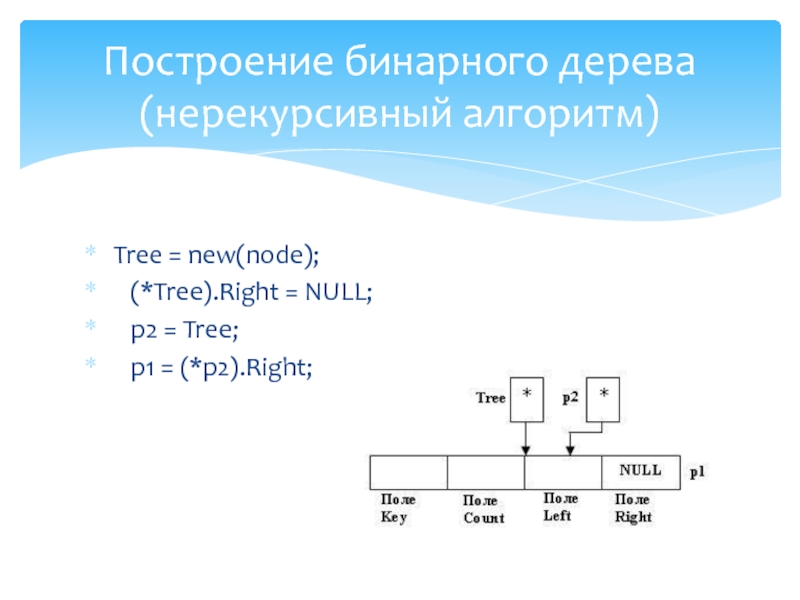
Слайд 36 Tree = new(node);
(*Tree).Right = NULL;
p2
= Tree;
p1 = (*p2).Right;
Построение бинарного дерева (нерекурсивный алгоритм)
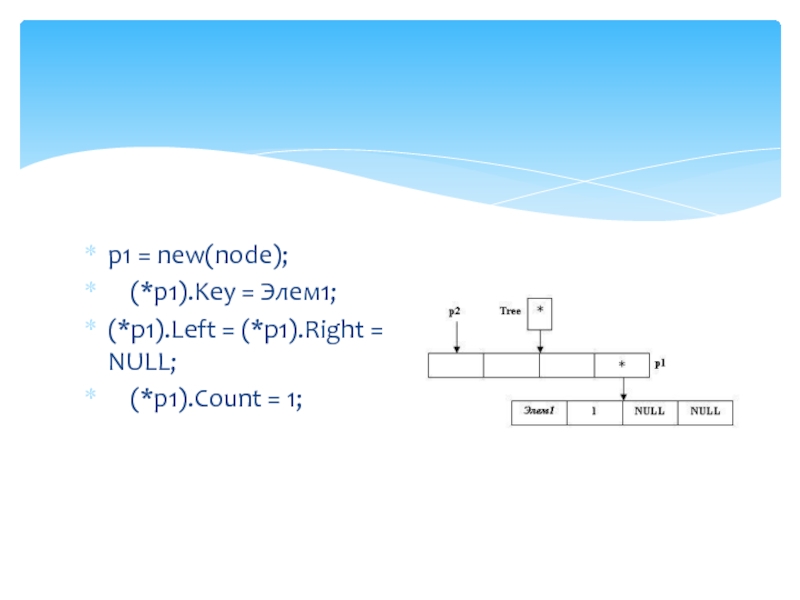
Слайд 37p1 = new(node);
(*p1).Key = Элем1;
(*p1).Left = (*p1).Right
= NULL;
(*p1).Count = 1;
Слайд 38void TreeSearch (node **Tree,int el)
// Поиск вершины с информационным полем
el в дереве
// с последующим включением.
// *Tree - указатель на
корень дерева.
{
node *p1;
node *p2; // Указатель p2 "опережает" указатель p1.
int d; // Флаг для распознавания поддеревьев.
p2 = *Tree; p1 = (*p2).Right;
d = 1; // Флаг правого поддерева.
while (p1!=NULL && d!=0)
{ p2 = p1;
if (el<(*p1).Key) { p1 = (*p1).Left; d = -1; //Флаг левого поддерева. }
else
if (el>(*p1).Key) { p1 = (*p1).Right; d = 1; }
else d = 0; }
if (d==0) (*p1).Count = (*p1).Count + 1;
else
{ p1 = new(node);
(*p1).Key = el; (*p1).Left = (*p1).Right = NULL; (*p1).Count = 1;
if (d<0) (*p2).Left = p1; else (*p2).Right = p1;}
}
Слайд 39 struct no
{
no *sled;
// Указатель на вершину.
node *elem; // Информационное
поле.
int ch; // Уровень вершины.
}
Изображение бинарного дерева (нерекурсивный алгоритм)
Слайд 40Создание БД
Поиск по БД
Левосторонний обход БД
Обратный обход БД
Концевой обход БД