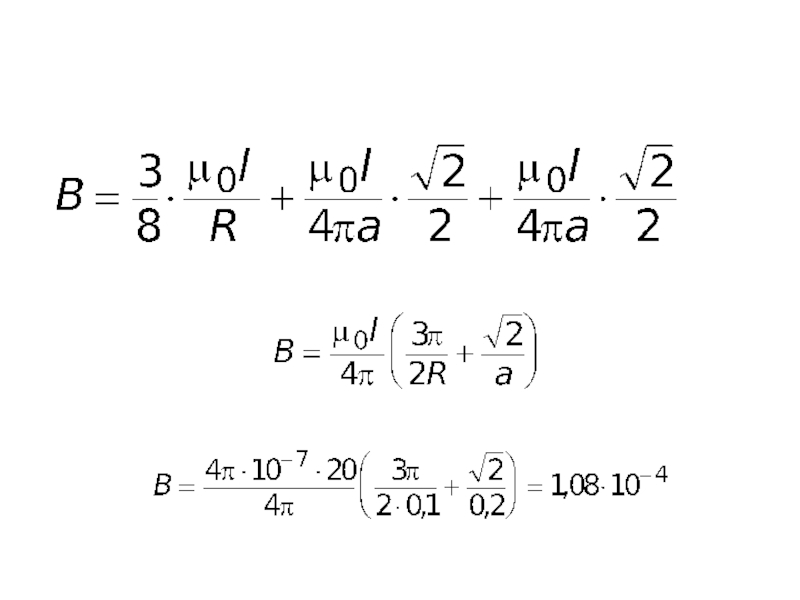Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Закон Био-Савара-Лапласа
Содержание
- 1. Закон Био-Савара-Лапласа
- 2. Индукция магнитного поля в вакууме, создаваемого бесконечно
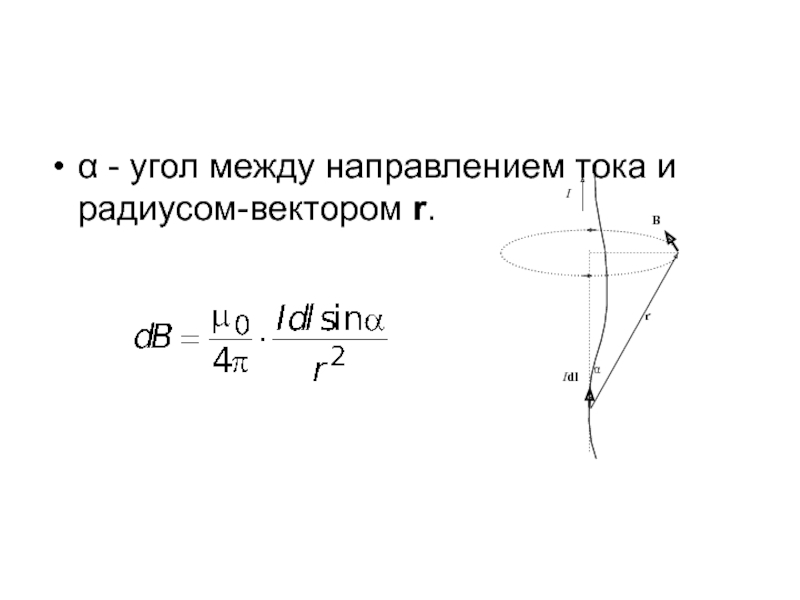
- 3. - угол между направлением тока и радиусом-вектором r.
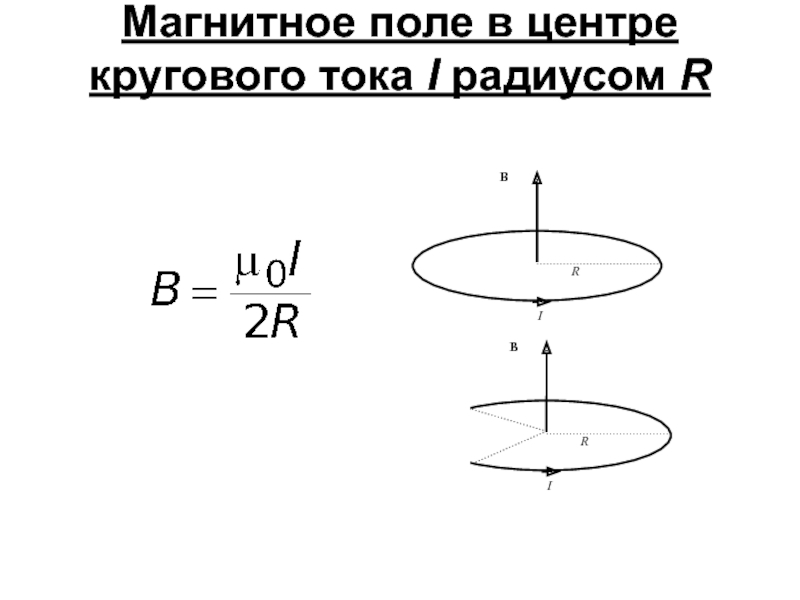
- 4. Магнитное поле в центре кругового тока I радиусом R
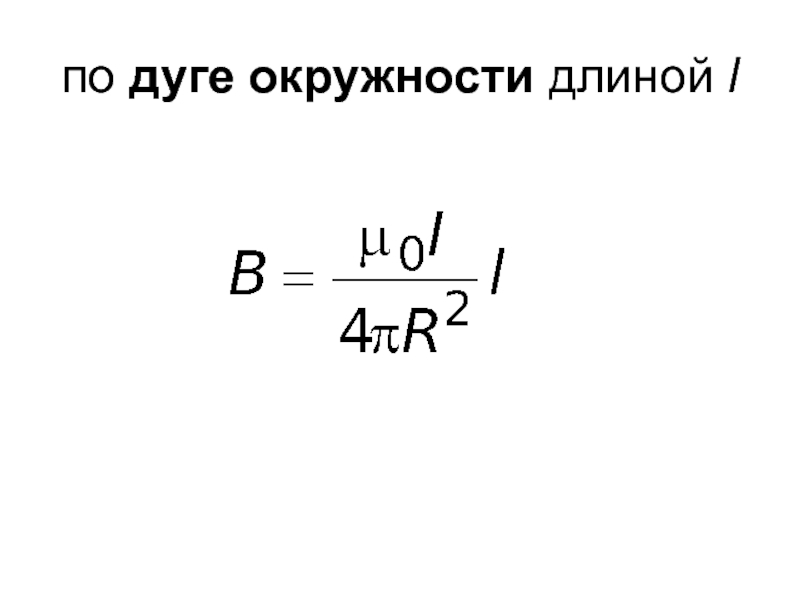
- 5. по дуге окружности длиной l
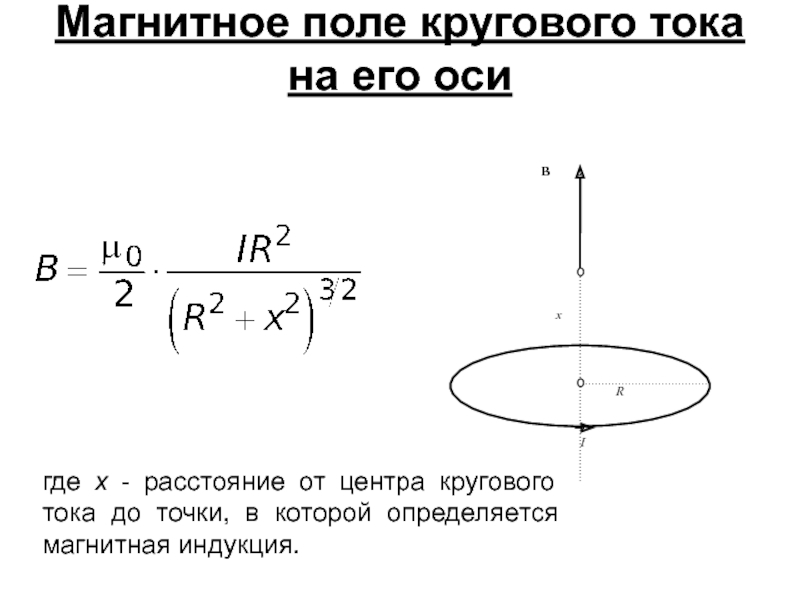
- 6. Магнитное поле кругового тока на его оси
- 7. Индукция магнитного поля прямолинейного отрезка проводника с
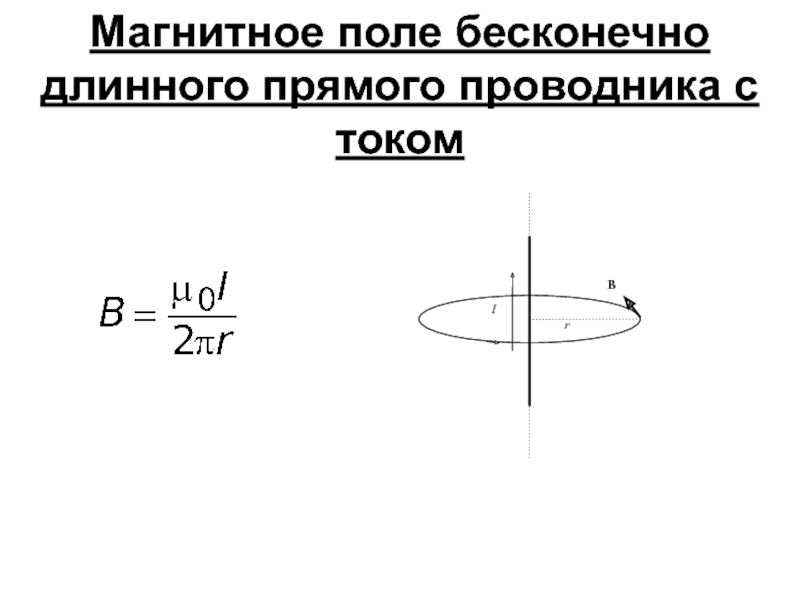
- 8. Магнитное поле бесконечно длинного прямого проводника с током
- 9. правилом правого винта (правилом буравчика) поступательное движение
- 10. Принцип суперпозиции полей Если поле создано системой
- 11. Задача 1На рисунке изображены сечения трех проводников,
- 12. Решение 1Переномеруем проводники с токами и обозначим
- 13. где .
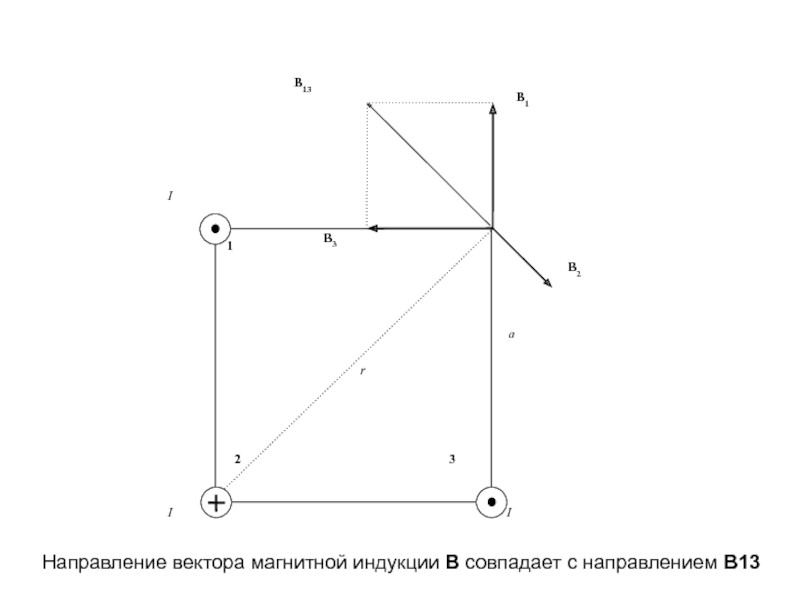
- 14. Направление вектора магнитной индукции В совпадает с направлением В13
- 15. Сначала сложим векторы В1 и В3. Из
- 16. В13 и В2 направлены в противоположные стороны,
- 17. Задача 2Найти индукцию магнитного поля, создаваемого контуром
- 18. РешениеУчасток 1 имеет форму дуги окружности длиной Этот вектор направлен перпендикулярно плоскости рисунка “от нас”.
- 19. Участки 2 и 5 представляют собой отрезки
- 20. Участок 3 - это отрезок прямого проводника,
- 21. Аналогично можно получить выражение для индукции магнитного поля, создаваемого участком 4.
- 22. Векторы В3 и В4 также перпендикулярны плоскости
- 23. Слайд 23
- 24. Скачать презентанцию
Индукция магнитного поля в вакууме, создаваемого бесконечно малым элементом проводника, по которому течет ток I. где 0 - магнитная постоянная, - элемент линейного тока, r - радиус-вектор, проведенный от элемента тока
Слайды и текст этой презентации
Слайд 2Индукция магнитного поля в вакууме, создаваемого бесконечно малым элементом проводника,
по которому течет ток I.
- элемент линейного тока, r - радиус-вектор, проведенный от элемента тока к точке, в которой рассчитывается поле, 
Слайд 6Магнитное поле кругового тока на его оси
где х - расстояние
от центра кругового тока до точки, в которой определяется магнитная
индукция.
Слайд 7Индукция магнитного поля прямолинейного отрезка проводника с током
где r -
кратчайшее расстояние от проводника до точки, в которой определяется магнитная
индукция, 1 и 2 - углы между элементами тока на концах проводника и радиус-векторами, проведенными от элементов к точке наблюдения.
Слайд 9правилом правого винта (правилом буравчика)
поступательное движение винта совпадает с
направлением тока в проводнике, вращательное движение - с направлением линии
вектора В.
Слайд 10Принцип суперпозиции полей
Если поле создано системой проводников с токами
I1, I2, I3, ..., каждый из которых создает поле с
индукцией В1, В2, В3, ..., то индукция результирующего поля равна векторной сумме индукций полей, создаваемых отдельными проводниками:.
Слайд 11Задача 1
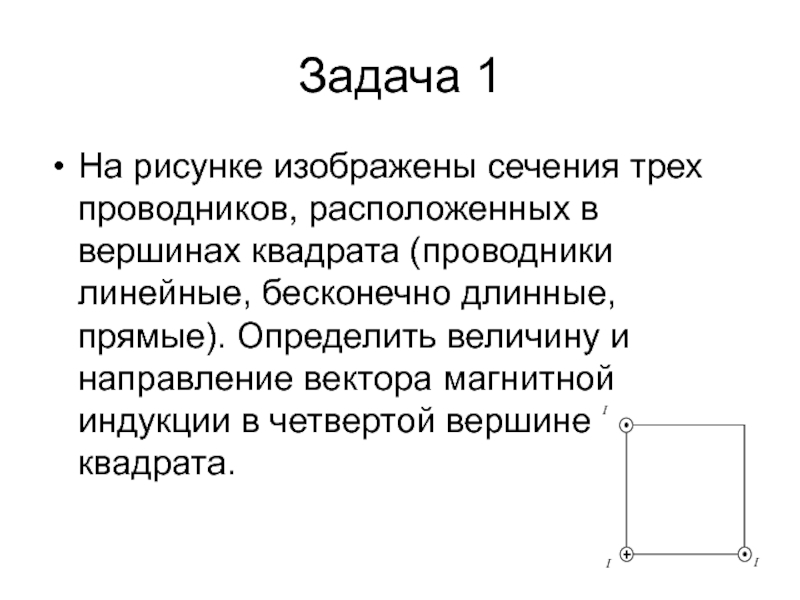
На рисунке изображены сечения трех проводников, расположенных в вершинах
квадрата (проводники линейные, бесконечно длинные, прямые). Определить величину и направление
вектора магнитной индукции в четвертой вершине квадрата.
Слайд 12Решение 1
Переномеруем проводники с токами и обозначим длину стороны квадрата
через а.
Индукция магнитного поля, создаваемого прямыми длинными проводниками с
одинаковыми токами рассчитывается по формуле ,
Слайд 13где . Следовательно, длина
вектора В2 меньше длин векторов В1 и В3.
Построим векторы магнитной
индукции в вершине квадрата и применим принцип суперпозиции полей . 
Слайд 16В13 и В2 направлены в противоположные стороны, поэтому величина индукции
магнитного поля в рассматриваемой точке равна
Слайд 17Задача 2
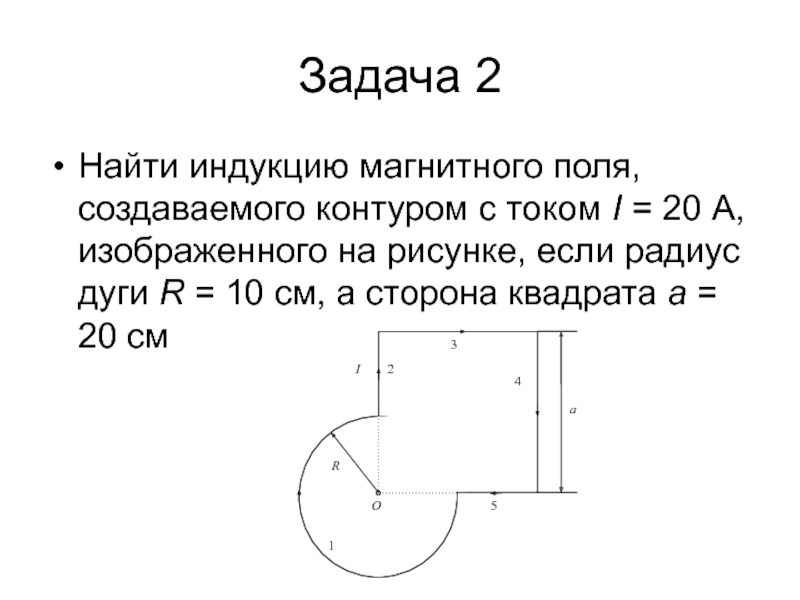
Найти индукцию магнитного поля, создаваемого контуром с током I = 20 А,
изображенного на рисунке, если радиус дуги R = 10 см,
а сторона квадрата а = 20 см
Слайд 18Решение
Участок 1 имеет форму дуги окружности длиной
Этот вектор направлен
перпендикулярно плоскости рисунка “от нас”.
Слайд 19Участки 2 и 5 представляют собой отрезки прямых, продолжения которых
проходят через точку О.
- угол между направлением тока и
направлением на точку О. Для любого элемента участка 2 = , , dB = 0; для любого элемента участка 5 = 0,
, dB = 0. Следовательно, B2 =. B5 = 0.
Слайд 20Участок 3 - это отрезок прямого проводника, к которому можно
применить формулу
где r = a,
,
,
,
Слайд 22Векторы В3 и В4 также перпендикулярны плоскости рисунка и направлены
“от нас”.
Согласно принципу суперпозиции полей
. Подставляя полученные выражения для
полей всех участков, найдем индукцию магнитного поля в точке О
