Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
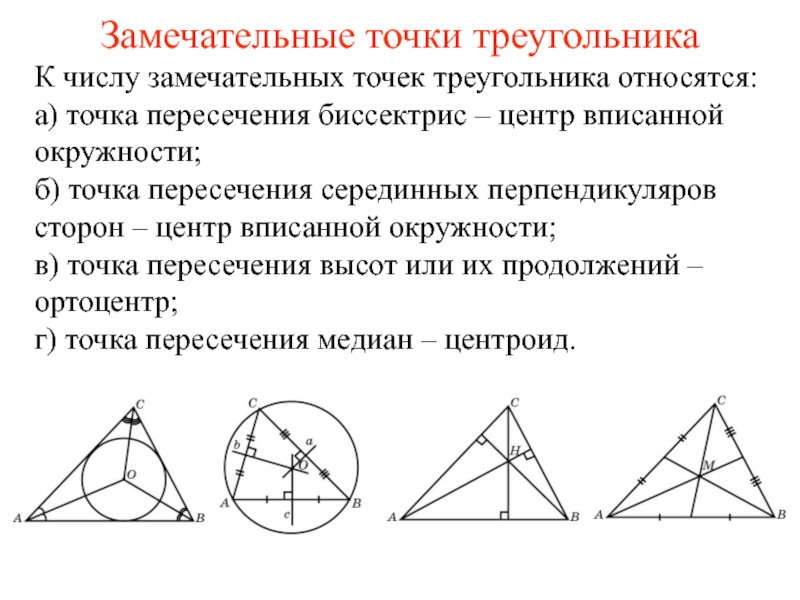
Замечательные точки треугольника
Содержание
- 1. Замечательные точки треугольника
- 2. Теорема 1Высоты треугольника или их продолжения пересекаются
- 3. ЗамечаниеЗаметим, что высоты треугольника могут не пересекаться.
- 4. Теорема 2Медианы треугольника пересекаются в одной точке
- 5. Вопрос 1Какие точки относятся к числу замечательных
- 6. Вопрос 2Всегда ли высоты треугольника пересекаются? Ответ: Нет. Высоты тупоугольного треугольника не пересекаются.
- 7. Вопрос 3Как называется точка пересечения высот?Ответ: Ортоцентр.
- 8. Вопрос 4Как называется точка пересечения медиан?Ответ: Центроид.
- 9. Вопрос 5В каком отношении делятся медианы треугольника точкой их пересечения?Ответ: 2:1, считая от вершин.
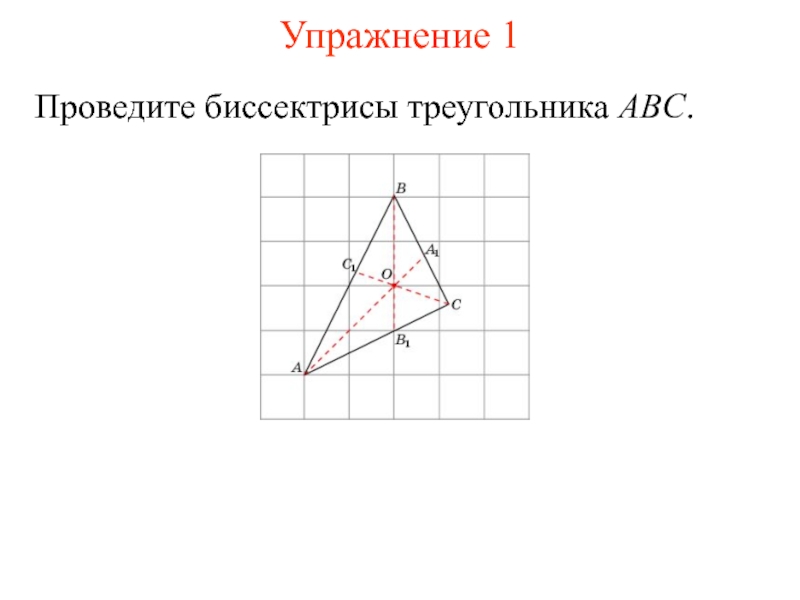
- 10. Упражнение 1Проведите биссектрисы треугольника ABC.
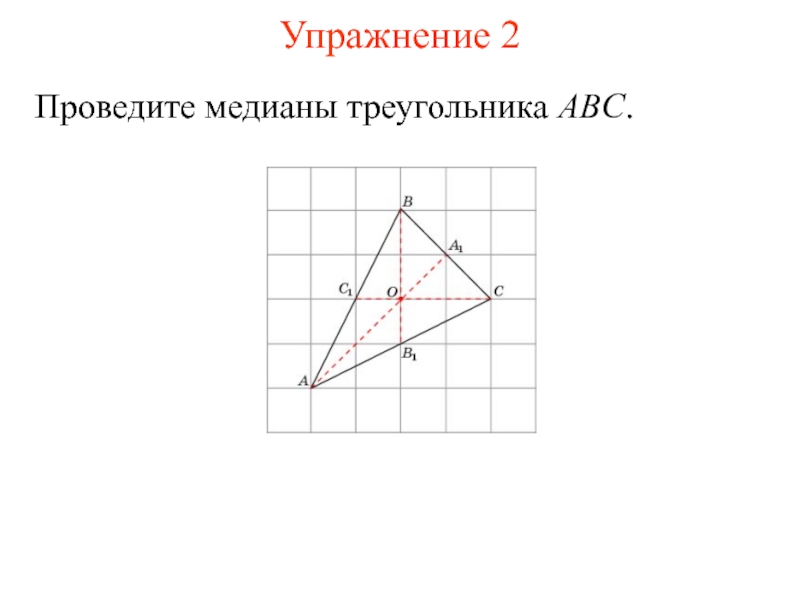
- 11. Упражнение 2Проведите медианы треугольника ABC.
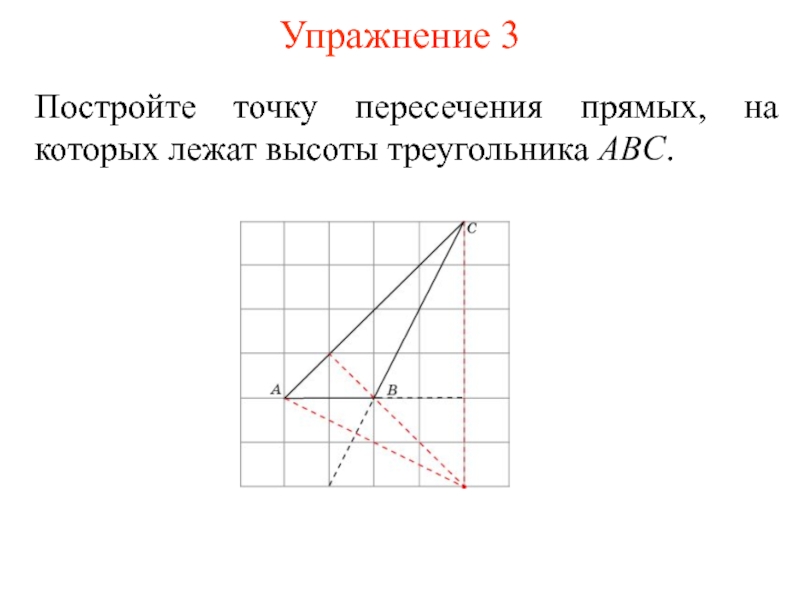
- 12. Упражнение 3Постройте точку пересечения прямых, на которых лежат высоты треугольника ABC.
- 13. Упражнение 4Может ли точка пересечения биссектрис треугольника находиться вне этого треугольника?Ответ: Нет.
- 14. Упражнение 5Может ли точка пересечения медиан треугольника находиться вне этого треугольника?Ответ: Нет.
- 15. Упражнение 6Может ли точка пересечения высот или их продолжений находиться вне этого треугольника?Ответ: Да.
- 16. Упражнение 7Ответ: Да, у прямоугольного треугольника.Может ли вершина треугольника быть точкой пересечения его высот?
- 17. Упражнение 8Где находится точка пересечения серединных перпендикуляров
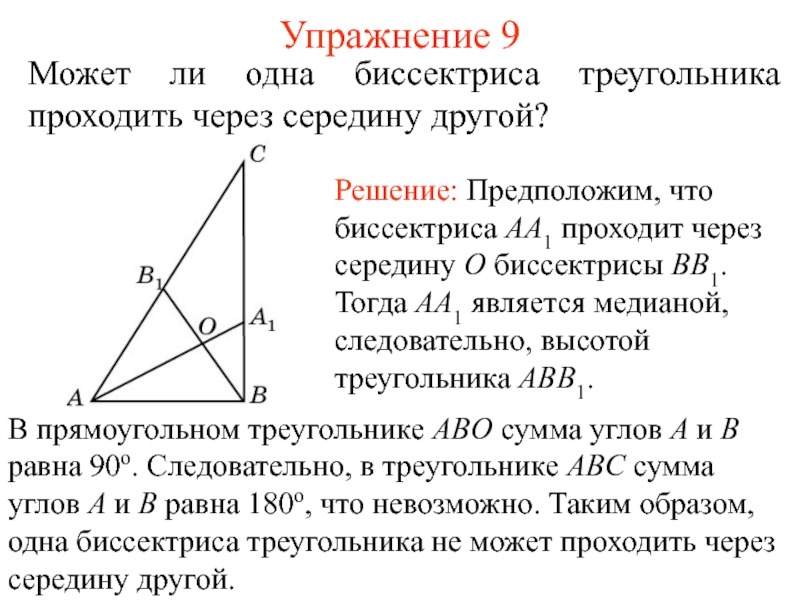
- 18. Упражнение 9Может ли одна биссектриса треугольника проходить через середину другой?
- 19. Упражнение 10К какой из сторон треугольника ближе расположен центр описанной окружности? Ответ: К большей стороне.
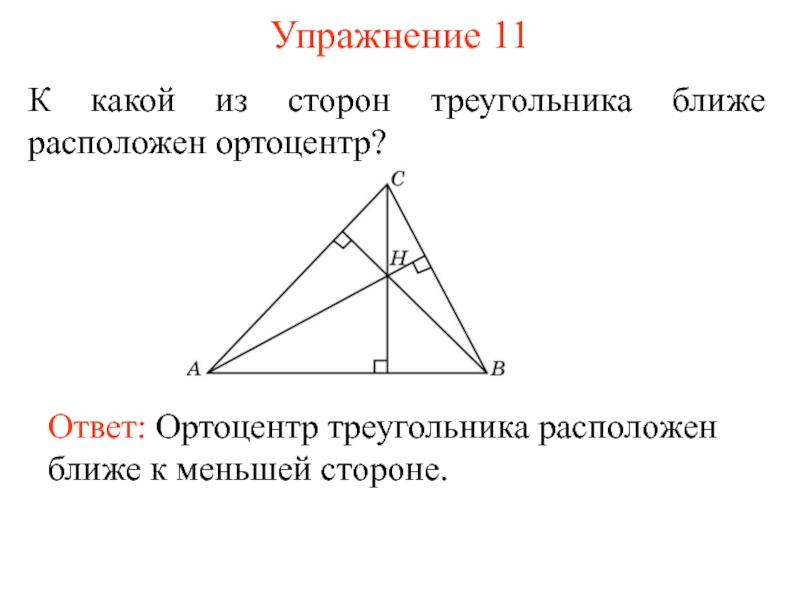
- 20. Упражнение 11К какой из сторон треугольника ближе
- 21. Упражнение 12К какой из вершин треугольника ближе
- 22. Упражнение 13Углы В и С треугольника АВС
- 23. Упражнение 14Биссектрисы АА1 и ВВ1 треугольника АВС пересекаются
- 24. Упражнение 15Биссектрисы АА1 и ВВ1 треугольника АВС пересекаются
- 25. Упражнение 16Углы треугольника АВС равны соответственно 40о,
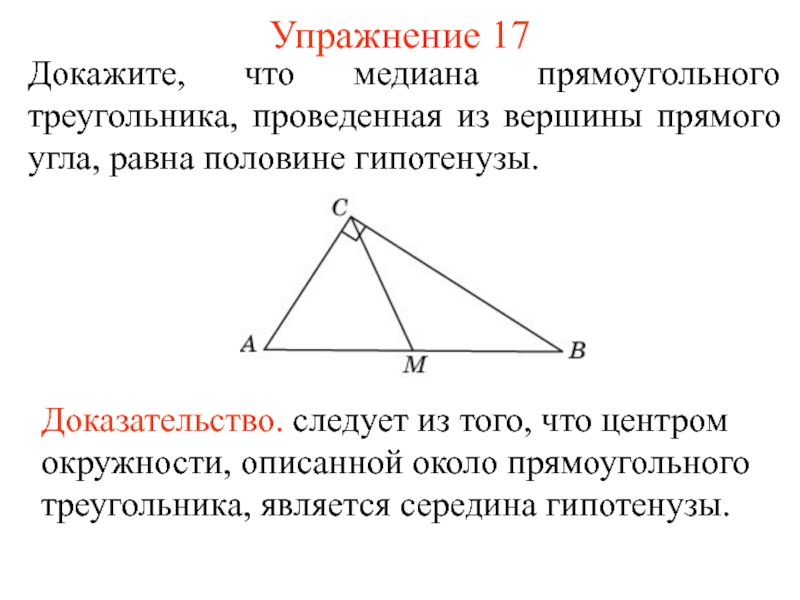
- 26. Упражнение 17Докажите, что медиана прямоугольного треугольника, проведенная
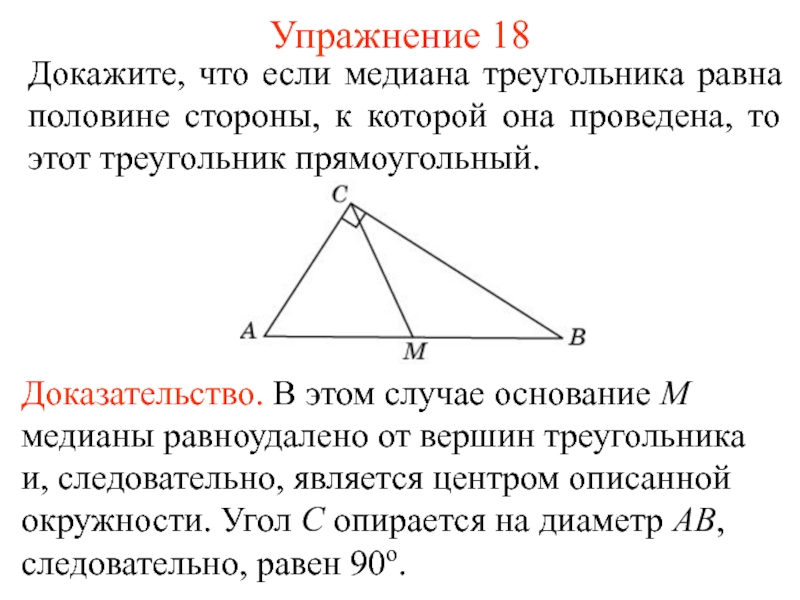
- 27. Упражнение 18Докажите, что если медиана треугольника равна
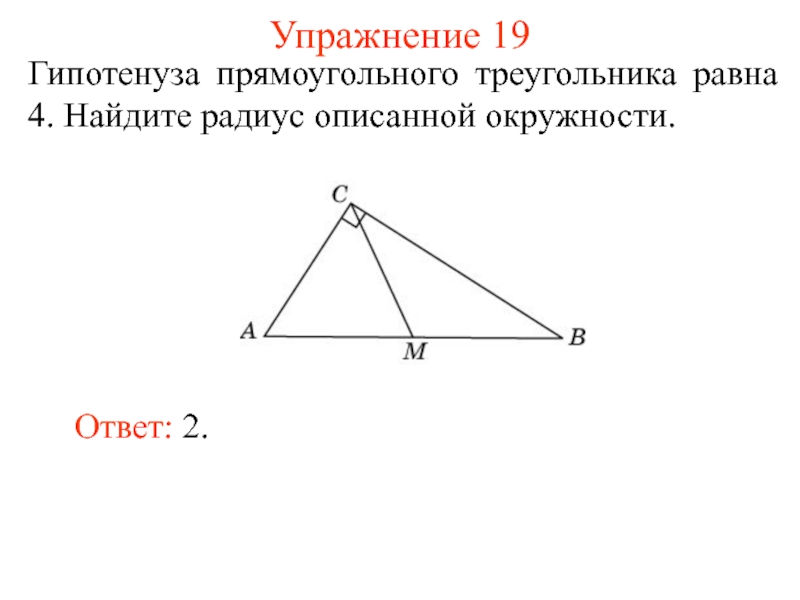
- 28. Упражнение 19Гипотенуза прямоугольного треугольника равна 4. Найдите радиус описанной окружности. Ответ: 2.
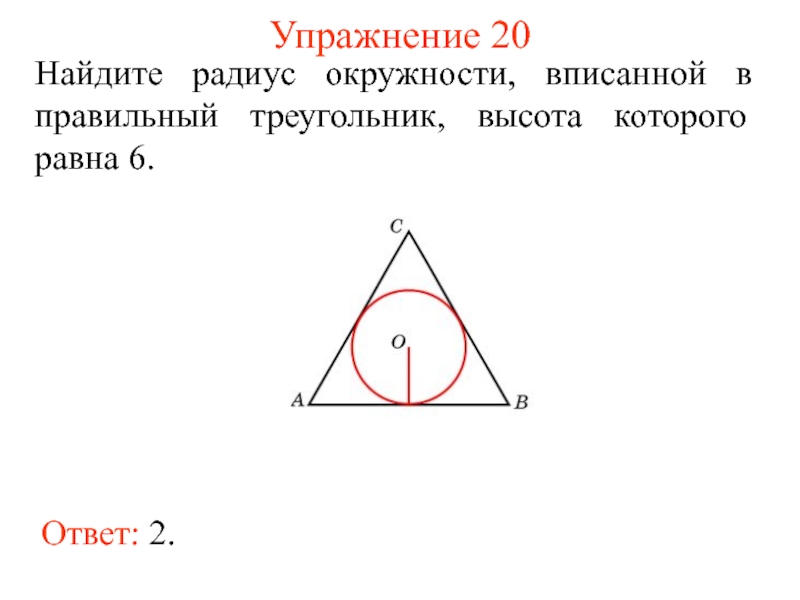
- 29. Упражнение 20Ответ: 2. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.
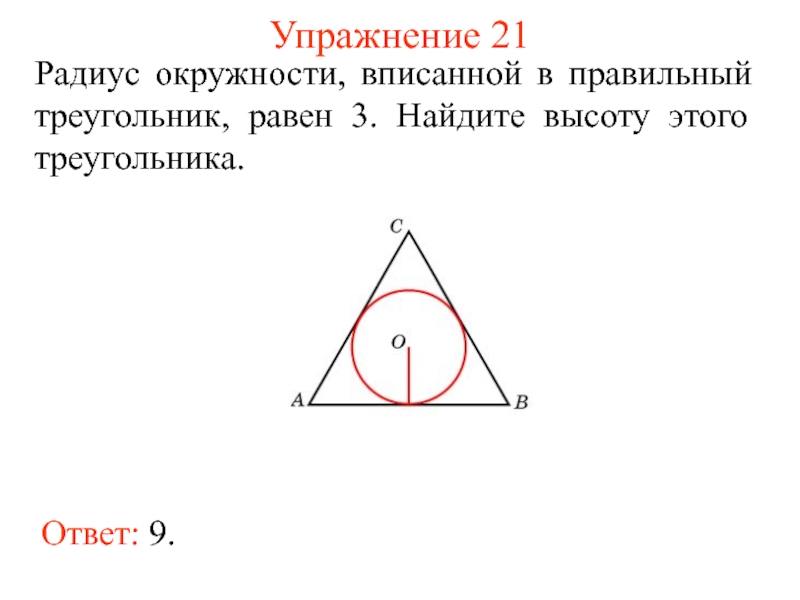
- 30. Упражнение 21Ответ: 9. Радиус окружности, вписанной в правильный треугольник, равен 3. Найдите высоту этого треугольника.
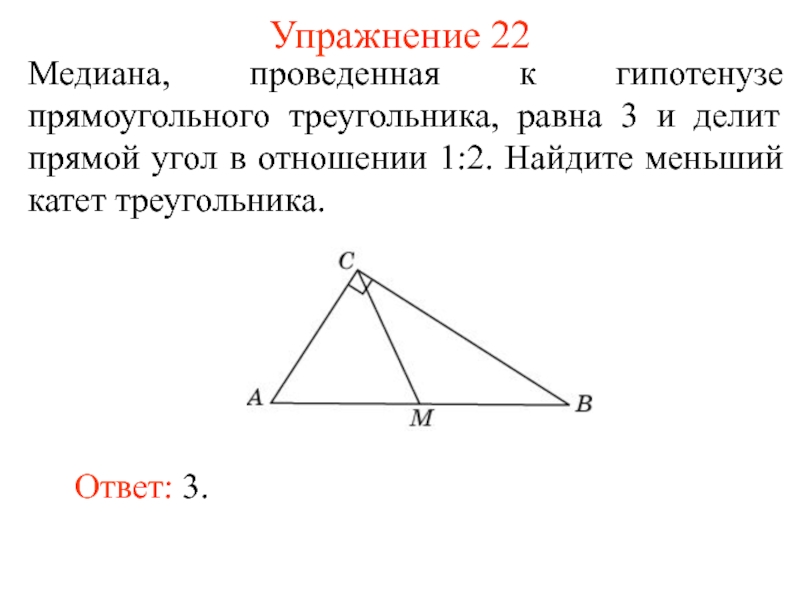
- 31. Упражнение 22Медиана, проведенная к гипотенузе прямоугольного треугольника,
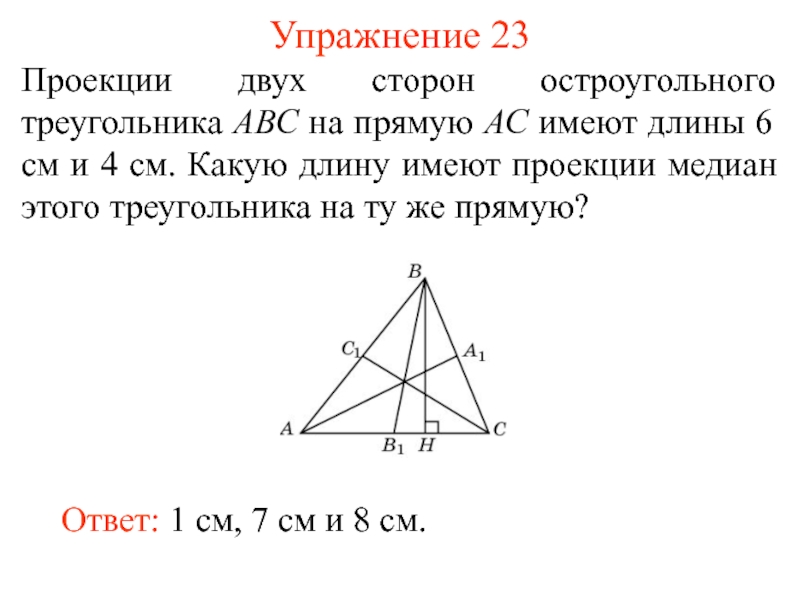
- 32. Упражнение 23Проекции двух сторон остроугольного треугольника АВС
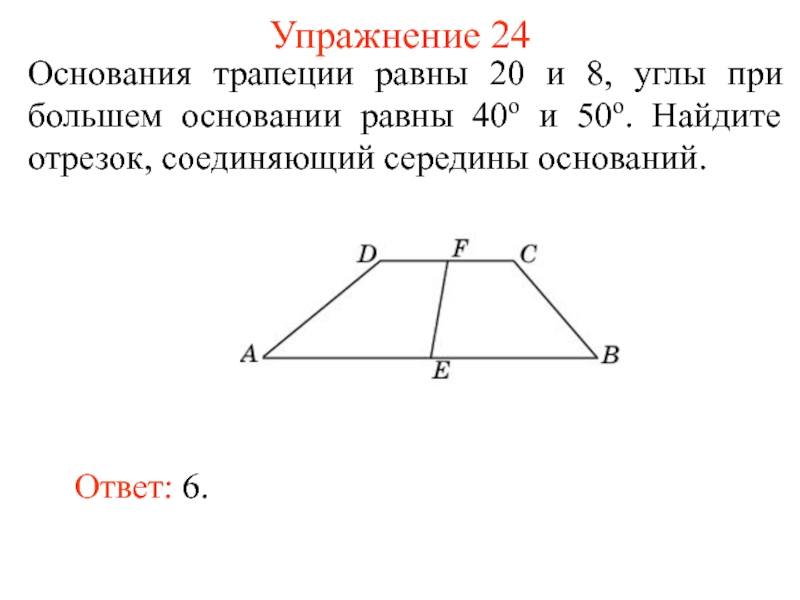
- 33. Упражнение 24Основания трапеции равны 20 и 8,
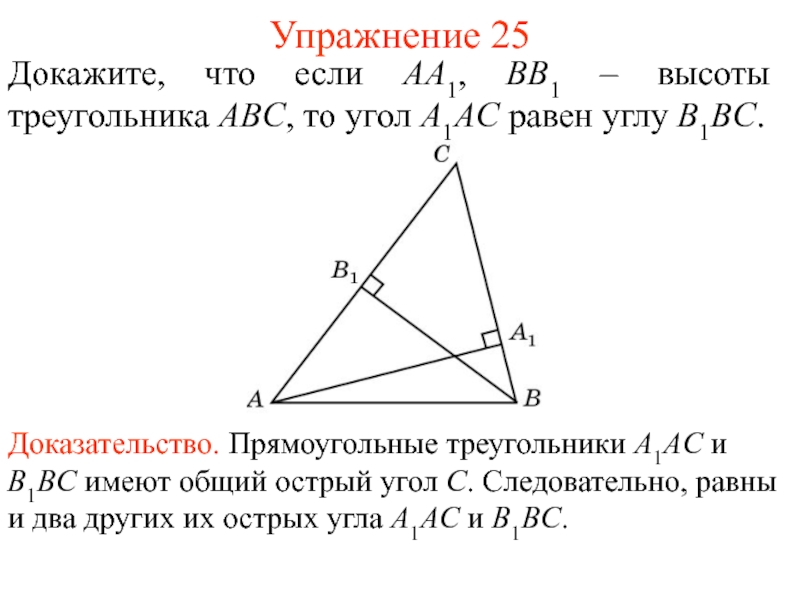
- 34. Упражнение 25Докажите, что если AA1, BB1 –
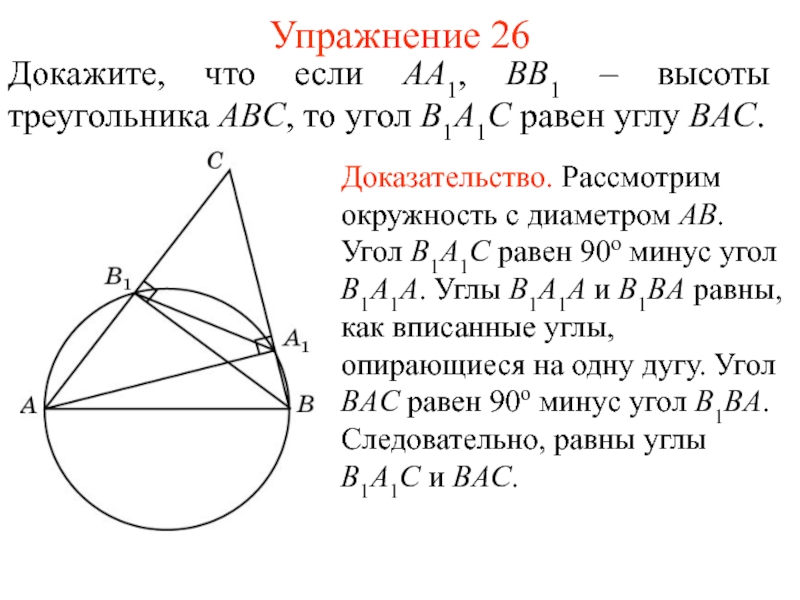
- 35. Упражнение 26Докажите, что если AA1, BB1 –
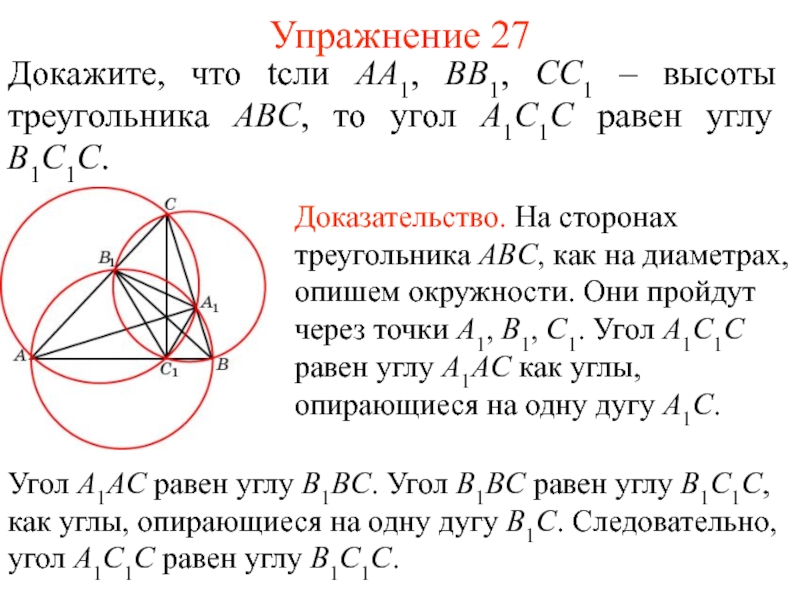
- 36. Упражнение 27Докажите, что tсли AA1, BB1, CC1
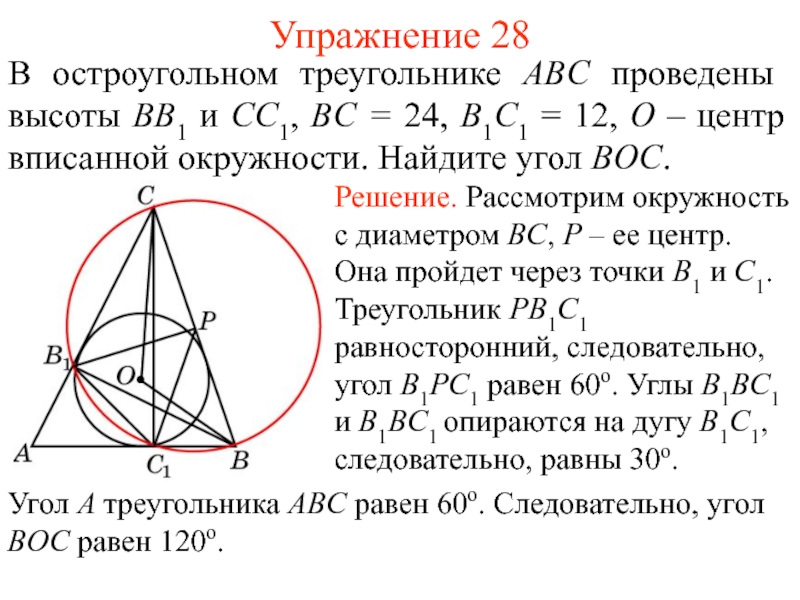
- 37. Упражнение 28В остроугольном треугольнике ABC проведены высоты
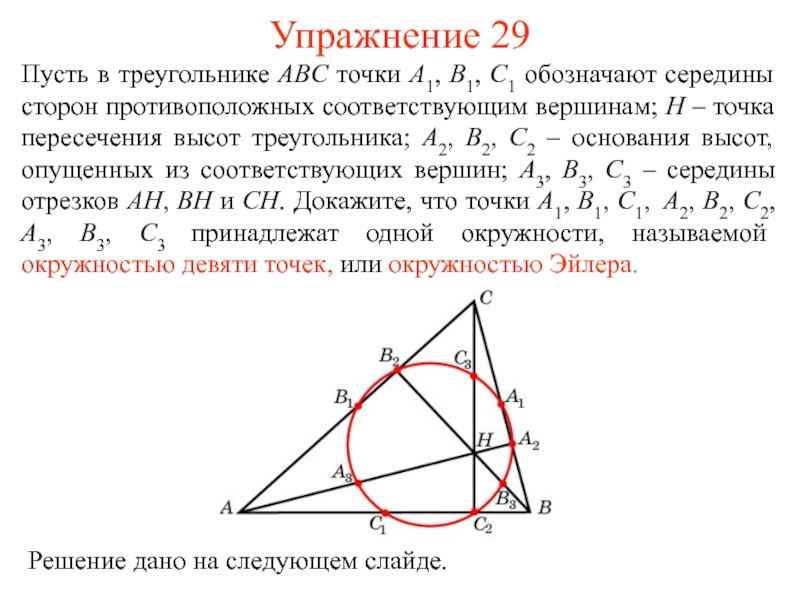
- 38. Упражнение 29Пусть в треугольнике ABC точки A1,
- 39. Решение Проведем окружность через точки C1, C2,
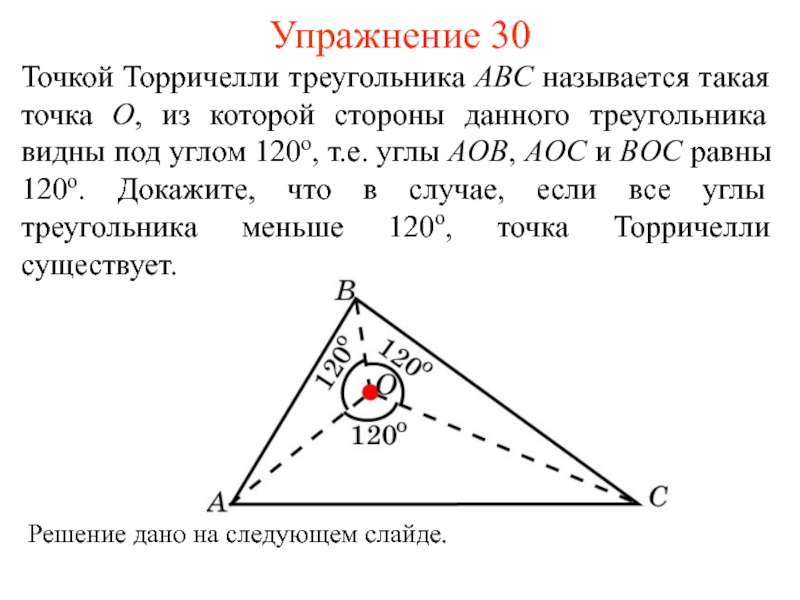
- 40. Упражнение 30Точкой Торричелли треугольника ABC называется такая
- 41. РешениеАналогично, на стороне BC треугольника ABC построим
- 42. Скачать презентанцию
Слайды и текст этой презентации
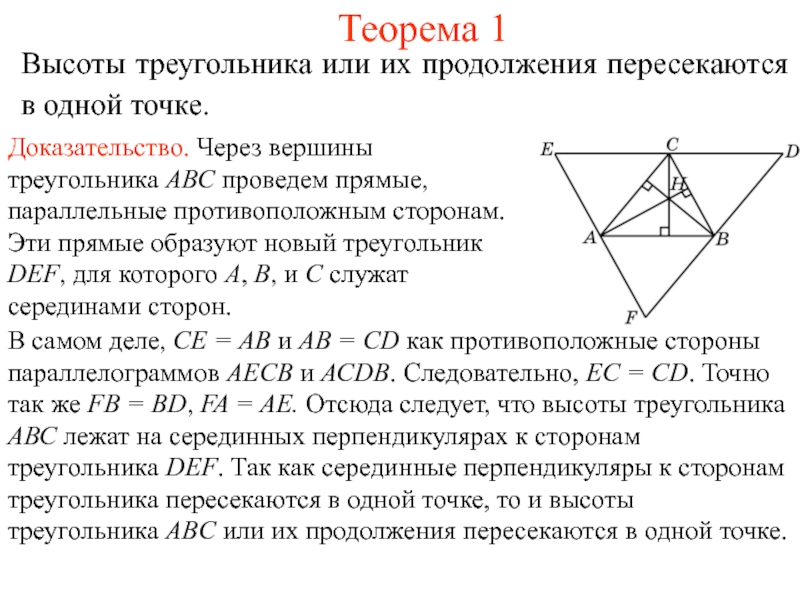
Слайд 2Теорема 1
Высоты треугольника или их продолжения пересекаются в одной точке.
В самом деле, СЕ = АВ и АВ = СD
как противоположные стороны параллелограммов АЕСВ и АСDB. Следовательно, ЕС = СD. Точно так же FB = BD, FA = AE. Отсюда следует, что высоты треугольника АВС лежат на серединных перпендикулярах к сторонам треугольника DEF. Так как серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, то и высоты треугольника ABC или их продолжения пересекаются в одной точке. Слайд 3Замечание
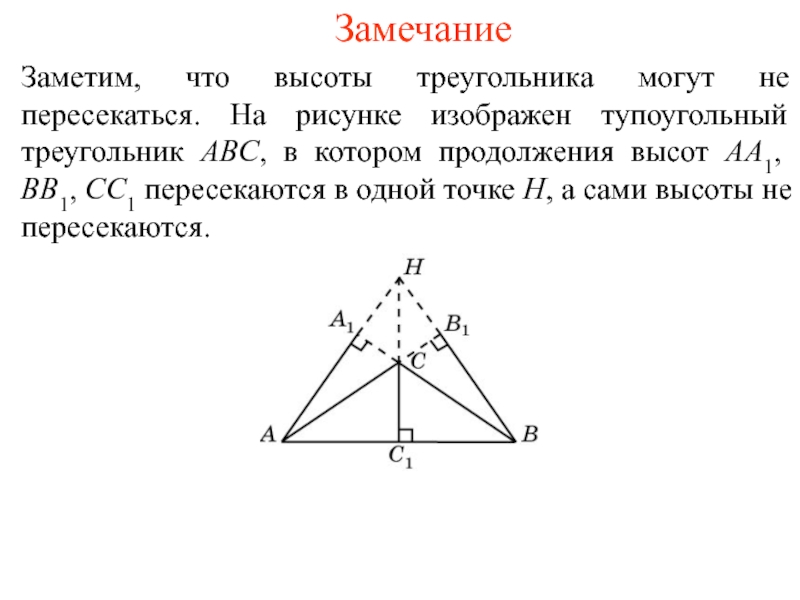
Заметим, что высоты треугольника могут не пересекаться. На рисунке изображен
тупоугольный треугольник ABC, в котором продолжения высот AA1, BB1, CC1
пересекаются в одной точке H, а сами высоты не пересекаются.Слайд 4Теорема 2
Медианы треугольника пересекаются в одной точке и делятся в
этой точке в отношении 2 : 1, считая от вершин.
Треугольники
HGO и EDO равны (по второму признаку равенства треугольников). Следовательно, HO = OE и GO = OD. Таким образом, имеем AG = GO = OD, BH = HO = OE, т.е. медианы АD и BE в точке пересечения делятся в отношении 2:1, считая от соответствующей вершины. Медиана, проведенная из вершины С, также должна делить медиану АD в отношении 2:1. Следовательно, она будет проходить через точку О, т.е. все три медианы будут пересекаться в одной точке. Слайд 5Вопрос 1
Какие точки относятся к числу замечательных точек в треугольнике?
Ответ: К числу замечательных точек треугольника относятся: а) точка пересечения
биссектрис; б) точка пересечения серединных перпендикуляров сторон; в) точка пересечения высот или их продолжений; г) точка пересечения медиан.Слайд 6Вопрос 2
Всегда ли высоты треугольника пересекаются?
Ответ: Нет. Высоты тупоугольного
треугольника не пересекаются.
Слайд 9Вопрос 5
В каком отношении делятся медианы треугольника точкой их пересечения?
Ответ:
2:1, считая от вершин.
Слайд 13Упражнение 4
Может ли точка пересечения биссектрис треугольника находиться вне этого
треугольника?
Ответ: Нет.
Слайд 14Упражнение 5
Может ли точка пересечения медиан треугольника находиться вне этого
треугольника?
Ответ: Нет.
Слайд 15Упражнение 6
Может ли точка пересечения высот или их продолжений находиться
вне этого треугольника?
Ответ: Да.
Слайд 16Упражнение 7
Ответ: Да, у прямоугольного треугольника.
Может ли вершина треугольника быть
точкой пересечения его высот?
Слайд 17Упражнение 8
Где находится точка пересечения серединных перпендикуляров для: а) прямоугольного
треугольника; б) остроугольного треугольника; в) тупоугольного треугольника?
Ответ: а) В середине
гипотенузы; б) внутри треугольника;
в) вне треугольника.
Слайд 19Упражнение 10
К какой из сторон треугольника ближе расположен центр описанной
окружности?
Ответ: К большей стороне.
Слайд 20Упражнение 11
К какой из сторон треугольника ближе расположен ортоцентр?
Ответ: Ортоцентр
треугольника расположен ближе к меньшей стороне.
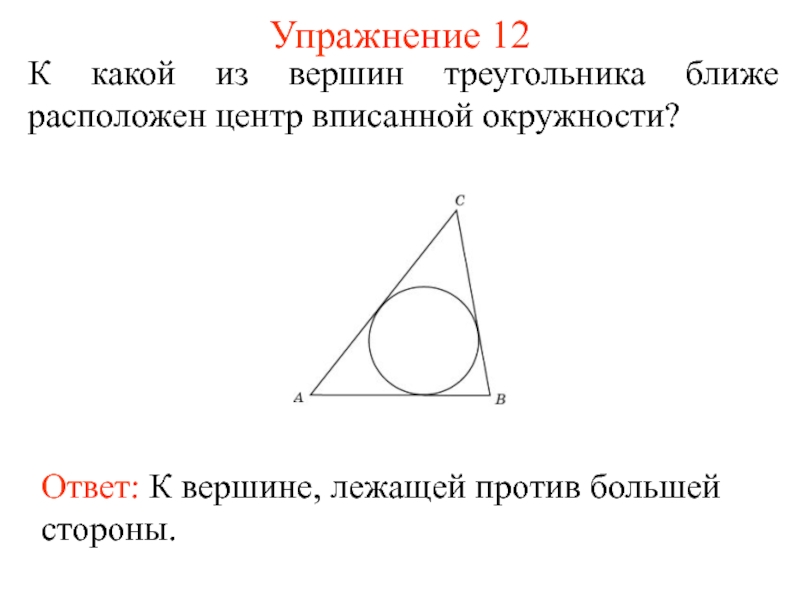
Слайд 21Упражнение 12
К какой из вершин треугольника ближе расположен центр вписанной
окружности?
Ответ: К вершине, лежащей против большей стороны.
Слайд 22Упражнение 13
Углы В и С треугольника АВС равны соответственно 10о
и 100о. Найдите углы ВОС и СОА, где О -
центр описанной окружности.Ответ: 140о, 20о.
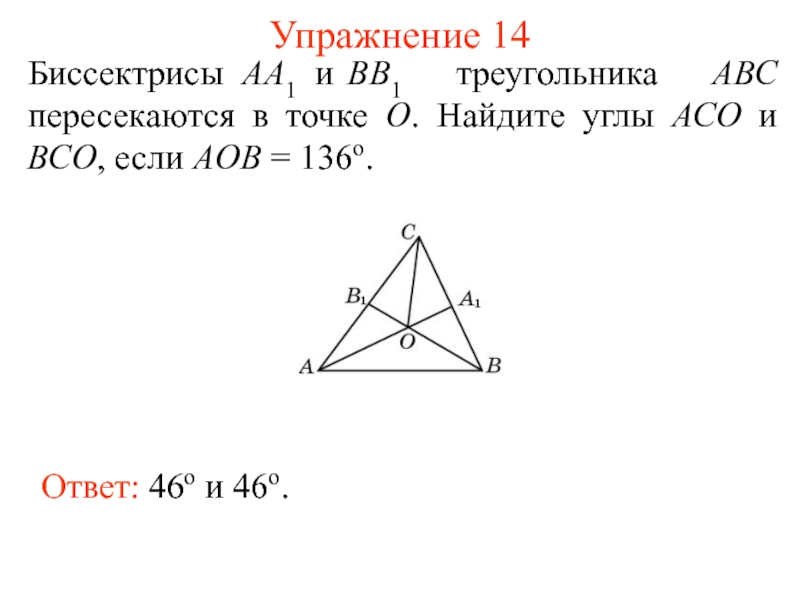
Слайд 23Упражнение 14
Биссектрисы АА1 и ВВ1 треугольника АВС пересекаются в точке О.
Найдите углы АСО и ВСО, если AOB = 136о.
Ответ:
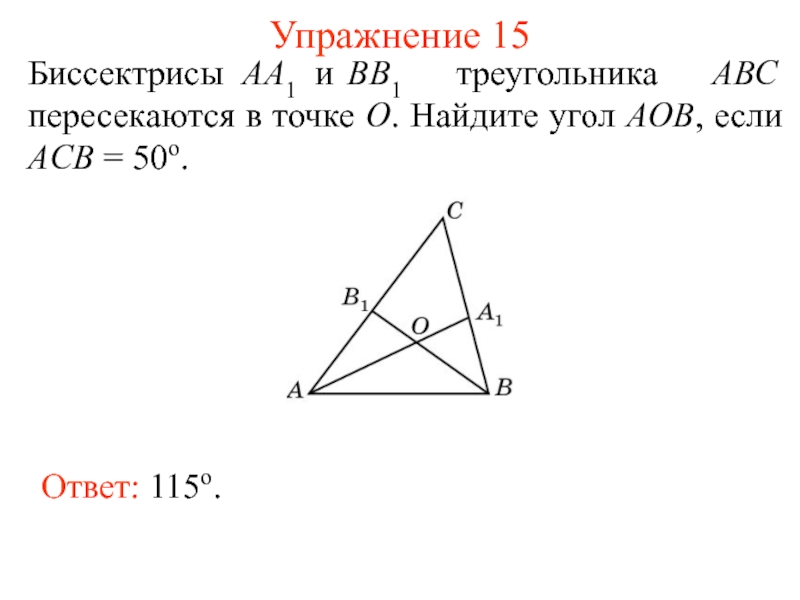
46о и 46о. Слайд 24Упражнение 15
Биссектрисы АА1 и ВВ1 треугольника АВС пересекаются в точке О.
Найдите угол АOB, если ACB = 50о.
Ответ: 115о.
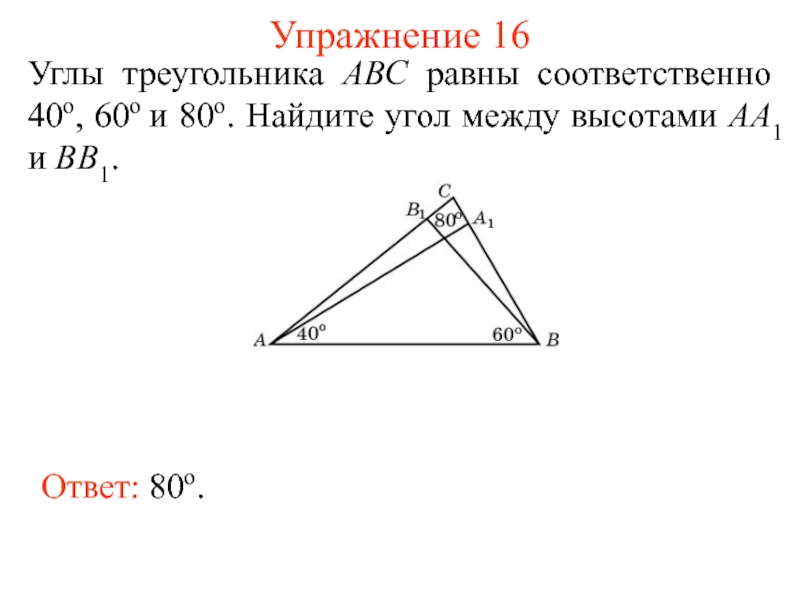
Слайд 25Упражнение 16
Углы треугольника АВС равны соответственно 40о, 60о и 80о.
Найдите угол между высотами АA1 и BB1.
Ответ: 80о.
Слайд 26Упражнение 17
Докажите, что медиана прямоугольного треугольника, проведенная из вершины прямого
угла, равна половине гипотенузы.
Доказательство. следует из того, что центром
окружности, описанной около прямоугольного треугольника, является середина гипотенузы. Слайд 27Упражнение 18
Докажите, что если медиана треугольника равна половине стороны, к
которой она проведена, то этот треугольник прямоугольный.
Доказательство. В этом
случае основание M медианы равноудалено от вершин треугольника и, следовательно, является центром описанной окружности. Угол C опирается на диаметр AB, следовательно, равен 90о. Слайд 28Упражнение 19
Гипотенуза прямоугольного треугольника равна 4. Найдите радиус описанной окружности.
Ответ: 2.
Слайд 29Упражнение 20
Ответ: 2.
Найдите радиус окружности, вписанной в правильный треугольник,
высота которого равна 6.
Слайд 30Упражнение 21
Ответ: 9.
Радиус окружности, вписанной в правильный треугольник, равен
3. Найдите высоту этого треугольника.
Слайд 31Упражнение 22
Медиана, проведенная к гипотенузе прямоугольного треугольника, равна 3 и
делит прямой угол в отношении 1:2. Найдите меньший катет треугольника.
Ответ: 3.
Слайд 32Упражнение 23
Проекции двух сторон остроугольного треугольника АВС на прямую АС
имеют длины 6 см и 4 см. Какую длину имеют
проекции медиан этого треугольника на ту же прямую?Ответ: 1 см, 7 см и 8 см.
Слайд 33Упражнение 24
Основания трапеции равны 20 и 8, углы при большем
основании равны 40о и 50о. Найдите отрезок, соединяющий середины оснований.
Ответ:
6.Слайд 34Упражнение 25
Докажите, что если AA1, BB1 – высоты треугольника ABC,
то угол A1AC равен углу B1BC.
Доказательство. Прямоугольные треугольники A1AC
и B1BC имеют общий острый угол C. Следовательно, равны и два других их острых угла A1AC и B1BC. Слайд 35Упражнение 26
Докажите, что если AA1, BB1 – высоты треугольника ABC,
то угол B1A1C равен углу BAC.
Слайд 36Упражнение 27
Докажите, что tсли AA1, BB1, CC1 – высоты треугольника
ABC, то угол A1C1C равен углу B1C1C.
Слайд 37Упражнение 28
В остроугольном треугольнике ABC проведены высоты BB1 и CC1,
BC = 24, B1C1 = 12, O – центр вписанной
окружности. Найдите угол BOC.Слайд 38Упражнение 29
Пусть в треугольнике ABC точки A1, B1, C1 обозначают
середины сторон противоположных соответствующим вершинам; H – точка пересечения высот
треугольника; A2, B2, C2 – основания высот, опущенных из соответствующих вершин; A3, B3, C3 – середины отрезков AH, BH и CH. Докажите, что точки A1, B1, C1, A2, B2, C2, A3, B3, C3 принадлежат одной окружности, называемой окружностью девяти точек, или окружностью Эйлера.Решение дано на следующем слайде.
Слайд 39Решение
Проведем окружность через точки C1, C2, C3. Отрезок C1C3
будет ее диаметром. Так как A1C1 – средняя линия треугольника
ABC, то A1C1 || AC. Так как A1C3 – средняя линия треугольника BCH, то A1C3 || BH. Значит, и, следовательно, точка A1 принадлежит этой окружности. Аналогично, Так как A3C3 – средняя линия треугольника AHC, то A3C3 || AC. Так как C1A3 – средняя линия треугольника ABH, то C1A3 || BH. Значит, и, следовательно, точка A3 принадлежит этой окружности.
A1C1A3C3 – прямоугольник и, значит, A1A3 – диаметр окружности. Так как
, то A2 принадлежит окружности. Таким образом, мы доказали, что этой окружности принадлежат точки A1, A2, A3. Аналогично доказывается, что этой окружности принадлежат точки B1, B2, B3.
Слайд 40Упражнение 30
Точкой Торричелли треугольника ABC называется такая точка O, из
которой стороны данного треугольника видны под углом 120о, т.е. углы
AOB, AOC и BOC равны 120о. Докажите, что в случае, если все углы треугольника меньше 120о, точка Торричелли существует.Решение дано на следующем слайде.
Слайд 41Решение
Аналогично, на стороне BC треугольника ABC построим равносторонний треугольник A’BC,
и опишем около него окружность. Из точек соответствующей дуги, отличных
B и C, отрезок BC виден под углом 120о. В случае, когда углы треугольника меньше 120о, эти дуги пересекаются в некоторой внутренней точке O, из которой стороны треугольника ABC видны под углом 120о.На стороне AB треугольника ABC построим равносторонний треугольник ABC', и опишем около него окружность. Отрезок AB стягивает дугу этой окружности величиной 120о. Следовательно, из точек этой дуги, отличных от A и B, отрезок AB виден под углом 120о.