Слайд 1
ЗАЩИТА ОТ ШУМА И ПРИМЕНЕНИЕ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ В КАЧЕСТВЕ ЗВУКОИЗОЛЯЦИОНЫХ
Слайд 2Содержание презентации
1. Защита от шума и применение конструкционных материалов в
качестве изоляционных.
2. Защита от шума и применение конструкционных материалов в
качестве звукоизоляционных.
3. Методы расчёта снижения уровней звукового давления.
4. Звукоизоляция при нормальном и диффузионном падении звуковых волн.
5. Расчет звукоизоляции однослойных металлических перегородок импедансным методом.
6. Расчет звукоизоляции плоскости перегородки по закону упругости
7. Применение конструкционных материалов для звукоизолирующих конструкций.
Слайд 3ЗАЩИТА ОТ ШУМА И ПРИМЕНЕНИЕ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ В КАЧЕСТВЕ ЗВУКОИЗОЛЯЦИОННЫХ.
Физические
характеристики звуковых волн
Технологии производства листовых конструкционных материалов и изделий из
них (прокатка, штамповка и др.) предполагают использование крупных и сложных технологических комплексов, работа которых сопровождается интенсивным шумом. Это в значительной степени осложняет условия труда и отрицательно влияет на работоспособность персонала, обслуживающего технологические комплексы.
Для обеспечения нормальных условий труда на производствах с повышенным уровнем шума необходимо внедрение технических решений, шумозащитных материалов и конструкций, обеспечивающих снижение уровня звукового давления до нормативной величины.
Слайд 4В отличие от акустики архитектурной, изучающей влияние формы и размеров
помещения на условия распространения звука в этих помещениях, или физиологической,
предметом которой является исследование функциональных особенностей слухового аппарата и его устройства, физическая акустика представляет раздел теоретической и экспериментальной физики, занимающейся изучением физических явлений, обуславливающих качественные, характеристики звука и возможные превращения одних видов колебаний в другие (электроакустика).
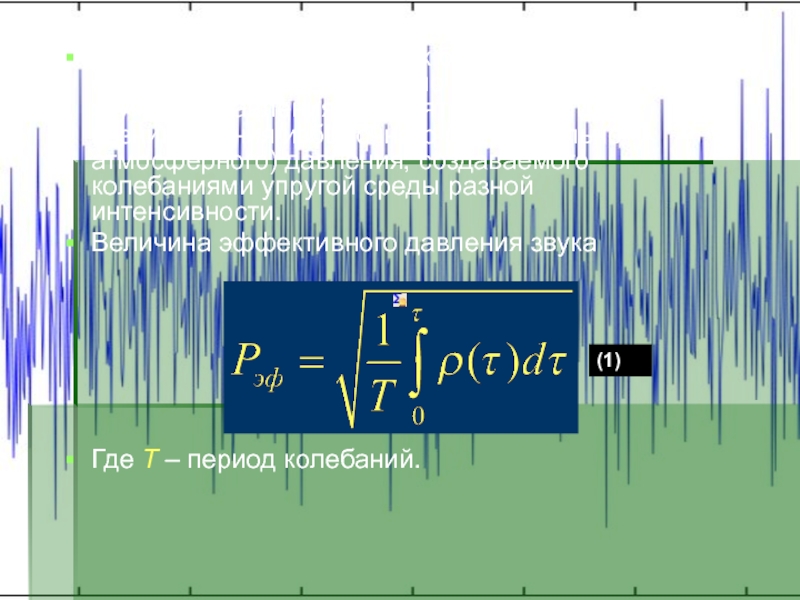
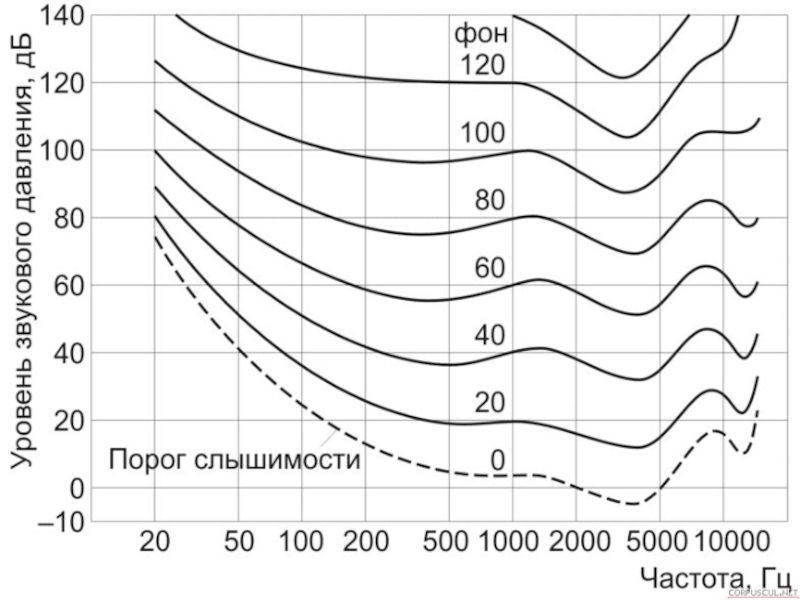
Слайд 5При определении шума как беспорядочного сочетания звуков, разных по частоте
и уровню звукового давления, исходят из условий возникновения избыточного (относительно
атмосферного) давления, создаваемого колебаниями упругой среды разной интенсивности.
Величина эффективного давления звука
Где Т – период колебаний.
(1)
Слайд 6При гармонических (или синусоидальных) колебаниях среды параметром, характеризующим процесс распространения
звуковой волны, является её длина, учитываемая при описании изменения состояния
среды в результате распространения гармонических колебаний. В частности уравнение
Где А – амплитуда волны, ω - циклическая частота, k - волновое число, r- расстояние от источника возбуждения до точки пространства, в которой измеряется свойство среды, (ωτ-kr) – фаза волны, позволяет оценить параметр L (например, давление) среды в точке пространства твердого тела.
(2)
Слайд 7Энергия, переносимая звуковой волной через единицу поверхности среды за конечное
время, характеризует интенсивность (I) звуковой волны Дж/(с*м2)=Вт/м2. В отличие от
сферических L=(A/r)sin(ωτ-kr), цилиндрических L=(A/√r)sin(ωτ-kr) и синусоидальных волн, характеризующихся определенной волновой поверхностью, в жидкостях и газах распространяются только продольные волны, скорость которых для неконденсированных сред (воздуха) зависит от теплоемкости при постоянном давлении, объёме, плотности среды ρ и давлении p что учитывается равенством:
(3)
Слайд 8Для воздуха ϒ=1,41
В идеальном газе фазовая скорость звуковых волн c=√(k/ρ)
Где
ρ – плотность невозмущенной среды, k – модуль объемной упругости
среды, процесс деформации которой для ν ≥ 16 Гц можно считать адиабатическим.
Тогда k=-V(dp/dV) и в адиабатическом процессе рVχ =const (где χ – показатель адиабаты).
С учетом рассмотренных условий скорость распространения звуковой волны в идеальном газе
Где μ- молярная масса газа, Т – абсолютная температура газа, R – универсальная газовая постоянная.
При нормальном атмосферном давлении и 273К скорость распространения звуковой волны в воздухе 331м/с. При р = 101,3 кПа (760мм рт.ст.) и Т – 290К = 340м/с
(4)
Слайд 9Распространение плоской звуковой волны в неконденсированной среде (газах) с разной
скоростью сопровождается изменением звукового давления р, отношение величины которого к
скорости звуковых колебаний ν0=√(I/ρ0c0) =5*10-8 м/с определяется равенством
и не зависит от амплитуды колебаний. Произведение ρ0c0 принято называть удельным акустическим сопротивлением среды (акустическим импендансом), в которой распространяется звуковая волна
(ρ0 = 1,293 (p0/760)(273/T) – плотность воздуха
для воздуха при нормальных условиях ( p = 1,013*105 Па, Т = 290 К ) величина ρ0c0 = 439 кг/(м2с)
(5)
Слайд 10Для определения скорости распространения звуковой волны в конденсированных средах (в
твердых телах или жидкостях) используют уравнения:
- в металлических стержнях
- в
жидкостях
Для определения скорости продольных звуковых волн и твердом материале, поперечные размеры которого значительно превышают длину звуковой волны, распространяющейся в этом материале
Скорость распространения звуковых волн в тонких пластинах
(6)
(7)
(8)
(9)
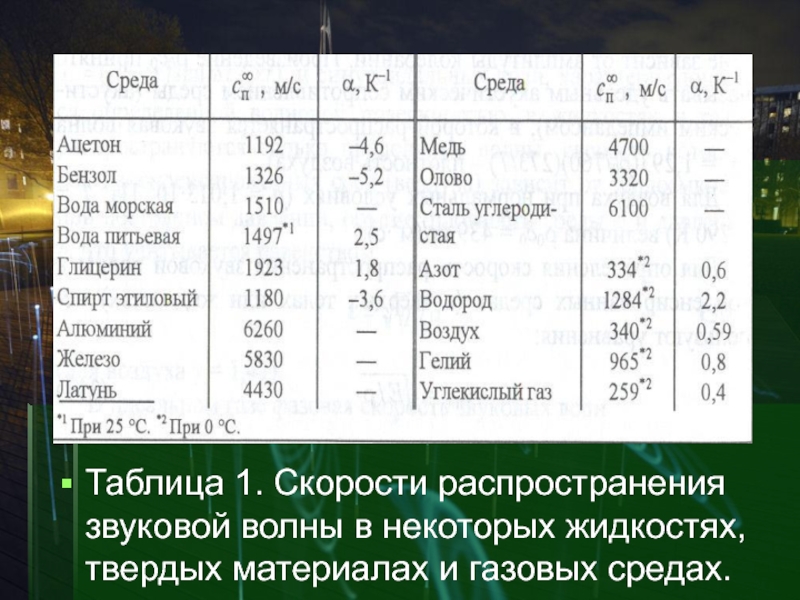
Слайд 11Таблица 1. Скорости распространения звуковой волны в некоторых жидкостях, твердых
материалах и газовых средах.
Слайд 12
Е- модуль нормальной упругости (модуль Юнга), ρ – плотность материала,
μ - коэффициент Пуассона, ϒ=Cp/Cv – изотермическая сжимаемость среды.
В таблице
представлены численные значения скорости распространения звуковой волны в некоторых жидкостях, твердых материалах и газовых средах.
Скорости распространения продольных звуковых волн в некоторых жидкостях, твердых материалах и газовых средах при 20 0C и температурный коэффициент изменения CП∞
Слайд 13Распространение звуковой волны в любой материальной среде сопровождается переносом энергии.
Средняя величина потока энергии, переносимой звуковой волной в единицу времени
через 1см2 поверхности, нормально ориентированной к направлению перемещения волны, называется интенсивностью волны, измеряемой в Вт/м2.
Интенсивностью плоских звуковых волн при их прохождении в материальной среде уменьшается
Где I0 – интенсивность входящей в материальную среду звуковой волны, Ix – интенсивность звуковой волны после прохождения в этой среде расстояния х, α – коэффициент поглощения энергии звуковой волны.
Интенсивность звука и звуковое давление определяется из равенства
(10)
9
Слайд 14Интенсивность звуковой волны – векторная величина, поэтому для диффузного звукового
поля следует использовать другую энергетическую характеристику – плотность звуковой энергии
S. Дж/м3, т.е. количество энергии в единице объема звукового поля.
Плотность звуковой энергии – скалярная величина и может быть представлена отношением среднего значения звуковой энергии в фиксированном объеме к величине этого объема.
Плотность звуковой энергии за время τ≠0 может быть определена как сумма потенциальной энергии и кинетической энергии звуковых волн.
Средняя плотность энергии звуковой волны за период Т
Где Kp– величина звукового давления, ρ – плотность среды, Ѱ – амплитуда скорости распространения волны.
(11)
Слайд 15Мощность W звуковой волны определяется общим количеством энергии, излучаемой источником
в единицу времени. Зависимость между интенсивностью звуковой волны и её
мощностью.
Где F – площадь фронта звуковой волны.
Параметры физической акустики, характеризующие звук, являются функцией времени и определяются разными периодами колебаний и амплитудной зависимостью.
Для гармоничных колебаний сложной формы посредством разных преобразований (например, расположением в ряд Фурье) можно получить более простое их представление в виде дискретных частотных спектров, характеризующих звуковой процесс
(12)
Слайд 16Классификация шумов. Уровни звука в частотных полосах.
При классификации шума, представляющего
собой сочетание звуков разных частот и звуковых давлений исходят из
условий его образования.
Шум, образующийся при работе узлов трения машин и механизмов, в условиях ударной передачи нагрузки элементами технических устройств классифицируют
как механический.
Слайд 17Классификация шумов. Уровни звука в частотных полосах.
Работа инженерно-технических устройств, эксплуатация
которых основана на использовании пара или газа высокого давления с
его периодическим (или постоянным) выведением в окружающую среду сопровождается образованием шума за счёт турбулентного перемешивания движущихся с большой скоростью воздушных потоков. Такой шум принято классифицировать как аэродинамический.
Работа двигателей внутреннего сгорания сопровождается выбросом в окружающую среду продуктов сгорания топлива. Процесс выбросов продуктов сгорания в окружающую среду со сверхзвуковой скоростью носит импульсный характер и сопровождается шумом, который классифицируют как взрывной.
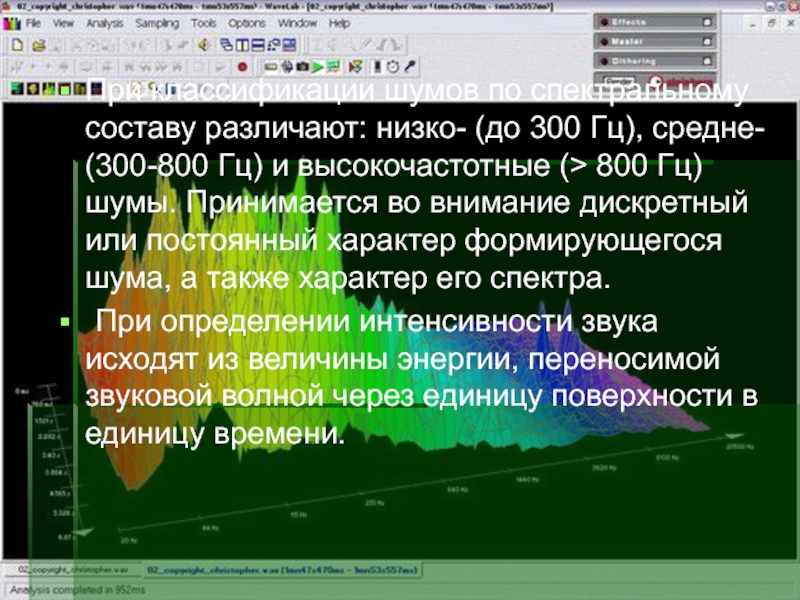
Слайд 18При классификации шумов по спектральному составу различают: низко- (до 300
Гц), средне- (300-800 Гц) и высокочастотные (> 800 Гц) шумы.
Принимается во внимание дискретный или постоянный характер формирующегося шума, а также характер его спектра.
При определении интенсивности звука исходят из величины энергии, переносимой звуковой волной через единицу поверхности в единицу времени.
Слайд 19Для плоской звуковой волны
Где рэф – эффективная величина звукового давления,
Па; с = 340 м/с – скорость звука в воздухе
при атмосферном давлении; ρ – плотность воздуха.
За минимальный уровень интенсивности звука (так называемый порог слышимости) принята величина I = 10-12 Вт/м2. За минимальный уровень звукового давления – величина р0 = 2∙10-5 Па.
Уровень интенсивности звука определяется формулой
(13)
(14)
Слайд 20Зная численные значения звукового давления и акустического импеданса ρ0с0, можно
выразить уровень интенсивности звука через звуковое давление. При этом уровень
звукового давления, дБ,
(15)
Слайд 21Уровни звукового давления на рабочих местах в помещениях цеха или
лаборатории, создаваемые несколькими источниками, не экранирующими друг друга, с уровнями
звукового давления каждого, не отличающимися более чем на 7 дБ (их принято считать источниками равного уровня звукового давления), определяют по формуле
где Lp.1 – уровень звукового давления единичного источника, n – число источников.
Уровни звукового давления на рабочих местах в помещениях цеха или лаборатории, создаваемые несколькими источниками, не экранирующими друг друга, с уровнями звукового давления каждого, не отличающимися более чем на 7 дБ (их принято считать источниками равного уровня звукового давления), определяют по формуле
где Lp.1 – уровень звукового давления единичного источника, n – число источников.
(16)
Слайд 22При удалении источника звука от рабочего места на расстояние r2,
обеспечивающее снижение уровня звукового давления до Lp(r2), можно показать, что
при известном уровне звукового давления Lp(r1) на расстоянии r1 от источника звука величина Lp(r1) определится из равенства
(17)
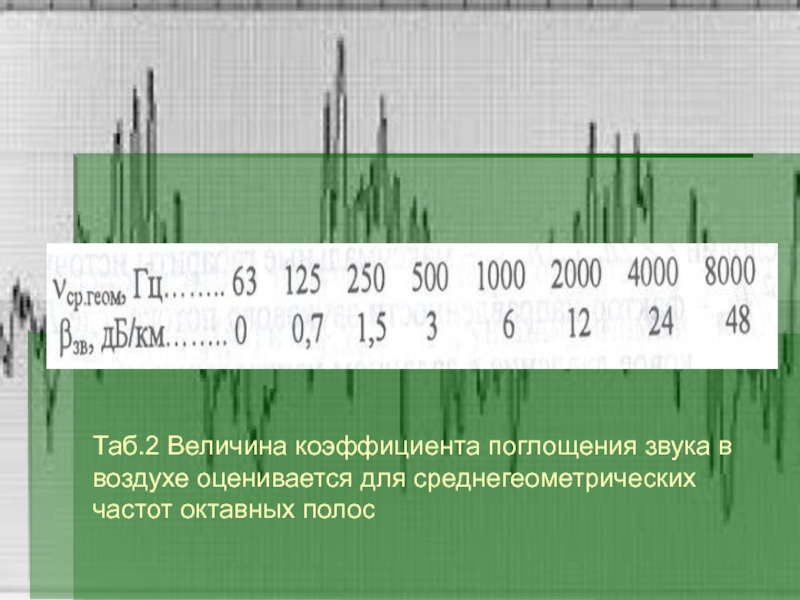
Слайд 23Таб.2 Величина коэффициента поглощения звука в воздухе оценивается для среднегеометрических
частот октавных полос
Слайд 24При условии, что звуковая волна распространяется не в свободном звуковом
поле, а в помещении со строительными конструкциями, оборудованием, необходимо учитывать
поглощение ими звука, а также отражение звуковой волны от поверхностей предметов и оборудования, расположенного в помещении цеха, лаборатории. Частичное поглощение энергии звуковой волны происходит при её падении на поверхность раздела сред. Отношение энергии поглощённой к энергии падающей звуковой волны называется коэффициентом звукопоглощения
(18)
Слайд 25а величина поглощённой энергии звуковой волны поверхностью i при известных
значениях и площади этой поверхности Si
(19)
Слайд 27При наличии в помещении нескольких поверхностей, характеризуемых одинаковой величиной Ѱ,
а также других звукопоглощающих объектов суммарное звуковое поглощение
Где А
– величина звукопоглащения в помещении; n, m – число поглощающих звук поверхностей и объектов в помещении соответственно
(20)
Слайд 28В целом же уровень звукового давления в помещении объемом V
при наличии в нем поглощающих энергию звуковой волны поверхностей определяется
из равенства
Где L – уровень звуковой мощности; k – эмпирический коэффициент (равный для цехов и машинных залов 0,05; для помещений лаборатории без звукопоглащающей облицовки 0,1; со звукоизолирующей облицовкой потолка и стен 0,6. При однородном излучении k=1 для условий r≥2h (h – максимальные габариты источника)
(21)
Слайд 30Ф=Р2/Рср – фактор направленности звукового потока, где Р – звуковое
давление в заданном направлении на расстоянии r от источника, Рср
– усредненное значение звукового давления на расстоянии r от источника при условии распространения звуковой волны от источника в разных направлениях,
Ω - пространственный угол, в который излучается звуковая волна
r – расстояние от источника звуковой волны до точки измерения уровня звукового давления
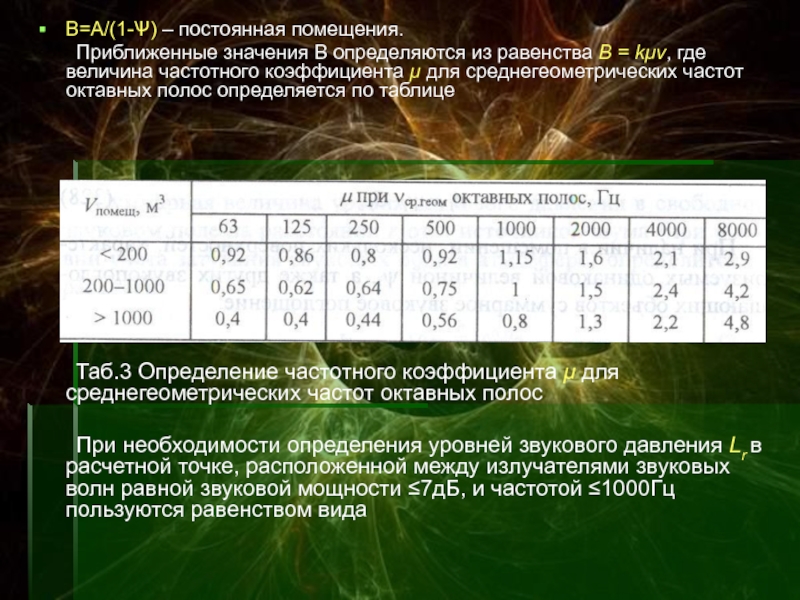
Слайд 31В=А/(1-Ѱ) – постоянная помещения.
Приближенные значения В определяются из равенства В
= kμν, где величина частотного коэффициента μ для среднегеометрических частот
октавных полос определяется по таблице
Таб.3 Определение частотного коэффициента μ для среднегеометрических частот октавных полос
При необходимости определения уровней звукового давления Lr в расчетной точке, расположенной между излучателями звуковых волн равной звуковой мощности ≤7дБ, и частотой ≤1000Гц пользуются равенством вида
Слайд 32 При необходимости определения уровней звукового давления Lr в расчетной точке,
расположенной между излучателями звуковых волн равной звуковой мощности ≤7дБ, и
частотой ≤1000Гц пользуются равенством вида
Где L – октавный уровень звуковой мощности источника, дБ; Н – высота производственного помещения; n=4 при расположении расчетной точки в середине четырех излучателей, равноотстоящих один от другого; m=10; χ=r/H, где r – расстояние от расчетной точки до акустического центра источника.
(22)
Слайд 33Схема размещения источников шума i и k расчетной точки в
плане.
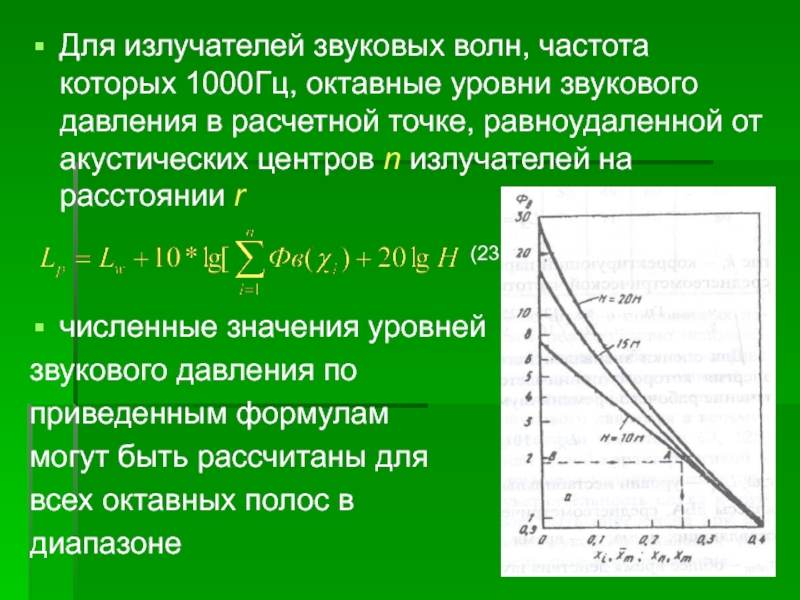
Слайд 34Для излучателей звуковых волн, частота которых 1000Гц, октавные уровни звукового
давления в расчетной точке, равноудаленной от акустических центров n излучателей
на расстоянии r
численные значения уровней
звукового давления по
приведенным формулам
могут быть рассчитаны для
всех октавных полос в
диапазоне
(23)
Слайд 36Методы расчёта снижения уровней звукового давления.
Источниками шума
в исследовательской лаборатории или в цехе могут являться работающие форвакуумные
насосы, ковочные машины, прокатное оборудование и др. Интенсивность шума при эксплуатации технологического оборудования может превышать допустимые значения, что отрицательно влияет на работоспособность персонала, сопровождается быстрой его утомляемостью и потерей слуха.
При оценке интенсивности шума исходят из частотной характеристики уровней звукового давления в интервале значений среднегеометрических частот 53-8000 Гц или уровней интенсивности звука, измеряемых в дБА (где А – корректирующая характеристика измерителя шума, учитывающая чувствитель –
ность слуха к низкочастотным звукам).
Слайд 37Для октавных уровней звукового давления Lр, численные значения уровней звукового
давления в децибелах дБА могут быть определены по формуле
где ki
– корректирующий параметр, величина которого зависит от среднегеометрической частоты звуковой волны:
(24)
Слайд 38Таб.4 Допустимые уровни звука не должны превышать значений L a
и LАэ
Слайд 39Для создания комфортных условий по шуму в помещениях лабораторий и
производственных участков целесообразно использовать различные инженерно-технические решения, обеспечивающие снижение уровней
звукового давления до нормируемых значений.
Величина снижения уровня шума, который оценивается или частотной характеристикой уровней звукового давления в восьмиоктавных полосах со среднегеометрическими частотами 63, 125, 250, 500, 1000, 2000, 4000, 8000 Гц, или одной характеристикой – уровнем звука LA, дБА (А – корректирующая характеристика шумомера, отражающая пониженную чувствительночть слуха к низкочастотным звуковым волнам), может быть определена при известных значениях октавных уровней звукового давления или уровней звука Lдоп при работе технологического оборудования.
Слайд 40При расчёте величины снижения шума ∆L до допустимых нормативных значений
Lдоп, предусмотренных для помещений соответствующего профиля работ, необходимо исходить из
реальных для данного производства уровней звукового давления L и допустимых значений Lдоп.
Расчётная величина ∆L определяется по формуле
где Lдоп определяется по таблице.
(25)
Слайд 41Для расчёта требуемого снижения октавного уровня звукового давления при эксплуатации
оборудования, расположенного в одном производственном помещении и являющегося источником шума
(звуков разной частоты и уровня звукового давления), все источники шума разграничивают на классы в каждой октавной полосе.
Критерием такого разграничения является отличие на 10 дБ уровня звукового давления разного по техническим характеристикам оборудования. К первому классу относят источники шума, для которых выполняются условия Lr ≥ LM - 10, дБ, т. е. когда значения октавных уровней звукового давления Lr в расчётной точке на расстоянии r от акустического центра равны или превышают уменьшенные на 10 дБ значения октавных уровней звукового давления в расчётной точке от наиболее шумного агрегата (источника шума), расположенного на расстоянии М от точки измерения шума.
Слайд 42Ко второму классу источников шума относят машины и агрегаты, октавные
уровни звукового давления Lr которых в расчётной точке находятся в
интервале LM – 20 ≤ Lr < LM – 10 дБ.
К третьему классу источников шума относят машины и агрегаты, для которых выполняются условия: LM - 30 ≤ Lr < LM – 20 дБ и т. д.
Следуя принятым критериям, один и тот же источник шума в разных октавных полосах частот можно отнести к разным классам источников шума.
Слайд 43Исходя из рассмотренных условий, требуемое снижение величины октавного уровня звукового
давления для единичного источника шума первого класса рассчитывают по уравнению
где
Lr, k – величина октавного уровня звукового давления в расчётной точке на расстоянии r от k-того источника шума первого класса; n1 – число источников шума первого класса; L доп – определяется из таблицы.
(26)
Слайд 44Требуемое снижение величины октавного уровня звукового давления от единичных источников
шума второго класса рассчитывают по уравнению
где n2 – число источников
шума второго класса; Lr,k – величина октавного уровня звукового давления в расчетной точке на расстоянии r от k-того источника шума второго класса.
(27)
Слайд 45Требуемое снижение величины уровня звукового давления для единичных источников шума
третьего класса рассчитывают по аналогичной формуле, с той лишь разницей,
что последнее слагаемое в формуле увеличивается на 5.
Для обеспечения допустимых (нормативных) значений по шуму при условии одновременной работы всех машин и агрегатов рекомендуется принимать наибольшее расчетное значение величины снижения уровня звукового давления из полученных для каждой октавы полосы.
Слайд 46Звукоизоляция при нормальном и диффузионном падении звуковых волн.
В конструкциях машин
и механизмов, являющихся источниками шума, должны предусматриваться соответствующие инженерно-технические решения,
задачей которых является снижение шума в источнике его возникновения.
Слайд 47 Одним из таких решений является применение кожухов, перегородок и др.
из звукоизолирующих материалов, характеризующихся соответствующим коэффициентом проницаемости τ или звукоизоляции
R’ :
где I11 – интенсивность звука в падающих на преграду волнах, I21 – интенсивность звука в волнах, прошедших через преграду.
(28)
Слайд 48Звукоизоляцию R, дБ, можно представить разностью соответствующих значений интенсивностей звуковых
волн:
Если это уравнение применимо для условий нормального падения на поверхность
преграды звуковой волны интенсивностью I, то при падении звуковой волны интенсивностью I11 на преграду под углом φ1
(29)
(30)
Слайд 49а для прошедшей через преграду звуковой волны с углом выхода
φ2
где ρс – акустический импеданс (сопротивление среды, в которой распространяется
звуковая волна); ρ1, ρ2 – плотности сред 1 и 2; с1, с2 – скорости распространения звуковой волны в средах 1 и 2.
Если исключить потери звуковой волны за счёт диссипации энергии в твёрдом теле, то эффект звукоизоляции в основном будет обусловлен отражение звуковой волны от поверхности раздела двух сред.
(31)
Слайд 50При оценке звукоизоляции важное значение имеет также величина рассогласования импедансов
– первой и
– второй сред.
Звукоизоляция R границей раздела двух сред при равных значениях акустических импедансов (Z1 = Z2) равна нулю. (При этом принимаются во внимание величины произведений ρ1с1 и ρ2с2, с2.)
Слайд 51Таким образом, принцип рассогласования акустических импедансов определяет эффективность звукоизоляции и
применим для разных сред, образующих контактную пару с общей границей
раздела. Коэффициент звукопоглощения
где
δ - коэффициент рассеяния энергии звуковой волны при известных значениях ε – коэффициента отражения звуковой волны.
(32)
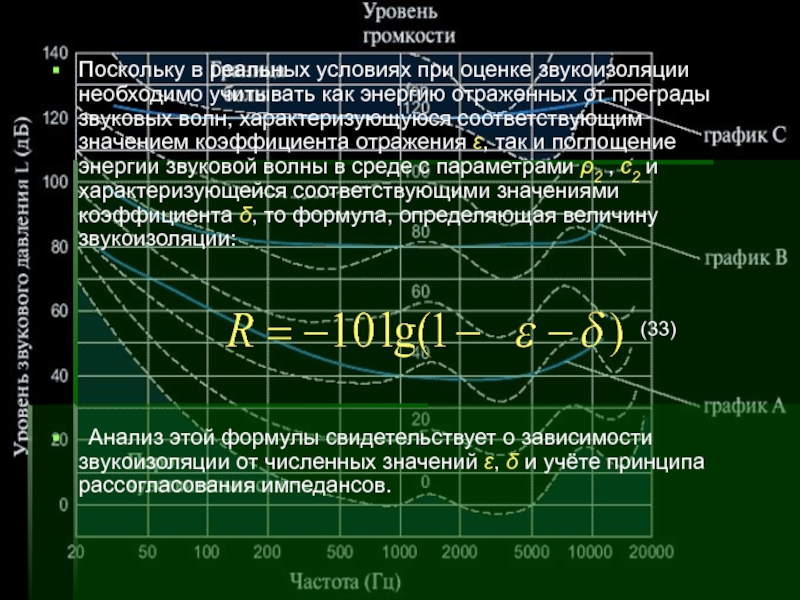
Слайд 52Поскольку в реальных условиях при оценке звукоизоляции необходимо учитывать как
энергию отраженных от преграды звуковых волн, характеризующуюся соответствующим значением коэффициента
отражения ε, так и поглощение энергии звуковой волны в среде с параметрами ρ2 , с2 и характеризующейся соответствующими значениями коэффициента δ, то формула, определяющая величину звукоизоляции:
Анализ этой формулы свидетельствует о зависимости звукоизоляции от численных значений ε, δ и учёте принципа рассогласования импедансов.
(33)
Слайд 53При использовании компактных конструкционных материалов в качестве звукоизолирующих конструкций характерно
малое поглощение ими энергии звуковой волны (δ →0).
Аналогично можно
показать, что для пористых конструкционных материалов характерен высокий уровень диссипации энергии падающей звуковой волны при многократном её отражении от поверхности пористого твёрдого тела, и тогда
(34)
Слайд 54Изложенные сведения реализуются при создании звукоизолирующих конструкций, снижающих шум в
источнике его возникновения.
Для диффузного звукового поля, характеризуемого равномерным распределением плотности
энергии звуковой волны и её интенсивности по всему объёму пространства, звукоизоляция преграды из конструкционного материала
где φп – предельный угол интегрирования; φ – угол падения плоских звуковых волн на поверхность звукоизолирующей преграды; r – радиус полусферы замкнутого объёма, в центре которого расположена звукоизолирующая преграда.
(35)
Слайд 55Расчёт звукоизоляции металлических перегородок по закону массы.
Для условий нормального падения
звуковой волны на поверхность преграды толщиной s, значительно меньшей длины
продольной звуковой волны, при акустическом импедансе материала преграды ρс, существенно большем акустического импеданса среды, окружающей звукоизолирующую преграду, ρ0с0 расчёт звукоизоляции преграды возможен по формуле
где
– круговая частота, с-1; m = ρs – поверхностная масса преграды, кг/м2.
(36)
Слайд 56Анализ формулы показывает, что основным параметром уравнения, влияющим на численные
значения R, является поверхностная масса преграды при ρ0с0 = const.
С увеличением m звукоизоляция перегородки будет увеличиваться, а при увеличении акустического импеданса (ρс > ρ0с0) будет уменьшаться, что характерно для изменения плотности контактной с преградой среды, например, при замене воздушной среды с параметрами ρ0с0 на среду с большими плотностью ρ1 (например, жидкость) и, соответственно с1.
Слайд 57Приближенное значение звукоизоляции перегородки целесообразно в интервале частот ν1 =
100 Гц и ν2 = 3200 Гц.
При ρ0c0 =
428 кг/(м2∙с) – акустический импеданс воздуха, получим
Из анализа следует, что звукоизолирующая способность перегородки определяется её поверхностной массой m и среднегеометрической частотой.
(37)
Слайд 58Применение закона массы для определения звукоизоляции перегородки возможно при выполнении
условий
2νр
резонансная и критическая частоты звукоизолирующей преграды.
Слайд 59Расчет звукоизоляции однослойных металлических перегородок импедансным методом.
Для расчета звукоизоляции
однослойных металлических перегородок из компактных конструкционных материалов, плотность ρ и
модуль E которых одинаковы по всему объему металла, может быть использован импендансный метод для условий нормального падения на перегородку плоских продольных гармонических волн.
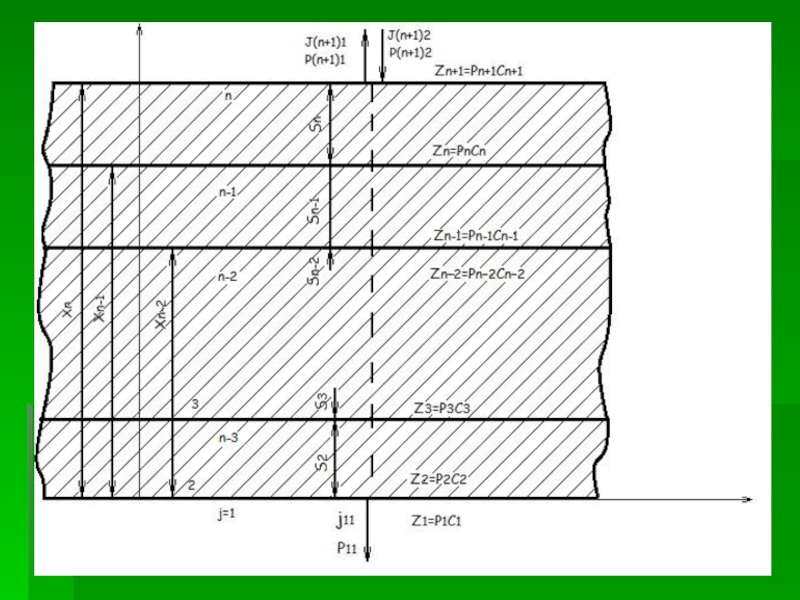
Импедансный метод расчета звукоизоляции однослойных металлических перегородок предполагает также наличие полубесконечных сред с параметрами ρ1с1 и ρ3с3, расположенных по обе стороны плоской однослойной металлической перегородки с параметрами ρ2с2 (ρ – плотность среды кг/м3, с – скорость звука в среде м/с).
Слайд 61Для расчета звукоизоляции однослойной пластины необходимо определить входной импеданс, величина
которого определяется отношением звукового давления p11 в среде с параметрами
ρ1, c1, в которой распространяются звуковые волны, к колебательной скорости волны в другой среде с параметрами p2, c2, имеющей общую границу раздела с первой средой.
Слайд 62Следуя условиям, указанным на рисунке, звуковое давление в слое пластины
толщиной s1 с некоторым приближением (не учитывается iωτ ) будет
определяться равенством
в котором учитывается возможность распространения в слое s2 падающей и отраженной от нижней границы раздела звуковых волн.
(38)
Слайд 63Колебательная скорость определяется аналогично
Где p21 и p22 – звуковые давления
в среде при прохождении в слое падающей и отраженной волны,
х – текущая координата, учитывающая направление и величину распространения волны в слое.
(39)
Слайд 64Из уравнения следует, что p(х) = p21 + p22, при
x=s2
При х=0 величина входного импеданса на верхней (см. рисунок) границе
раздела сред с параметрами p1, c1 и p2, с2
Где
- постоянная распространения звуковой волны в среде с параметрами ρ2, с2 (пластине);
- волновое число слоя.
(40)
(41)
Слайд 65Для практической оценки величины звукоизоляции однослойной звукоизолирующей перегородки рассматривают систему,
состоящей из собственной звукоизолирующей , характеризующейся определенным акустическим, сопротивлением z2=
ρ2с2, а также из распределенной по обе стороны перегородки воздушной среды (см. рис) с параметрами z1=z3=z0= ρ0с0, где z0 – акустический импеданс воздуха.
Слайд 66Если при этом z2>>z0 (что как правило выполняется) β2 =
0, то для тонких пластин входной импеданс
Используя приближенную оценку звукоизоляции
R однослойных преград
(42)
(43)
Слайд 67При известных значениях
можно окончательно получить
откуда следует, что звукоизоляция
металлической пластины при нормальном падении звуковой волны на поверхность пластины
определяется в основном ее поверхностной массой.
(44)
(45)
Слайд 68Расчет звукоизоляции плоскости перегородки по закону упругости
В отличии от звукоизоляции
R тонкой металлической перегородки, величина акустического импенданса z1 который превосходит
численные значения акустического импенданса воздуха z0=p0c0 (т.е. z1>>z0), что обеспечивает возможность применения для оценки R закона массы, величину звукоизоляции для слоистой звукоизоляционной перегородки с параметрами z1=p1c1, z2= p2c2, z3= p3c3 при z1= z3 и z1>> z2 следует рассчитывать по закону упругости
Этот закон применим для слоистых систем, состоящих из разных материалов (например, плотной вакуумной резиновой пластины z2 между стальными пластинами z1).
Слайд 71Так, например, для системы состоящей из трех монослоев с параметрами
p1c1, p2c2 и p3c3, где pc – характеристические импендансы соответствующих
твердых материалов слоистой композиции, величина звукоизоляции
Где s2 – толщина среднего слоя с параметрами p2, c2 ; p – плотность материала слоя, c – скорость распространения звука в материале слоя;
– частота.
(46)
Слайд 72Для p1c1 = p3c3 запишется в виде
Где Kр – модуль
объемной упругости материала слоя толщиной s2.
Анализ равенства показывает, что звукоизоизоляция
слоистой преграды (например, слоистого композита) повышается с увеличением частоты колебаний звуковой волны ω=2πν и акустического импенданса слоя с z1=p1c1 при уменьшении значения модуля объемной упругости Kр материала этого слоя.
(47)
(47)
Слайд 73Вместе с тем равенство применимо для оценки звукоизоляции слоистой перегородки,
в которой толщина слоя s2 имеет ограниченные размеры.
Эти ограничения по
толщине слоя звукоизолирующей перегородки определяются выражением s2 ≤c2/20 πν
Где К2s2 <=0,1 , где К=2πν – волновое число и s2 - толщина слоя, а погрешность оценки R при этих допущениях не превышает 7%, т.е. = 0,6 дБ, что вполне допустимо для практических расчетов звукоизоляционных преград.
Слайд 74Применение конструкционных материалов для звукоизолирующих конструкций.
В промышленной звукоизоляции наиболее широкое
применение находят одностенные металлические конструкции – звукоизолирующие кожухи или экраны
разного исполнения, которые обеспечивают снижение величины звукового давления в помещении при наличии в нем источника шума.
Звукоизолирующие кожухи могут быть изготовлены из стали или алюминиевых сплавов, их внутренняя поверхность облицовывается звукопоглощающим материалом, что значительно повышает их эффективность и эффективность всей
системы звукоизоляции.
Слайд 75Эффективность применения звукоизолирующих кожухов, укрывающих источник шума, оценивается понижением величины
звукового давления:
Где ∆L и ∆Lобл - уменьшение звукового давления
соответственно металлической конструкцией кожуха и звукопоглощающей облицовкой, дБ.
Снижение уровня звукового давления на рабочем месте может быть достигнуто и применением шумозащитных экранов.
(48)
Слайд 76Величина снижения звукового давления при использования шумозащитных экранов определяется из
равенства
Где ω1 = (p1/c1)[1/(2πr2)+4/B1] – плотность звуковой энергии на рабочем
месте, удаленном от источника шума на расстояние r, р – мощность источника шума, Вт; В1 - постоянная помещения, м2; с1 – скорость продольной звуковой волны в воздухе; ω2=4р/(β2с2) – плотность звуковой энергии на рабочем месте после установки экрана (с2 - скорость продольной звуковой волны в материале экрана); β2 – постоянная помещения после установки экрана, м2.
(49)
Слайд 78В промышленной звукоизоляции применяются также стрингерные (состоящие из листового металла,
на поверхности которого закреплены ребра жесткости – стрингеры) и сотовые
конструкции.
Звукоизоляция стрингерных панелей в интервале частот 63 – 8000 Гц может достигать величины 20-30 дБ.
Металлические сотовые конструкции – сотовый заполнитель, распределенный между листовым металлом, эффективно снижает звуковое давление. В зависимости от размера ячейки заполнителя величина звукоизоляции такой конструкции в интервале частот от 63-8000 Гц может достигать 40дБ.
Слайд 79Список использованной литературы
1. Варенков А.Н., Костиков В.И. Химическая экология и
инженерная безопасность металлургических производств: учебное пособие. – М.: «Интермет Инжиниринг»,
2000

































































![ЗАЩИТА ОТ ШУМА И ПРИМЕНЕНИЕ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ В КАЧЕСТВЕ Величина снижения звукового давления при использования шумозащитных экранов определяется из равенстваГде Величина снижения звукового давления при использования шумозащитных экранов определяется из равенстваГде ω1 = (p1/c1)[1/(2πr2)+4/B1] – плотность звуковой](/img/thumbs/39be393e4fdc645019488f358e9299f6-800x.jpg)