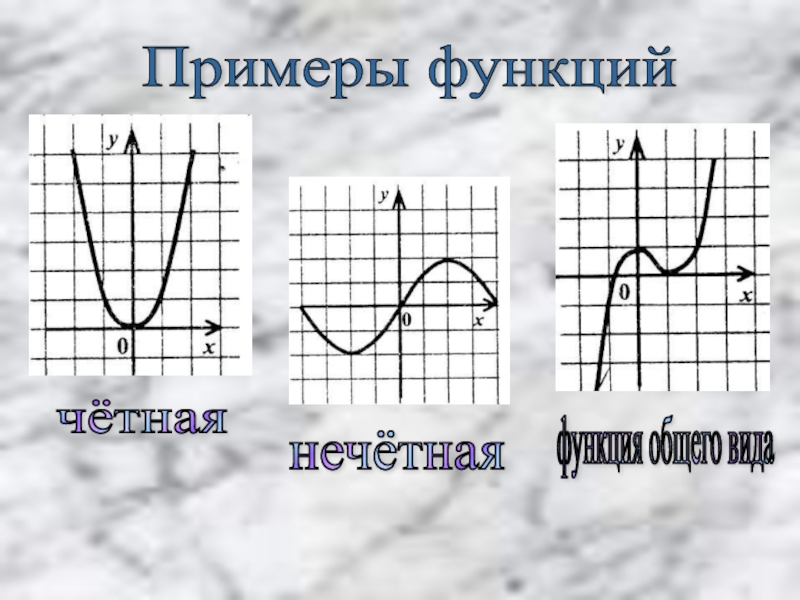
определения симметрична относительно нуля и для любого значения аргумента x
верно равенство g (-x) = - g (x)Чётная функция
Функция y = f(x) называется четной, если область ее определения симметрична относительно нуля и для любого значения аргумента x верно равенство f (-x) = f (x)
Определения





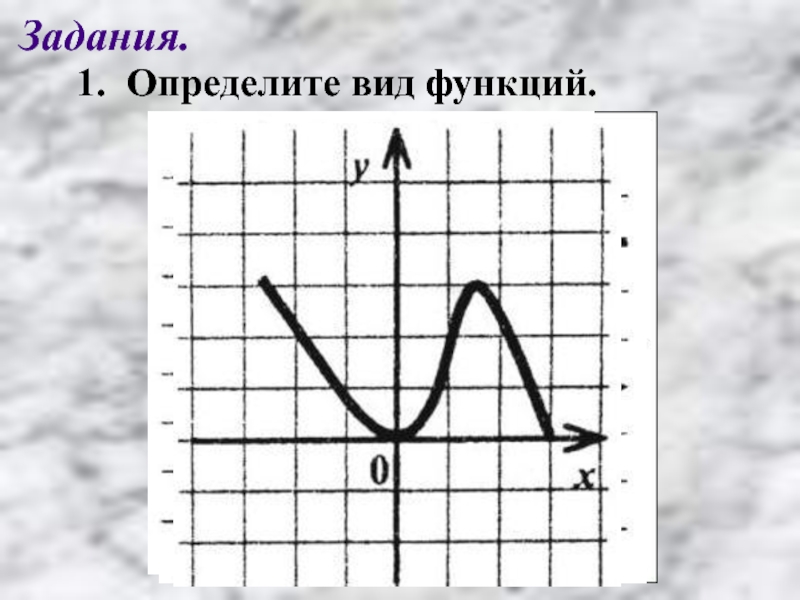
![Чётность, нечётность, периодичность функций 11 класс 2. Дан фрагмент графика четной функции f(х), котораяопределена на [–9; 9]. 2. Дан фрагмент графика четной функции f(х), котораяопределена на [–9; 9]. Достройте график функции f(х) и ответьте](/img/thumbs/08e7c32fb713f349dc4d9a9d1406a309-800x.jpg)


























