Функция. График функции. 7 класс

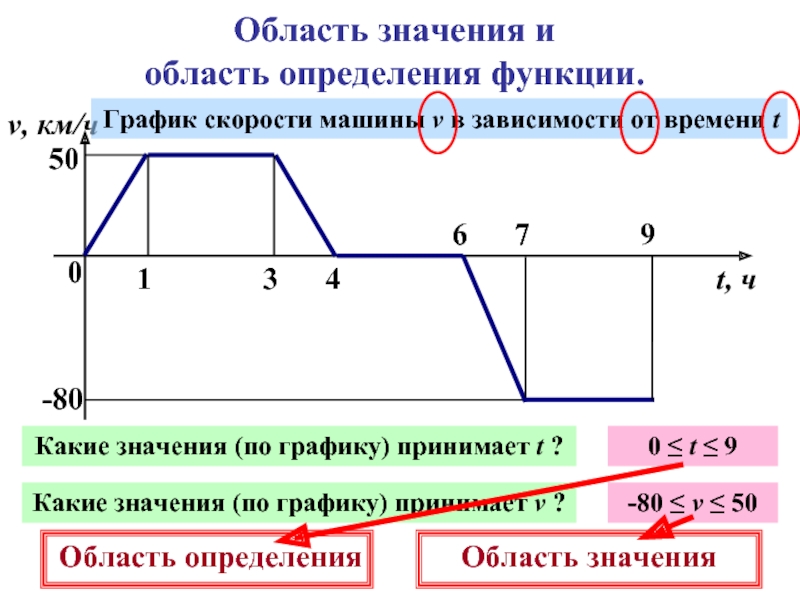
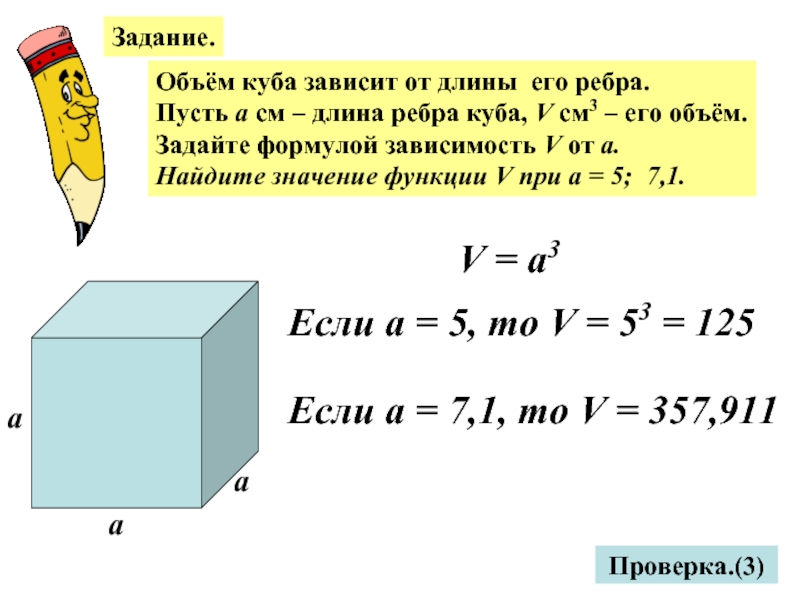
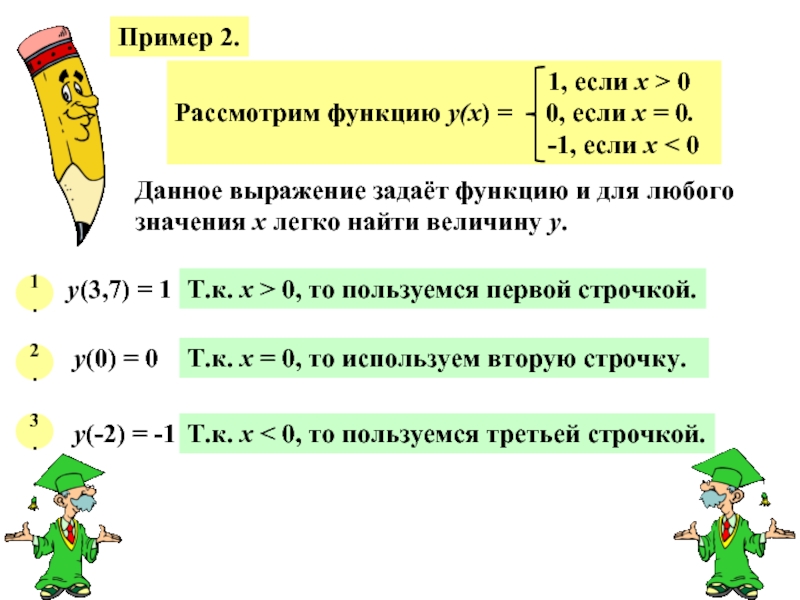
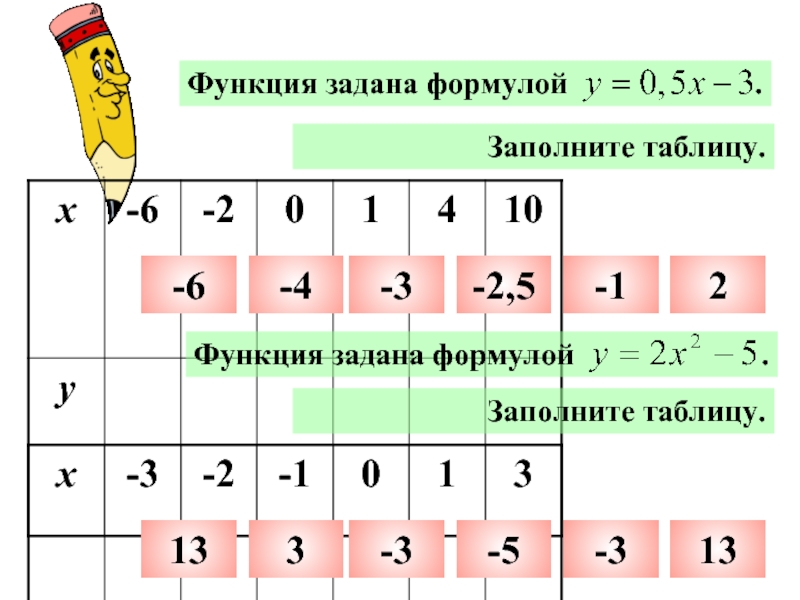
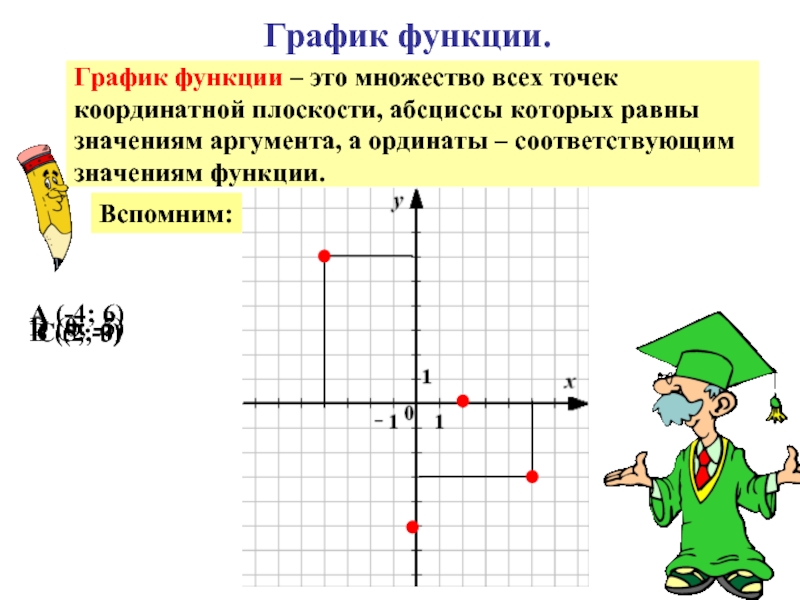
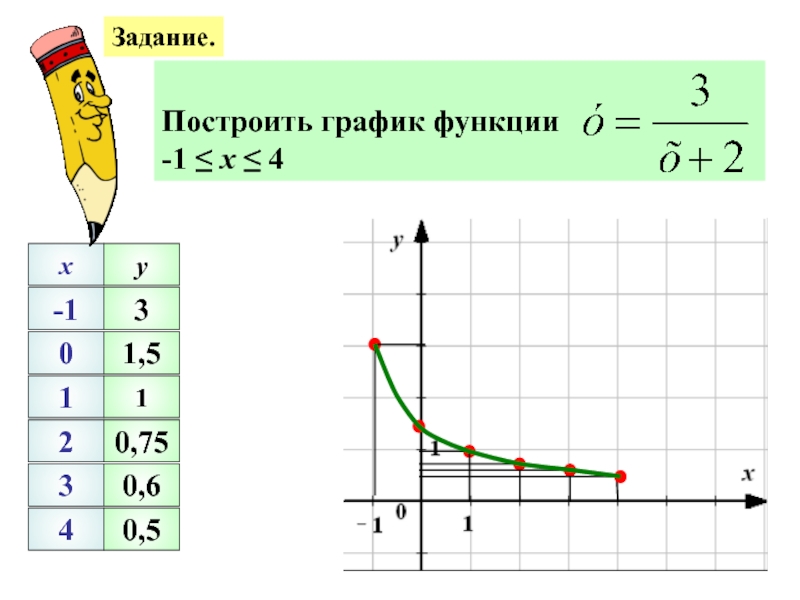
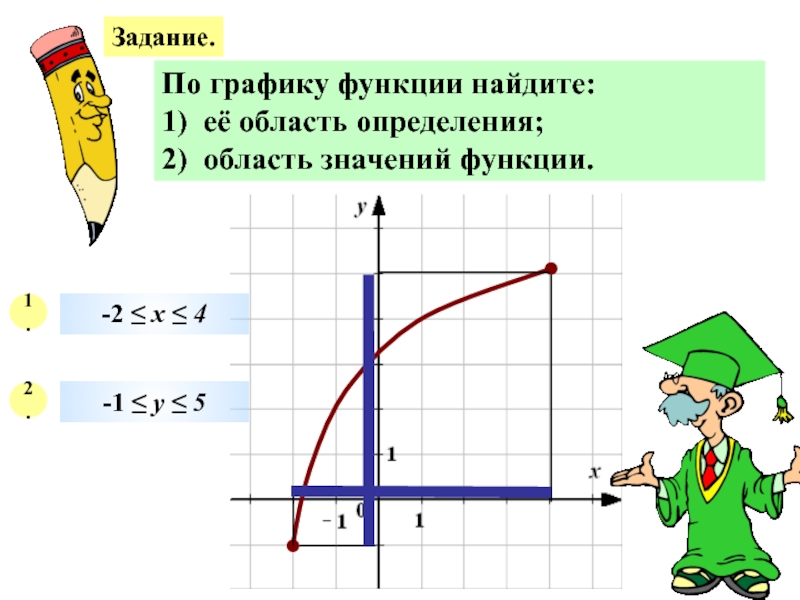
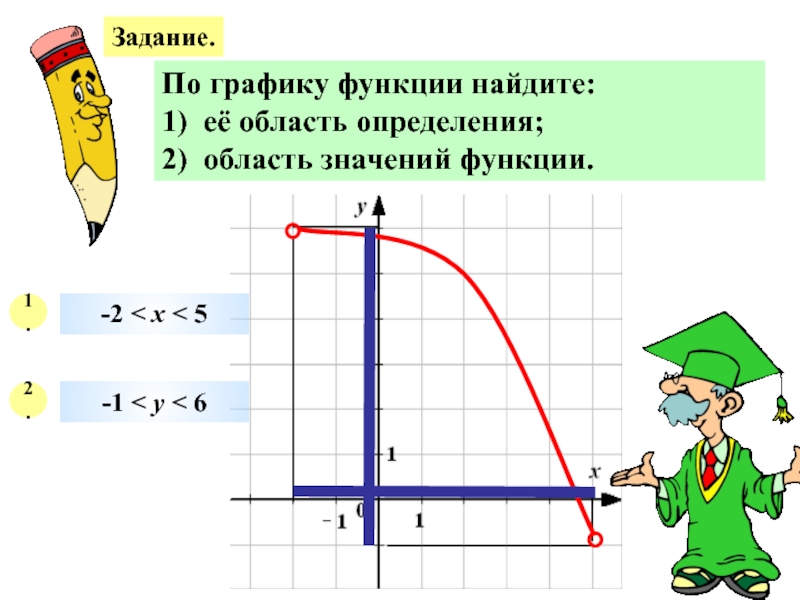
время t ч машина проходит путь
S = 70 ·

Легко вычислить пройденный путь за любое время:

Если t = 1, то

Если t = 1,5, то

Если t = 3, то

S = 70 · 1 = 70

S = 70 · 1,5 = 105

S = 70 · 3 = 210

S = 70 · t

Независимая переменная
АРГУМЕНТ

Зависимая переменная
ФУНКЦИЯ

независимая переменная
Переменная T - зависимая переменная

t
Описание движения машины
В течении 1-го часа машина разгоняется до

От 1ч до 3ч машина движется с постоянной скоростью

От 3ч до 4ч машина тормозит, её скорость уменьшается до 0

От 4ч до 6ч машина стоит, её скорость равна 0

От 6ч до 7ч машина разгоняется до скорости 80 км/ч

От 7ч до 9ч машина движется со скоростью 80 км/ч

t
Из графика можно найти скорость
машины v в любой момент

Если t = 0,5, то…

Если t = 1,5, то…

Если t = 3,5, то…

Если t = 5, то…

Если t = 6,5, то…

Если t = 8, то…

v = 25

v = 50

v = 25

v = 0

v = -40

v = -80

t – выбираем произвольно.
t – независимая переменная.

t
Из графика можно найти скорость
машины v в любой момент

Если t = 0,5, то…

Если t = 1,5, то…

Если t = 3,5, то…

Если t = 5, то…

Если t = 6,5, то…

Если t = 8, то…

v = 25

v = 50

v = 25

v = 0

v = -40

v = -80

Что означает знак «-» в значении скорости?

3
a = 4
S = a2





























S = 4
S = 9
S =

ФУНКЦИЯ

АРГУМЕНТ

значение у
у = х2

АРГУМЕНТ
ФУНКЦИЯ

другой называют
функциональной зависимостью
или функцией.

значение функции

v в зависимости от времени t



Какие значения (по графику) принимает

0 ≤ t ≤ 9

Какие значения (по графику) принимает v ?

-80 ≤ v ≤ 50

Область определения

Область значения

постоянной скоростью
70 км/ч. За время t ч машина проходит

Какие значения может принимать t ?

Какие значения может принимать S ?

t ≥ 0

S ≥ 0

Все значения, которые принимает независимая переменная образуют область определения функции

Значения зависимой переменной образуют
область значений функции

– длина ребра куба, V см3 – его объём.
Задайте формулой

Проверка.(3)

а

а

а

V = а3

Если а = 5, то V = 53 = 125

Если а = 7,1, то V = 357,911

соответствующее
значение функции путём вычислений.
Пример 1.
Найти значение функции y(x) = x3

1.

у(-2) = (-2)3 + (-2) = -8 – 2 = -10

2.

у(5) = 53 + 5 = 125 + 5 = 130

3.

у(а) = а3 + а

4.

у(3а) = (3а)3 + 3а = 27а3 + 3а

найти величину у.
1.
у(3,7) = 1
Т.к. х > 0, то пользуемся

2.

у(0) = 0

Т.к. х = 0, то используем вторую строчку.

3.

у(-2) = -1

Т.к. х < 0, то пользуемся третьей строчкой.

из промежутка 2 ≤ х ≤ 9
2.
В этом случае область

Посмотреть решение

2.

3.

.

-6

-4

-3

-2,5

-1

2

Заполните таблицу.

13

3

-3

-5

-3

13

абсциссы которых равны
значениям аргумента, а ординаты – соответствующим
значениям

Вспомним:

IV

III

II

I

абсциссы которых равны
значениям аргумента, а ординаты – соответствующим
значениям

Вспомним:

A (-4; 6)

B (5; -3)

C (2; 0)

D (0; -5)

-1
0
1
2
3
4
x
y
1
0,75
0,6
0,5
3
1,5

= 3;
2) значение аргумента при котором у = 4

1.

х = 3

у = 2

3

2

2.

у = 4

4

4

х = 4

1.
х –

2.

у ≥ -1

1.
2.


-2 ≤

-1 ≤ у ≤ 5

1.
2.


-2

-1 < у < 6

представляет собой дробь, то её знаменатель
не может равняться нулю, т.е.

и

Итак, область определения данной функции –
Все значения х, кроме чисел -3 и 1.