Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ГИА 2013 Модуль Алгебра №3 9 класс
Содержание
- 1. ГИА 2013 Модуль Алгебра №3 9 класс
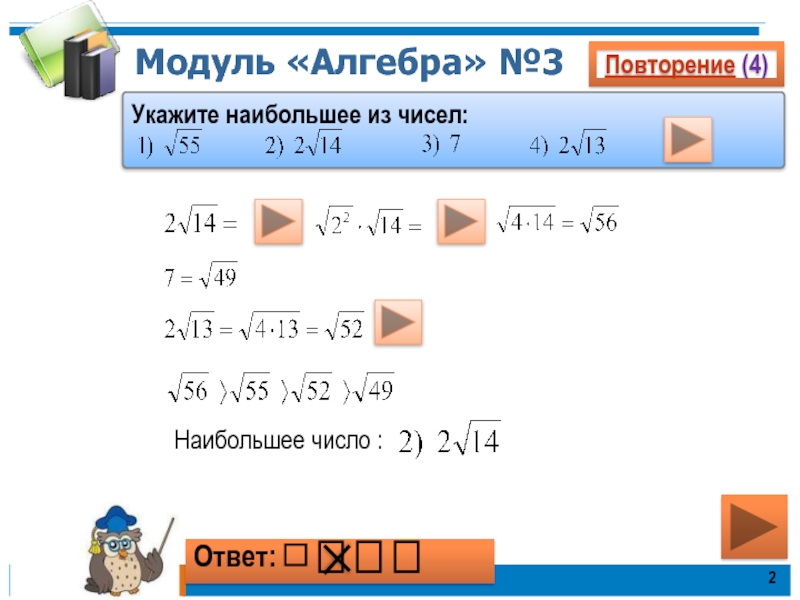
- 2. Модуль «Алгебра» №3Наибольшее число : Повторение (4)Укажите наибольшее из чисел:Ответ: ⎕ ⎕ ⎕ ⎕
- 3. Повторение (подсказка)Чтобы сравнить выражения, содержащие радикал (в
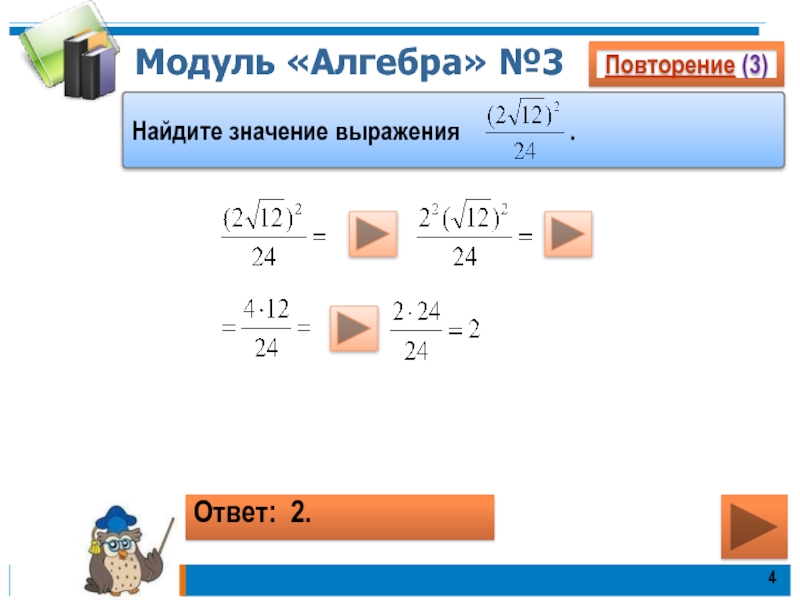
- 4. Модуль «Алгебра» №3Повторение (3)Найдите значение выражения
- 5. Повторение (подсказка)Чтобы возвести в степень произведение, надо
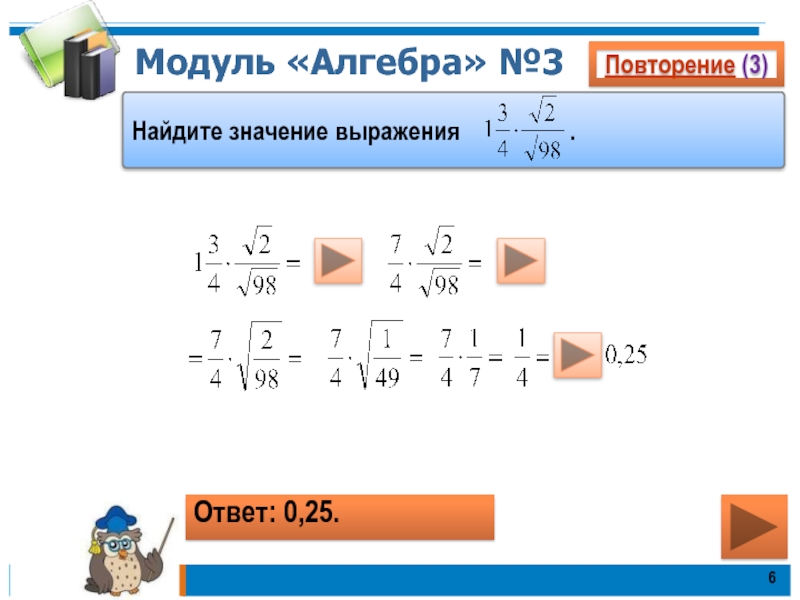
- 6. Модуль «Алгебра» №3Повторение (3)Ответ: 0,25.Найдите значение выражения .
- 7. Повторение (подсказка)Чтобы записать смешанное число в виде
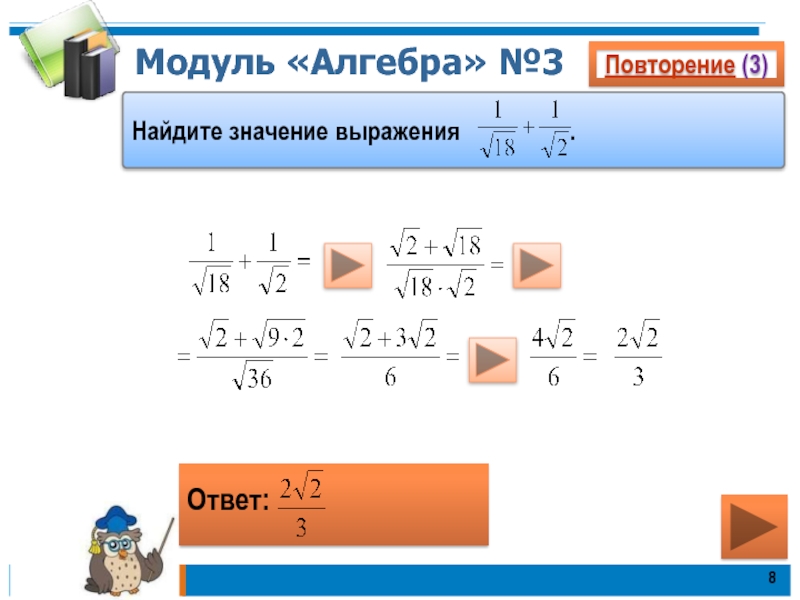
- 8. Модуль «Алгебра» №3Повторение (3)Ответ: Найдите значение выражения .
- 9. Повторение (подсказка)Чтобы сложить дроби с разными знаменателями,
- 10. Модуль «Алгебра» №3Повторение (2)Расположите в порядке убывания:Ответ:
- 11. кликнуть
- 12. Модуль «Алгебра» №3Повторение (2)Сколько целых чисел расположено
- 13. кликнуть
- 14. Модуль «Алгебра» №3Повторение (1)Одно из чисел отмечено
- 15. Повторение (подсказка)Чтобы сравнить данные числа с ближайшими
- 16. Модуль «Алгебра» №3Повторение (1)Одна из точек, отмеченных
- 17. Повторение (подсказка)Чтобы сравнить данное число с координатами, надо эти координаты записать с виде квадратных корней.
- 18. Модуль «Алгебра» №3Повторение (5)Между какими соседними целыми
- 19. Повторение (подсказка)Квадрат суммы двух выражений вычисляется по
- 20. кликнуть
- 21. Использованные ресурсыhttp://www.bigstockphoto.com/r http://education.simcat.ru/schhttp://4149661.ru/katalog/sten Автор шаблона Larisa Vladislavovna
- 22. Скачать презентанцию
Модуль «Алгебра» №3Наибольшее число : Повторение (4)Укажите наибольшее из чисел:Ответ: ⎕ ⎕ ⎕ ⎕
Слайды и текст этой презентации
Слайд 1Модуль «АЛГЕБРА»
№3
Автор презентации:
Гладунец Ирина Владимировна
учитель математики МБОУ гимназии №1
г.Лебедянь Липецкой области
Слайд 2Модуль «Алгебра» №3
Наибольшее число :
Повторение (4)
Укажите наибольшее из чисел:
Ответ:
⎕ ⎕ ⎕ ⎕
Слайд 3Повторение (подсказка)
Чтобы сравнить выражения, содержащие радикал (в частности квадратные корни),
надо внести множители под знак корня и сравнить подкоренные выражения.
Чтобы
внести множитель под знак корня, надо этот множитель возвести в квадрат и записать его под знаком корня.Чтобы перемножить квадратные корни из неотрицательных множителей, надо перемножить эти множители под общим знаком корня.
Чтобы сравнить квадратные корни, надо сравнить подкоренные выражения. Тот корень больше, у которого подкоренное выражение больше.
Слайд 5Повторение (подсказка)
Чтобы возвести в степень произведение, надо каждый множитель возвести
в данную степень.
Возведение числа в квадрат и извлечение квадратного корня
из этого же числа – два взаимно обратные действия, поэтому эти действия друг друга взаимно уничтожают.Чтобы сократить дробь, надо числитель и знаменатель дроби разделить на одно и то же число, не равное нулю.
Слайд 7Повторение (подсказка)
Чтобы записать смешанное число в виде неправильной дроби, надо
целую часть умножить на знаменатель, прибавить числитель и результат записать
в числитель, знаменатель оставить тот же.Если в дроби и числитель и знаменатель содержат квадратные корни, то можно записать дробь под общим знаком корня.
Если в ответе получили обыкновенную дробь, то по возможности надо ее перевести в десятичную. Для этого надо числитель разделить на знаменатель.
Слайд 9Повторение (подсказка)
Чтобы сложить дроби с разными знаменателями, надо дроби привести
к общему знаменателю и сложить числители.
Чтобы вынести множитель из-под знака
корня, надо подкоренное число разложить на такие множители, чтобы из одного из них извлекался корень.Подобными слагаемыми называются те, которые имеют одну и ту же буквенную часть Общий множитель). Квадратный корень из одного и того же числа может играть роль такого же общего множителя
Слайд 10Модуль «Алгебра» №3
Повторение (2)
Расположите в порядке убывания:
Ответ: ⎕ ⎕ ⎕
⎕
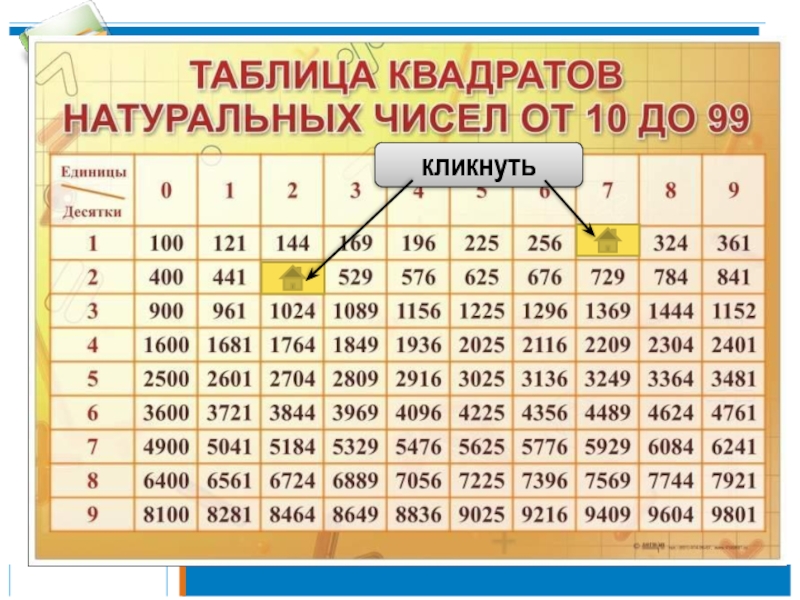
Оценим выражения, содержащие квадратные корни.
Для этого воспользуемся таблицей квадратов.
⇒
⇒
⇒
Слайд 12Модуль «Алгебра» №3
Повторение (2)
Сколько целых чисел расположено между числами
и .
Ответ: 1.
Между данными числами находится только одно целое число 13.
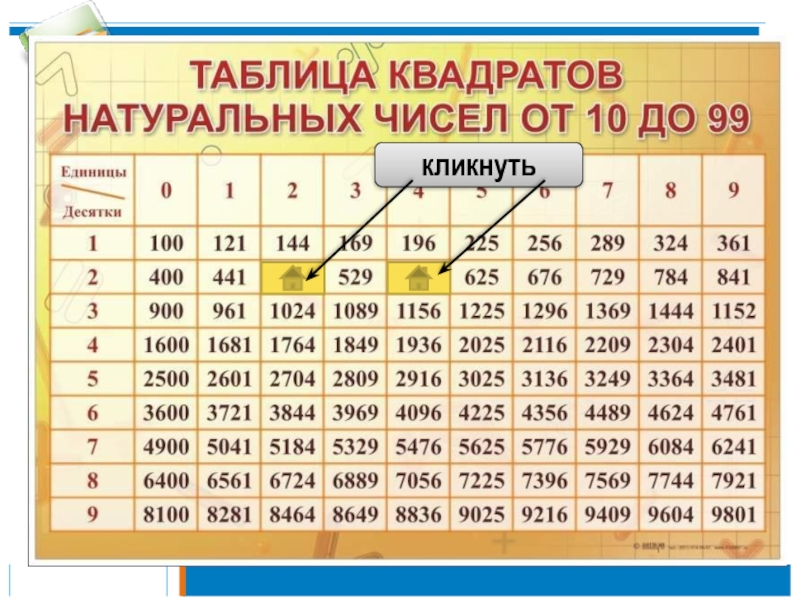
Оценим выражения, содержащие квадратные корни.
Для этого воспользуемся таблицей квадратов.
⇒
Слайд 14Модуль «Алгебра» №3
Повторение (1)
Одно из чисел отмечено на координатной прямой
точкой А. Какое число отмечено точкой А?
Ответ: ⎕ ⎕ ⎕
⎕Между числами 4 и 5 находятся и .
⇒
Но к числу 4 ближе находится число .
Слайд 15Повторение (подсказка)
Чтобы сравнить данные числа с ближайшими с точкой А
координатами, надо эти координаты записать с виде квадратных корней.
Слайд 16Модуль «Алгебра» №3
Повторение (1)
Одна из точек, отмеченных на координатной прямой,
соответствует числу . Какая это точка?
1)А; 2)В; 3)С; 4)D.Ответ: ⎕ ⎕ ⎕ ⎕
Число находится между числами 1 и 2.
⇒
Но число находится ближе к числу 2.
0
4
3
2
1
A
B
C
D
⇒
соответствует точке В.
Слайд 17Повторение (подсказка)
Чтобы сравнить данное число с координатами, надо эти координаты
записать с виде квадратных корней.
Слайд 18Модуль «Алгебра» №3
Повторение (5)
Между какими соседними целыми числами находится выражение
?
Ответ: 18;
19. ⇒
⇒
По таблице квадратов видно, что
⇒
⇒
Слайд 19Повторение (подсказка)
Квадрат суммы двух выражений вычисляется по формуле
.
Чтобы ответить на вопрос задания, надо найти приближенное значение квадратного корня с точностью до целых.
Одно из свойств числовых неравенств говорит, что , если .
Одно из свойств числовых неравенств говорит, что , если
Слайд 21Использованные ресурсы
http://www.bigstockphoto.com/r
http://education.simcat.ru/sch
http://4149661.ru/katalog/sten
Автор шаблона Larisa Vladislavovna Larus http://www.proshkolu.ru/user/vladislava22/
«ГИА-2013. Математика:
типовые экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова,
И. В. Ященко. – М.: Изд. «Национальное образование», 2013.
