Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Влияние модуля на график линейной функции
Содержание
- 1. Влияние модуля на график линейной функции
- 2. АктуализацияРаботать с графиками функций мы начали в
- 3. Цель:Выявить закономерности изменения графика линейной функции при
- 4. Задачи:Вспомнить необходимый теоретический материал и систематизировать его.Опытным
- 5. ГипотезаПредположим, что:1. Существуют такие точки на прямой,
- 6. Методы и средства исследования.Изучение литературы.Проведение эксперимента.Наблюдение и анализ увиденного.
- 7. План исследования.Изучение теории.Построение графика линейной функции, содержащей
- 8. У=2х-3У=|2х-3|хуУ = | 2х – 3 |Построение
- 9. Построение графика функции:У = 2 | х
- 10. Решить уравнение:| 2 х – 3 |
- 11. Решить неравенство:| 2 х – 3 | < 71,5У=|2х – 3|7У=7-25Ответ: -2
- 12. Выводы.Используя результаты данной работы, можно легко и
- 13. Решить уравнение:2 | х | - 3
- 14. Решить неравенство:2 | х | - 3
- 15. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Цель:
Выявить закономерности изменения графика линейной функции при наличии знака модуля.
Разработать
план построения графика линейной функции при наличия знака модуля.
Обосновать рациональность,
наглядность решения некоторых линейных уравнений и неравенств, содержащих знак модуля, графическим способом.Слайд 4Задачи:
Вспомнить необходимый теоретический материал и систематизировать его.
Опытным путём (по точкам)
построить графики линейных функций, содержащих модуль.
Проанализировав полученные результаты, составить план
построения графика линейной функции, содержащей знак модуля.На конкретных примерах показать простоту и наглядность графического способа решения уравнений и неравенств с модулем.
Слайд 5Гипотеза
Предположим, что:
1. Существуют такие точки на прямой, положение которых на
координатной плоскости
не меняется при появлении модуля;
меняется при появлении модуля;
2. Для
одной и той же прямой имеет большое значение, где поставлен знак модуля.Слайд 6Методы и средства исследования.
Изучение литературы.
Проведение эксперимента.
Наблюдение и анализ увиденного.
Слайд 7План исследования.
Изучение теории.
Построение графика линейной функции, содержащей знак модуля, опытным
путём.
Выявление закономерностей поведения графика.
Составление плана построения графика линейной функции, содержащей
знак модуля.Практическое применение полученных результатов при решении уравнений и неравенств.
Слайд 8У=2х-3
У=|2х-3|
х
у
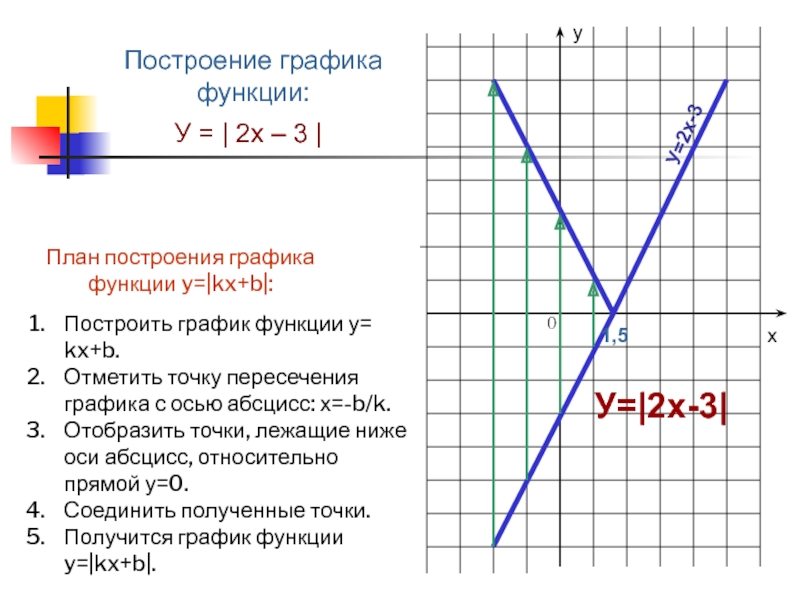
У = | 2х – 3 |
Построение графика функции:
1,5
Построить график
функции у= kx+b.
Отметить точку пересечения графика с осью абсцисс: х=-b/k.
Отобразить
точки, лежащие ниже оси абсцисс, относительно прямой у=0.Соединить полученные точки.
Получится график функции y=|kx+b|.
0
План построения графика функции y=|kx+b|:
Слайд 9Построение графика функции:
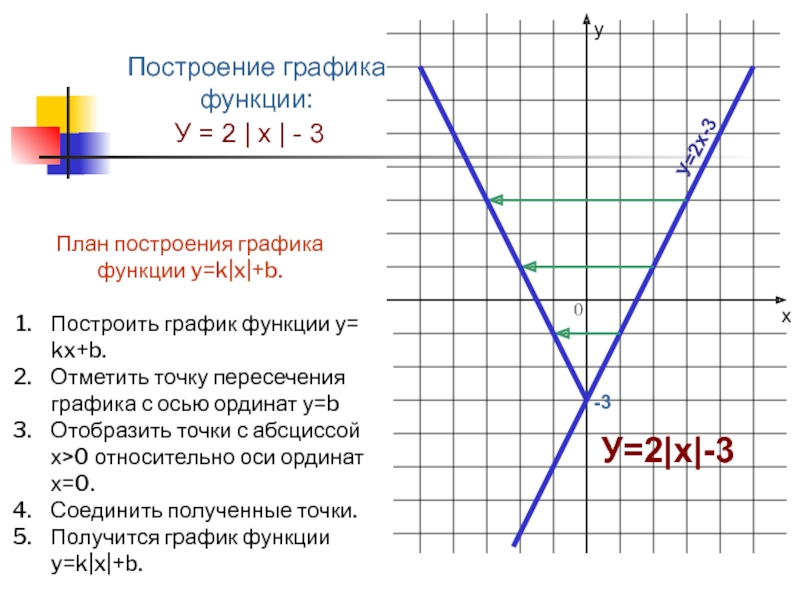
У = 2 | х | - 3
У=2х-3
У=2|х|-3
-3
х
у
Построить
график функции у= kx+b.
Отметить точку пересечения графика с осью ординат
у=bОтобразить точки с абсциссой х>0 относительно оси ординат х=0.
Соединить полученные точки.
Получится график функции y=k|x|+b.
0
План построения графика функции y=k|x|+b.
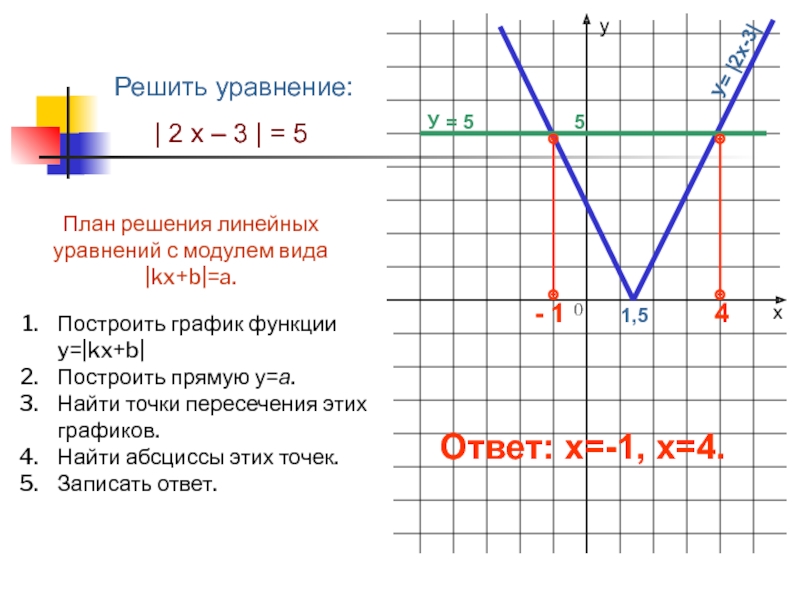
Слайд 10Решить уравнение:
| 2 х – 3 | = 5
У =
5
У= |2х-3|
- 1
4
у
х
1,5
5
Ответ: х=-1, х=4.
0
Построить график функции y=|kx+b|
Построить прямую у=а.
Найти
точки пересечения этих графиков.Найти абсциссы этих точек.
Записать ответ.
План решения линейных уравнений с модулем вида |kx+b|=a.
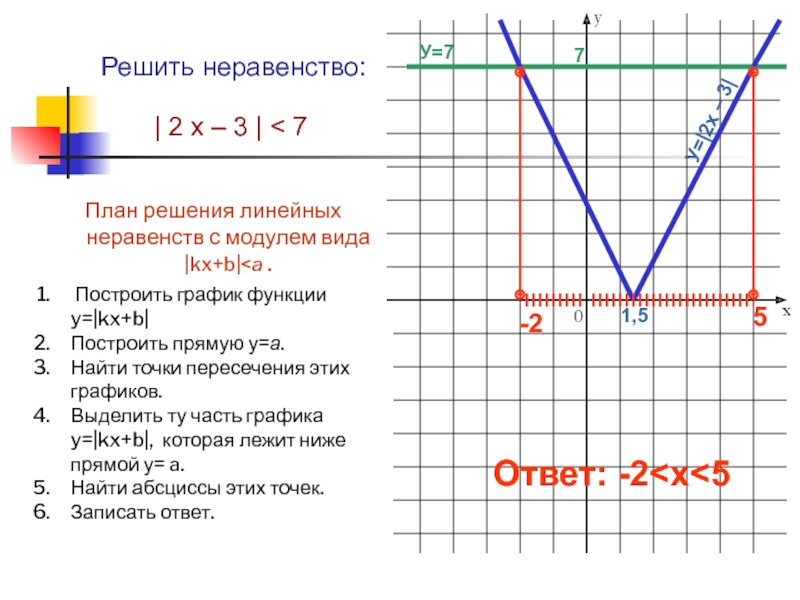
Слайд 11Решить неравенство:
| 2 х – 3 | < 7
1,5
У=|2х –
3|
7
У=7
-2
5
Ответ: -2
Построить график функции y=|kx+b|
Построить прямую у=а.
Найти точки пересечения этих графиков.
Выделить ту часть графика y=|kx+b|, которая лежит ниже прямой у= a.
Найти абсциссы этих точек.
Записать ответ.
Слайд 12Выводы.
Используя результаты данной работы, можно легко и наглядно решать линейные
уравнения и неравенства с модулем графическим методом.
Данная работа является
только начальным этапов в освоении графического метода решения уравнений и неравенств. По мере изучения различных функций область применения этого метода можно значительно расширить.
Например, на следующий год мы планируем продолжить начатую исследовательскую работу, рассмотрев квадратичную функцию, содержащую знак модуля.
Работа в этом направлении поможет при подготовке к экзаменам.
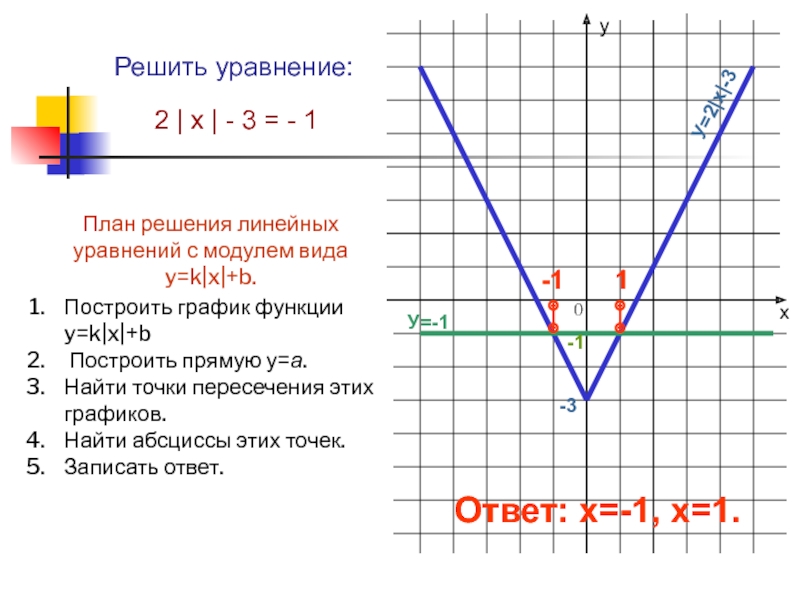
Слайд 13Решить уравнение:
2 | х | - 3 = - 1
-3
-1
1
х
у
-1
У=2|х|-3
У=-1
Ответ:
х=-1, х=1.
0
План решения линейных уравнений с модулем вида y=k|x|+b.
Построить
график функции y=k|x|+bПостроить прямую у=а.
Найти точки пересечения этих графиков.
Найти абсциссы этих точек.
Записать ответ.
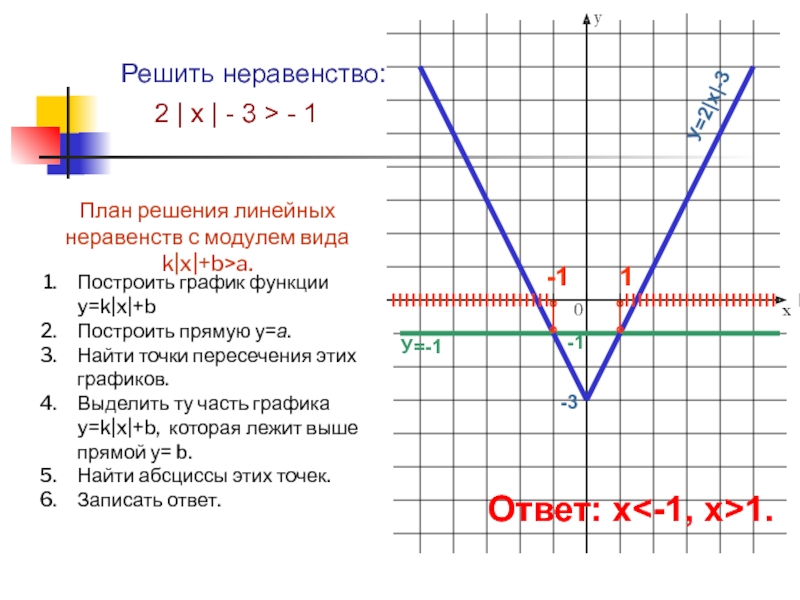
Слайд 14Решить неравенство:
2 | х | - 3 > - 1
У=2|х|-3
У=-1
-1
-3
-1
1
х
у
0
Ответ:
х1.
План решения линейных неравенств с модулем вида k|x|+b>a.
Построить график
функции y=k|x|+bПостроить прямую у=а.
Найти точки пересечения этих графиков.
Выделить ту часть графика y=k|x|+b, которая лежит выше прямой у= b.
Найти абсциссы этих точек.
Записать ответ.