Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ГИА 2013 Модуль Алгебра №7 9 класс
Содержание
- 1. ГИА 2013 Модуль Алгебра №7 9 класс
- 2. Модуль «Алгебра» №71 способ:(a+b)²(a-b)²=(a²+2ab+b²)(a²-2ab+b²)==a⁴-2a³b+a²b²+2a³b-4a²b²+2ab³+a²b²-2ab³+b⁴== a⁴-2a²b²+b⁴Повторение (5)Ответ: 1
- 3. Повторение (подсказка)Квадрат суммы (разности) двух выражений равен
- 4. Модуль «Алгебра» №7Повторение (2)Ответ: 2,05 Сократите дробь
- 5. Повторение (подсказка)Чтобы сократить дробь, надо и числитель,
- 6. Модуль «Алгебра» №7Повторение (4)Ответ: Сократите дробь
- 7. Повторение (подсказка)Разность квадратов равна произведению разности этих
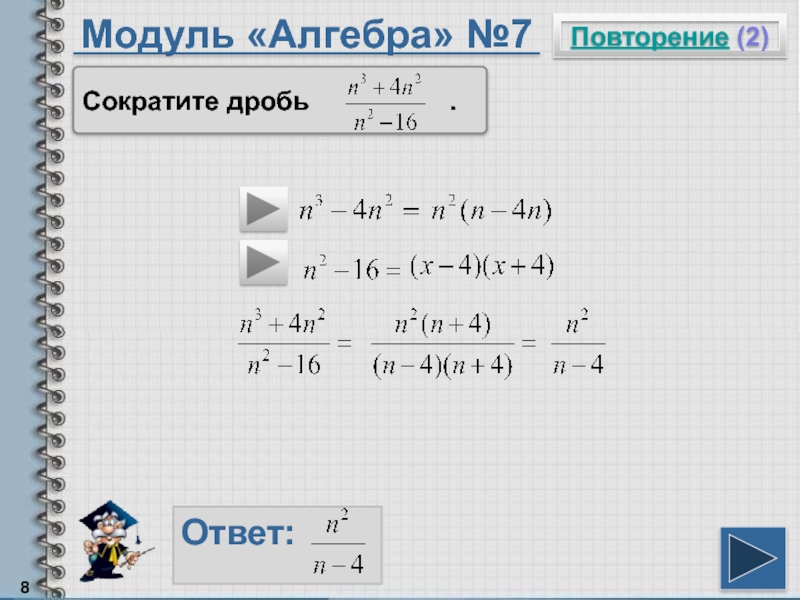
- 8. Модуль «Алгебра» №7Повторение (2)Ответ: Сократите дробь .
- 9. Повторение (подсказка)Если у слагаемых есть общий множитель,
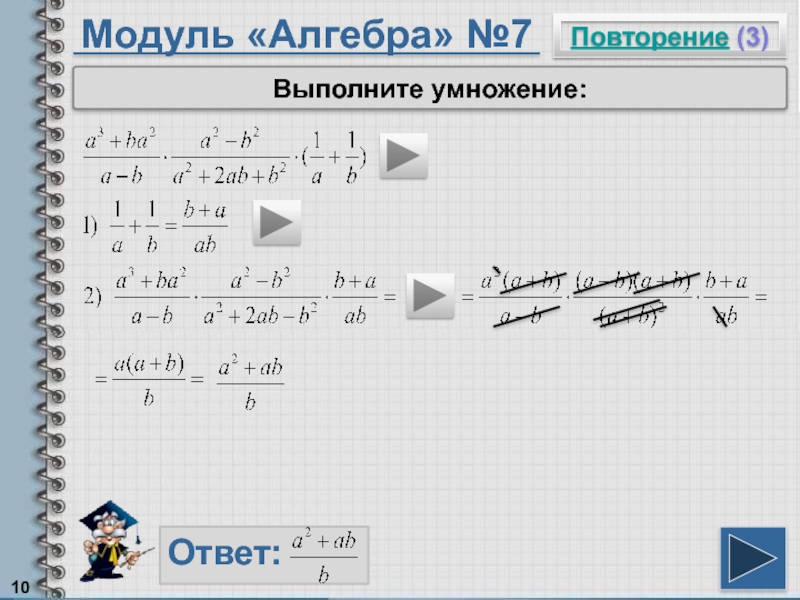
- 10. Модуль «Алгебра» №7Повторение (3)Ответ: Выполните умножение:
- 11. Повторение (подсказка)Чтобы сложить дроби с разными знаменателями,
- 12. Модуль «Алгебра» №7Повторение (1)Ответ: Выполните деление:
- 13. Повторение (подсказка)Чтобы разделить дробь на дробь, надо
- 14. Модуль «Алгебра» №7Повторение (2)Ответ: Упростите выражение:
- 15. Повторение (подсказка)Чтобы сложить с дробью натуральное число,
- 16. Модуль «Алгебра» №7Повторение (2)Ответ: Выполните умножение:
- 17. Повторение (подсказка)Сумму кубов двух выражений можно разложить по формулеДробь, знаменатель которой равен единице, является целым выражением.
- 18. Модуль «Алгебра» №7Повторение (4)Ответ: Выполните умножение:
- 19. Повторение (подсказка)Чтобы сложить дробь с одночленом, надо
- 20. Модуль «Алгебра» №7Повторение (5)Ответ: Найдите значение выражения при n= :
- 21. Повторение (подсказка)Чтобы проще выполнить задание, надо выражение
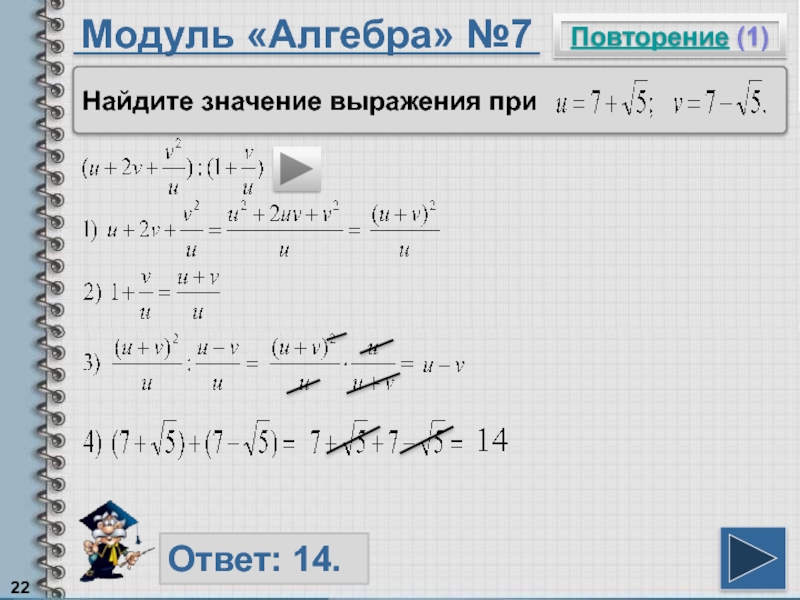
- 22. Модуль «Алгебра» №7Повторение (1)Ответ: 14. Найдите значение выражения при
- 23. Повторение (подсказка)Сначала надо выполнить действия с рациональными дробями.
- 24. Модуль «Алгебра» №7Повторение (3)Ответ: 84. Найдите значение выражения при
- 25. Повторение (подсказка)Числитель дроби можно записать в виде
- 26. Использованные ресурсыhttp://www.grafamania.net/uploads/posts/2008-08/1219611582_7.jpg Автор шаблона Larisa Vladislavovna Larus
- 27. Скачать презентанцию
Модуль «Алгебра» №71 способ:(a+b)²(a-b)²=(a²+2ab+b²)(a²-2ab+b²)==a⁴-2a³b+a²b²+2a³b-4a²b²+2ab³+a²b²-2ab³+b⁴== a⁴-2a²b²+b⁴Повторение (5)Ответ: 1 Преобразуйте в многочлен выражение (a+b)²(a-b)². Найдите значение многочлена при 2 способ:(a+b)²(a-b)² = (a+b)(a-b)∙(a+b)(a-b) = (a²-b²)² = a⁴-2a²b²+b⁴
Слайды и текст этой презентации
Слайд 1ГИА 2013.
Модуль «АЛГЕБРА»
№7
Автор презентации:
Гладунец Ирина Владимировна
учитель математики МБОУ гимназии
№1 г.Лебедянь Липецкой области
Слайд 2Модуль «Алгебра» №7
1 способ:
(a+b)²(a-b)²=(a²+2ab+b²)(a²-2ab+b²)=
=a⁴-2a³b+a²b²+2a³b-4a²b²+2ab³+a²b²-2ab³+b⁴=
= a⁴-2a²b²+b⁴
Повторение (5)
Ответ: 1
Преобразуйте в многочлен
выражение (a+b)²(a-b)². Найдите значение многочлена при
2 способ:
(a+b)²(a-b)² = (a+b)(a-b)∙(a+b)(a-b)
= (a²-b²)² = a⁴-2a²b²+b⁴
Слайд 3Повторение (подсказка)
Квадрат суммы (разности) двух выражений равен квадрату первого выражения
плюс (минус) удвоенное произведение первого и второго выражений и плюс
квадрат второго выражения.Чтобы умножить многочлен на многочлен, надо умножить каждый член одного многочлена на каждый член другого многочлена.
Если у слагаемых одинаковая буквенная часть, то они подобны. При сложении таких слагаемых складывают коэффициенты и умножают на общую буквенную часть.
Произведение разности двух выражений на их сумму равно разности квадратов этих выражений.
Если квадратный корень возвести в квадрат, то получим подкоренное выражение.
Слайд 4Модуль «Алгебра» №7
Повторение (2)
Ответ: 2,05
Сократите дробь
.
Найдите значение выражения при а = 3,05
и b=
Слайд 5Повторение (подсказка)
Чтобы сократить дробь, надо и числитель, и знаменатель разложить
на множители.
Чтобы перевести обыкновенную дробь в десятичную, надо числитель разделить
на знаменатель.
Слайд 7Повторение (подсказка)
Разность квадратов равна произведению разности этих выражений на из
сумму.
Квадратный трехчлен можно разложить на множители по формуле
Корни квадратного
трехчлена можно найти по формулам:Чтобы сократить дробь, надо и числитель и знаменатель разделить на одно и тоже выражение, не равное нулю.
Слайд 9Повторение (подсказка)
Если у слагаемых есть общий множитель, то при разложении
многочлена на множители этот множитель можно вынести за скобку.
Разность квадратов
можно разложить по формуле:
Слайд 11Повторение (подсказка)
Чтобы сложить дроби с разными знаменателями, надо привести дроби
к общему знаменателю и сложить числители.
Чтобы умножить дроби, надо отдельно
умножить числители и знаменатели.В процессе умножения дробей можно сокращать. Для этого надо числители и знаменатели дробей разложить на множители
Трехчлен a²+2ab+b² можно «свернуть» по формуле
Слайд 13Повторение (подсказка)
Чтобы разделить дробь на дробь, надо первую дробь умножить
на обратную второй дроби.
Сумма противоположных слагаемых равна нулю.
Слайд 15Повторение (подсказка)
Чтобы сложить с дробью натуральное число, надо это число
представить в виде дроби со знаменателем 1 и сложить по
правилу дробей.Произведение двух одинаковых множителей можно записать в виде квадрата этого множителя.
Слайд 17Повторение (подсказка)
Сумму кубов двух выражений можно разложить по формуле
Дробь, знаменатель
которой равен единице, является целым выражением.
Слайд 19Повторение (подсказка)
Чтобы сложить дробь с одночленом, надо одночлен заменить дробью
со знаменателем 1 и выполнить сложение дробей.
Чтобы разложить многочлен на
множители (в случае, если формулы сокращенного умножения на подходят), можно применить способ группировки.Далее надо каждую скобку разложить на множители своим способом.
Далее общий множитель в виде многочлена вынести за скобку.
Слайд 21Повторение (подсказка)
Чтобы проще выполнить задание, надо выражение с переменными упростить.
Чтобы
упростить запись дроби, ее надо сократить, а для этого надо
числитель и знаменатель разложить на множители.Чтобы вынести общий множитель за скобки, надо разделить каждое слагаемое на этот множитель.
Чтобы записать натуральное число в виде квадрата, надо его заключить под знак квадратного корня.
Чтобы «избавиться» от иррациональности в знаменателе, надо числитель и знаменатель умножить на иррациональный множитель.
Слайд 25Повторение (подсказка)
Числитель дроби можно записать в виде разности кубов и
разложить на множители по формуле
Если квадратный корень возвести в квадрат,
то получится подкоренное число.Произведение квадратных корней из неотрицательных множителей равно квадратному корню из произведения этих множителей..
Слайд 26Использованные ресурсы
http://www.grafamania.net/uploads/posts/2008-08/1219611582_7.jpg
Автор шаблона Larisa Vladislavovna Larus http://www.proshkolu.ru/user/vladislava22/
«ГИА-2013. Математика: типовые
экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова, И.
В. Ященко. – М.: Изд. «Национальное образование», 2013.
