Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производная. Решение прикладных задач 10 класс
Содержание
- 1. Производная. Решение прикладных задач 10 класс
- 2. Фрагмент рассказа Л.Н. Толстого «Много
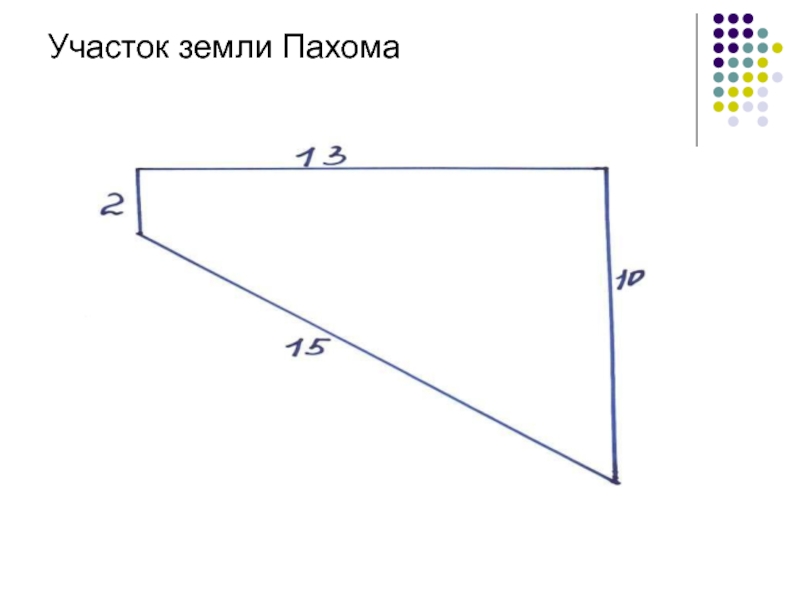
- 3. Участок земли Пахома
- 4. Слайд 4
- 5. Цели урока: углубление понимания сущности производной путем применения её для получения новых знаний;установление межпредметных связей
- 6. Девиз урокаВ математике следует помнить не формулы, а процессы мышленияВ.П. Ермаков
- 7. Алгоритм нахождения наибольшего и наименьшего значения функции.Какие точки называются критическими?Этапы работы с моделью.
- 8. № 953 аПериметр прямоугольника равен 56 см.
- 9. I этап. Составление математической модели.Оптимизируемая величина (О.В.)
- 10. II этап. Работа с составленной модельюНа этом
- 11. Заданному интервалу точка принадлежит. Свое наибольшее значение
- 12. III этап. Ответ на вопрос задачиМы
- 13. А теперь вернемся к задаче, с которой
- 14. Для конструкторского бюро строится комната в форме
- 15. Слайд 15
- 16. I этап. Моделирование.S (ABCD) = ab =
- 17. Общая стоимость всех стенР1= 300а + 400b
- 18. II этап. Работа с математической моделью.
- 19. III этап. Ответ на вопрос задачиШирина
- 20. Домашнее задание952а, 953б, 954а
- 21. Скачать презентанцию
Фрагмент рассказа Л.Н. Толстого «Много ли человеку земли нужно» о крестьянине Пахоме, покупавшему землю у башкир
Слайды и текст этой презентации
Слайд 2Фрагмент рассказа Л.Н. Толстого «Много ли человеку земли нужно» о
крестьянине Пахоме, покупавшему землю у башкир
Слайд 5Цели урока:
углубление понимания сущности производной путем применения её для
получения новых знаний;
установление межпредметных связей
Слайд 7
Алгоритм нахождения наибольшего и наименьшего значения функции.
Какие точки называются критическими?
Этапы
работы с моделью.
Слайд 8№ 953 а
Периметр прямоугольника равен 56 см. Какую длину должны
иметь стороны прямоугольника, чтобы площадь была наибольшей?
Слайд 9I этап. Составление математической модели.
Оптимизируемая величина (О.В.) – площадь, S.
Площадь
зависит от длины и ширины. Объявим независимой переменной (Н.П.) –
длину прямоугольника и обозначим её за х, (28-х) – ширина прямоугольника, тогда0 < x < 28 - реальные границы изменений независимой переменной.
Записываем функцию: S(x) = x(28-x)
Математическая модель составлена.
Слайд 10II этап. Работа с составленной моделью
На этом этапе для функции
S(x) хЄ(0;28) надо найти Sнаиб
Воспользуемся алгоритмом нахождения наибольшего и наименьшего
значения:
Слайд 11Заданному интервалу точка принадлежит.
Свое наибольшее значение функция
S(x) =
x(28-x) достигает при х=14 и
Sнаиб = 196
Слайд 12III этап.
Ответ на вопрос задачи
Мы выяснили, что длина участка,
имеющего наибольшую площадь
равна 14, ширина равна 14.
Слайд 13А теперь вернемся к задаче, с которой мы начали урок.
Значит какую фигуру Пахом должен был обойти?
Р = 40км
, а = 10км, Значит
Sнаиб = 100кв.км.
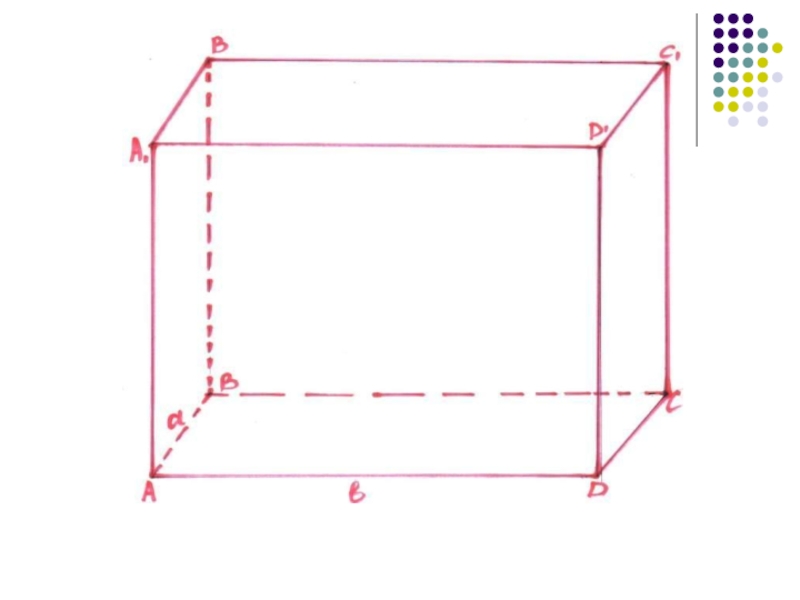
Слайд 14Для конструкторского бюро строится комната в форме прямоугольного параллелепипеда, одна
из стен которой должна быть сделана из стекла, а остальные
из обычного материала. Высота комнаты должна быть 4м., а площадь 80 кв.м. Известно, что 1 кв.м. стеклянной стены стоит 75 рублей, а из обычного материала 50 рублей. Какими должны быть размеры комнаты, чтобы общая стоимость всех стен была наименьшей?
Слайд 16I этап. Моделирование.
S (ABCD) = ab = 80
S(A.B.C.D.) = ah
= 4a
Найдем стоимость стены AA.BB.:
P(AA.BB.) = 75*4a = 300a
S(AA.DD.)
= bh = 4b, тогда Р(AA.DD.) = 200bS(BB.CC.) = bh = 4b, тогда Р(BB.CC.) = 200b
S(CC.DD.) = ah = 4a, тогда Р(CC.DD.) = 50*4а = 200а
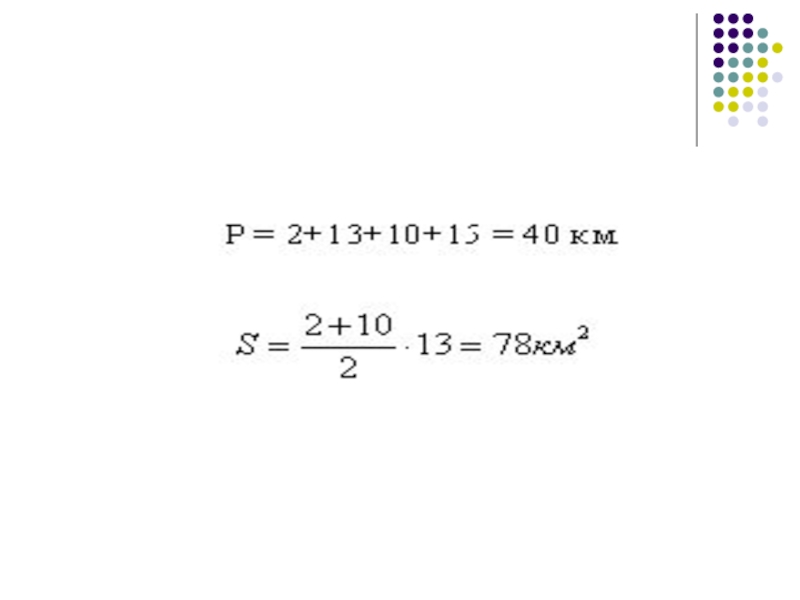
Слайд 17Общая стоимость всех стен
Р1= 300а + 400b + 200а =
500а + 400b, aЄ(0;80/b]
Математическая задача:
исследовать функцию на наименьшее значение
на заданном промежутке.![Общая стоимость всех стенР1= 300а + 400b + 200а = 500а + 400b, aЄ(0;80/b]Математическая задача: исследовать функцию](/img/thumbs/41aa3b14d2603f68ab719a01a8a16bb7-800x.jpg "Производная. Решение прикладных задач 10 класс Общая стоимость всех стенР1= 300а + 400b + 200а = 500а")
Слайд 19III этап.
Ответ на вопрос задачи
Ширина стеклянной стены должна быть
равна 8м, а обычной 10м.
При таких размерах общая стоимость
всех стен окажется наименьшей и равной 8000 рублей
