Разделы презентаций

Системы дифференциальных уравнений

Содержание

Системы дифференциальных уравненийНормальные системы Д.У.Система уравнений видас неизвестными функцияминазывается нормальной системой дифференциальных уравнений.

Слайды и текст этой презентации

Слайд 1Системы дифференциальных уравнений
Общие понятия

Системы дифференциальных уравненийОбщие понятия

Слайд 2Системы дифференциальных уравнений
Нормальные системы Д.У.
Система уравнений вида






с неизвестными функциями

называется нормальной

системой
дифференциальных уравнений.

Системы дифференциальных уравненийНормальные системы Д.У.Система уравнений видас неизвестными функцияминазывается нормальной системой дифференциальных уравнений.

Слайд 3Системы дифференциальных уравнений
Решением системы Д.У.
называется вектор-функция

определенная в

,
имеющая там производную первого порядка и такая, что при

подстановке ее и
ее производных в систему каждое уравнение превращается в тождество.

Производной вектор- функции

называется вектор-функция


Системы дифференциальных уравненийРешением системы Д.У.называется вектор-функцияопределенная в ,имеющая там производную первого порядка и

Слайд 4Системы дифференциальных уравнений
Задача Коши для системы Д.У.:
найти решение системы

такое

, что в некоторой точке
оно удовлетворяет начальному условию

Системы дифференциальных уравненийЗадача Коши для системы Д.У.:найти решение системы такое , что в некоторой точке оно удовлетворяет

Слайд 5Системы дифференциальных уравнений
Векторная запись системы Д.У.
Обозначим:




Получим векторное уравнение


Решение векторного уравнения

– это вектор-функция ,
удовлетворяющая

векторному уравнению:
Системы дифференциальных уравненийВекторная запись системы Д.У.Обозначим:Получим векторное уравнениеРешение векторного уравнения – это вектор-функция

Слайд 6Системы дифференциальных уравнений
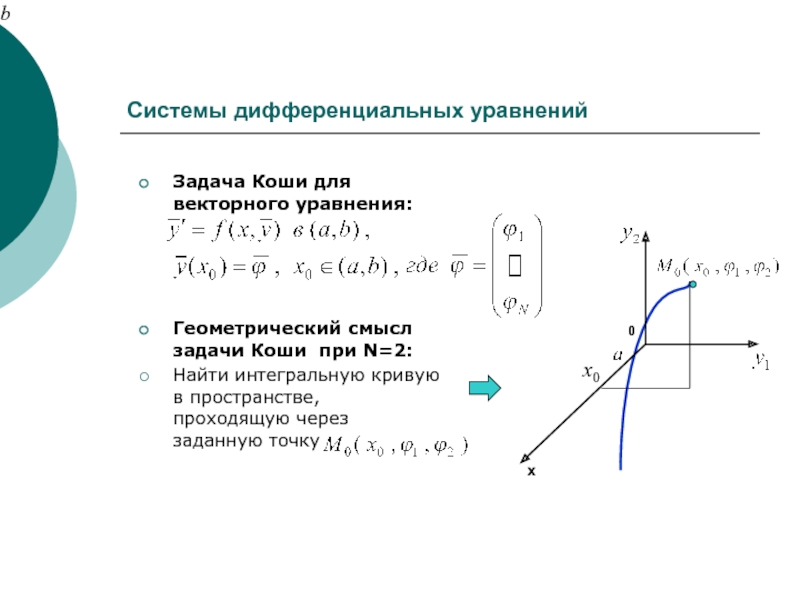
Задача Коши для векторного уравнения:




Геометрический смысл задачи Коши

при N=2:
Найти интегральную кривую в пространстве, проходящую через заданную точку

.



b

Системы дифференциальных уравненийЗадача Коши для векторного уравнения:Геометрический смысл задачи Коши при N=2:Найти интегральную кривую в пространстве, проходящую

Слайд 7Системы дифференциальных уравнений
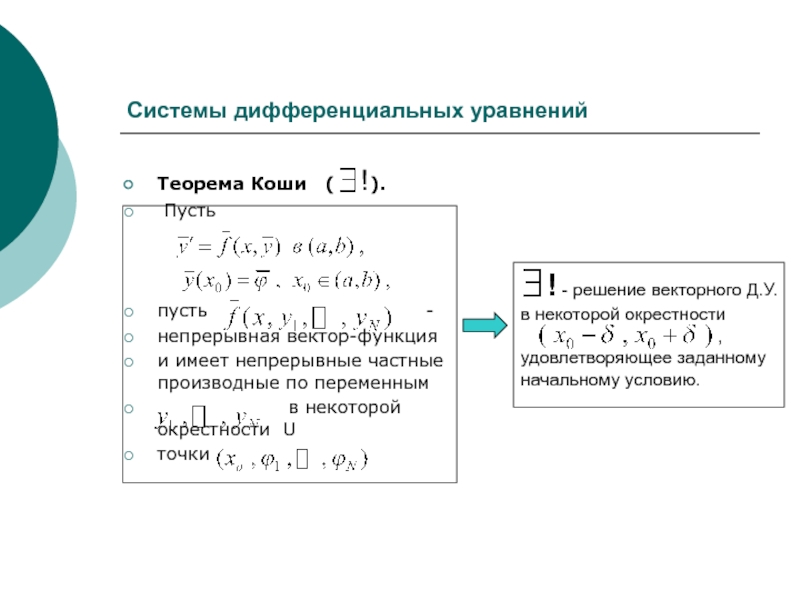
Теорема Коши ( !).
Пусть



пусть

-
непрерывная вектор-функция
и имеет непрерывные частные производные по переменным
в некоторой окрестности U
точки




! - решение векторного Д.У.
в некоторой окрестности
,
удовлетворяющее заданному
начальному условию.


Системы дифференциальных уравненийТеорема Коши ( !). Пустьпусть

Похожие презентации

Свойство периодичности Свойство периодичности 438
Арифметика десятичных дробей Арифметика десятичных дробей 496
Комбинаторные задачи Комбинаторные задачи 473
Путешествие к замку Камелота. Степень и ее свойства. Путешествие к замку Камелота. Степень и ее свойства. 366
Уравнения и неравенства Уравнения и неравенства 1216
Решение уравнений высших степеней 9 класс Решение уравнений высших степеней 9 класс 370
Системы линейных уравнений с двумя переменными Системы линейных уравнений с двумя переменными 640
Квадратный трехчлен и его приложения Квадратный трехчлен и его приложения 478
Интелектуальная игра Мы пока не Архимеды 6-7 класс Интелектуальная игра Мы пока не Архимеды 6-7 класс 391
Среднее арифметическое, размах и мода 7 класс Среднее арифметическое, размах и мода 7 класс 463
Экзаменационная работа по алгебре ГИА – 2010 Экзаменационная работа по алгебре ГИА – 2010 549
Сложение и вычитание смешанных чисел 5 класс Сложение и вычитание смешанных чисел 5 класс 490
Арифметическая прогрессия. Формула n –го члена арифметической прогрессии Арифметическая прогрессия. Формула n –го члена арифметической прогрессии 400
Решение систем уравнений с двумя переменными 9 класс Решение систем уравнений с двумя переменными 9 класс 392
Геометрическая вероятность Геометрическая вероятность 688
Квадратичная функция Квадратичная функция 562
Функция y = x^2 Функция y = x^2 612
Неравенства с двумя переменными и их системы Неравенства с двумя переменными и их системы 495
Свойства арифметического корня П-ОЙ степени Свойства арифметического корня П-ОЙ степени 470
Решение систем неравенств Решение систем неравенств 491

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика