Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы счисления
Содержание
- 1. Системы счисления
- 2. ВведениеСовременный человек в повседневной жизни постоянно сталкивается
- 3. Система счисления – это определённый способ представления
- 4. Древние системы счисления:Единичная системаДревнегреческая нумерацияСлавянская нумерацияРимская нумерация
- 5. Позиционные и непозиционные системы счисления
- 6. Запись числа в позиционной системе счисления Любое
- 7. Примеры позиционных систем счисления:
- 8. История двоичной системы счисленияДвоичная система счисления была
- 9. Двоичная система счисленияДвоичная система счисления (бинарная
- 10. Сложение, вычитание, умножение и деление в двоичной системе счисления
- 11. Двоичное кодирование в компьютереВ конце ХХ века,
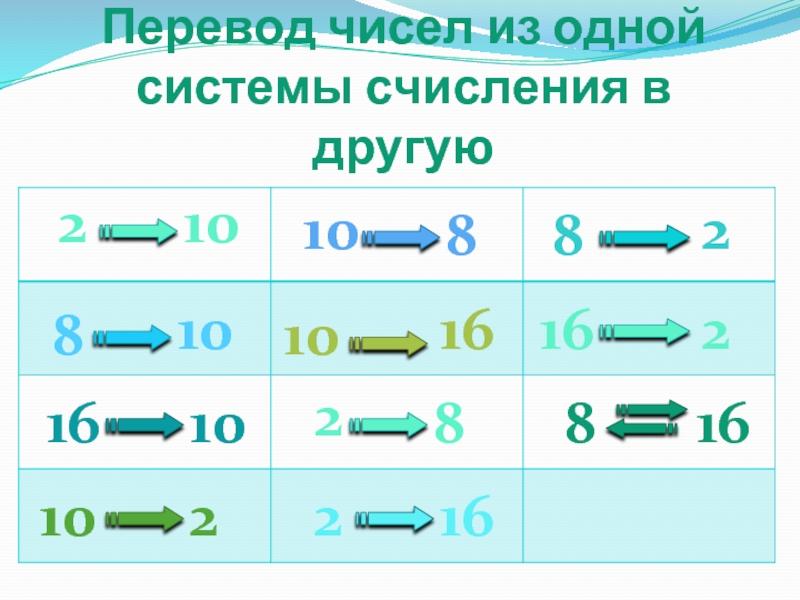
- 12. Перевод чисел из одной системы счисления в другую816
- 13. ЗаключениеВысшим достижением древней арифметики является открытие позиционного
- 14. Слайд 14
- 15. Перевод двоичного числа в десятичноеДля перевода двоичного
- 16. Перевод восьмеричного числа в десятичноеДля перевода восьмеричного
- 17. Перевод шестнадцатеричного числа в десятичноеДля перевода шестнадцатеричного
- 18. Перевод десятичного числа в двоичную системуДля перевода
- 19. Перевод десятичного числа в восьмеричную системуДля перевода
- 20. Перевод десятичного числа в шестнадцатеричную системуДля перевода
- 21. Перевод чисел из двоичной системы в восьмеричнуюЧтобы
- 22. Перевод из двоичной системы в шестнадцатеричнуюЧтобы перевести
- 23. Перевод восьмеричного числа в двоичноеДля перевода восьмеричного
- 24. Перевод шестнадцатеричного числа в двоичноеДля перевода шестнадцатеричного
- 25. Перевод из восьмеричной системы счисления в шестнадцатеричную
- 26. Единичная системаВ древние времена, когда появилась потребность
- 27. Древнегреческая нумерацияАттическая нумерацияИонийская системаВ третьем веке до
- 28. Славянская нумерацияВ России славянская нумерация сохранилась до
- 29. Римская нумерацияДревние римляне пользовались нумерацией, которая сохраняется
- 30. Ионийская системаОбозначение чисел в ионийской системе нумерации
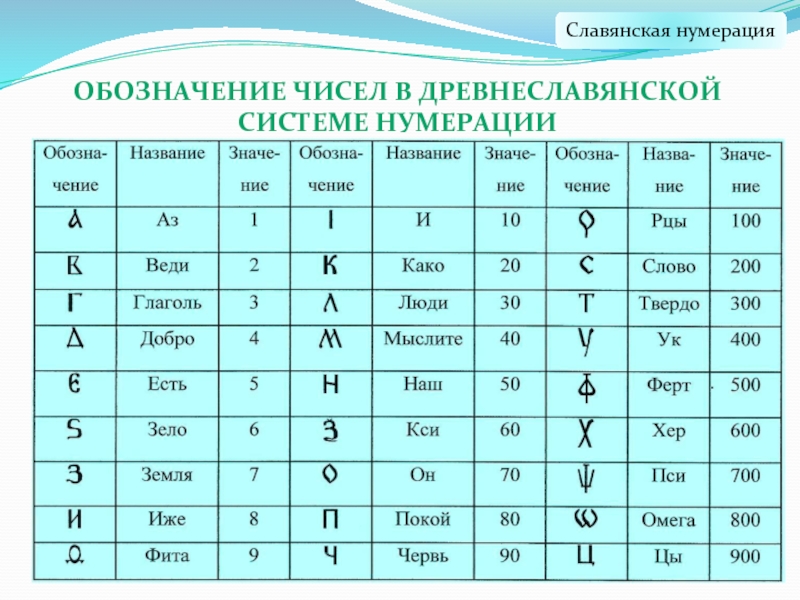
- 31. Обозначение чисел в древнеславянской системе нумерацииСлавянская нумерация
- 32. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Система счисления – это определённый способ представления чисел и соответствующие
ему правила действия над ними.
Цель создания системы счисления- выработка наиболее
удобного способа записи количественной информации.История систем счисления
Системы счисления
Позиционные
Непозиционные
Слайд 4Древние системы счисления:
Единичная система
Древнегреческая нумерация
Славянская нумерация
Римская нумерация
Слайд 6Запись числа в позиционной системе счисления
Любое целое число в
позиционной системе можно записать в форме многочлена:
Хs=An · Sn-1
+ An-1 · Sn-2 + An-2 · Sn-3 +...+ A2 · S1 + A1 · S0где S - основание системы счисления, А – цифры числа, записанного в данной системе счисления, n - количество разрядов числа.
Так, например число 629310запишется в форме многочлена следующим образом:
629310=6·103 + 2·102 + 9·101 + 3·100
Слайд 8История двоичной системы счисления
Двоичная система счисления была придумана математиками и
философами ещё до появления компьютеров (XVII — XIX вв.).
Пропагандистом
двоичной системы был знаменитый Г.В. Лейбниц. Он отмечал особую простоту алгоритмов арифметических действий в двоичной арифметике в сравнении с другими системами и придавал ей определенный философский смысл.В 1936 — 1938 годах американский инженер и математик Клод Шеннон нашёл замечательные применения двоичной системы при конструировании электронных схем.
Слайд 9Двоичная система счисления
Двоичная система счисления (бинарная
система счисления, binary) — позиционная
система счисления с основанием 2.Неудобством этой системы счисления является необходимость перевода исходных данных из десятичной системы в двоичную при вводе их в машину и обратного перевода из двоичной в десятичную при выводе результатов вычислений.
Главное достоинство двоичной системы — простота алгоритмов сложения, вычитания, умножения и деления.
Слайд 11Двоичное кодирование в компьютере
В конце ХХ века, века компьютеризации,
человечество пользуется двоичной системой
ежедневно, так как вся информация, обраба- тываемая современными ЭВМ, хранится в них в двоичном виде.В современные компьютеры мы можем вводить текстовую информацию, числовые значения, а также графическую и звуковую информацию. Количество информации, хранящейся в ЭВМ, измеряется ее «длиной» (или «объемом»), которая выражается в битах (от английского binary digit – двоичная цифра).
Слайд 13Заключение
Высшим достижением древней арифметики является открытие позиционного принципа представления чисел.
Нужно признать важность не только самой распространенной системы, которой мы
пользуемся ежедневно. Но и каждой по отдельности. Ведь в разных областях используются разные системы счисления, со своими особенностями и характерными свойствами. Слайд 15Перевод двоичного числа в десятичное
Для перевода двоичного числа в десятичное
необходимо его записать в виде многочлена, состоящего из произведений цифр
числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:Х10= Аn·2n-1 + Аn-1·2n-2 + Аn-2·2n-3 +…+А2·21 + А1·20
Перевод чисел
Слайд 16Перевод восьмеричного числа в десятичное
Для перевода восьмеричного числа в десятичное
необходимо его записать в виде многочлена, состоящего из произведений цифр
числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:Х10= Аn·8n-1 + Аn-1·8n-2 + Аn-2·8n-3 +…+А2·81 + А1·80
Перевод чисел
Слайд 17Перевод шестнадцатеричного числа в десятичное
Для перевода шестнадцатеричного числа в десятичное
необходимо его записать в виде многочлена, состоящего из произведений цифр
числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:Х10= Аn·16n-1 + Аn-1·16n-2 + Аn-2·16n-3 +…+А2·161 + А1·160
Перевод чисел
Слайд 18Перевод десятичного числа в двоичную систему
Для перевода десятичного числа в
двоичную систему его необходимо последовательно делить на 2 до тех
пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.Пример: Число 2210 перевести в двоичную систему счисления: 2210=101102
Перевод чисел
Слайд 19Перевод десятичного числа в восьмеричную систему
Для перевода десятичного числа в
восьмеричную систему его необходимо последовательно делить на 8 до тех
пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.Пример: Число 57110 перевести в восьмеричную систему счисления: 57110=10738
Перевод чисел
Слайд 20Перевод десятичного числа в шестнадцатеричную систему
Для перевода десятичного числа в
шестнадцатеричную систему его необходимо последовательно делить на 16 до тех
пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.Пример: Число 746710 перевести в шестнадцатеричную систему счисления: 746710=1D2B16
Перевод чисел
Слайд 21Перевод чисел из двоичной системы в восьмеричную
Чтобы перевести число из
двоичной системы в восьмеричную, его нужно разбить на триады (тройки
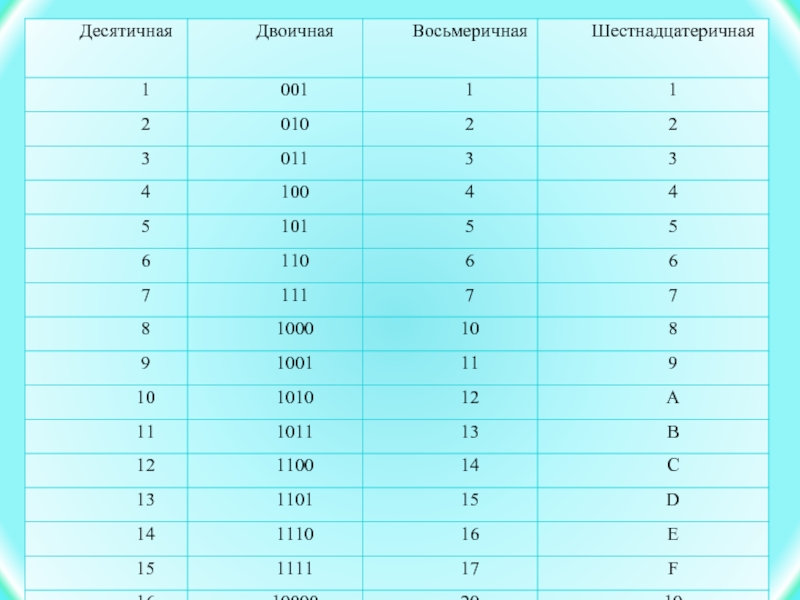
цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой. При переводе необходимо пользоваться двоично-восьмеричной таблицей:Пример: Число 10010112 перевести в восьмеричную систему счисления:
001 001 0112=1138
Перевод чисел
Слайд 22Перевод из двоичной системы в шестнадцатеричную
Чтобы перевести число из двоичной
системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр).
Двоично-шестнадцатеричная
таблица:Пример: Число 10111000112 перевести в шестнадцатеричную систему счисления:
0010 1110 00112=2E316
Перевод чисел
Слайд 23Перевод восьмеричного числа в двоичное
Для перевода восьмеричного числа в двоичное
необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
Пример: Число 5318
перевести в двоичную систему счисления:5318=101 011 0012
Перевод чисел
Слайд 24Перевод шестнадцатеричного числа в двоичное
Для перевода шестнадцатеричного числа в двоичное
необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
Пример: Число ЕЕ816
перевести в двоичную систему счисления:ЕЕ816=1110111010002
Перевод чисел
Слайд 25Перевод из восьмеричной системы счисления в шестнадцатеричную и обратно
При переходе
из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный
перевод чисел в двоичную систему.Пример 1: Число FEA16 перевести в восьмеричную систему счисления:
FEA16=1111111010102=111 111 101 0102=77528
Пример 2: Число 66358 перевести в шестнадцатеричную систему счисления:
66358=1101100111012=1101 1001 11012=D9D16
Перевод чисел
Слайд 26Единичная система
В древние времена, когда появилась потребность в записи чисел,
количество предметов, изображалось нанесением черточек или засечек на какой-либо твердой
поверхности.Археологами найдены такие «записи» при раскопках культурных слоев, относящихся к периоду палеолита (10–11 тысяч лет до н.э.).
В такой системе применялся только один вид знаков – палочка. Каждое число обозначалось с помощью строки, составленной из палочек, количество которых равнялось обозначаемому числу.
Древние системы счисления
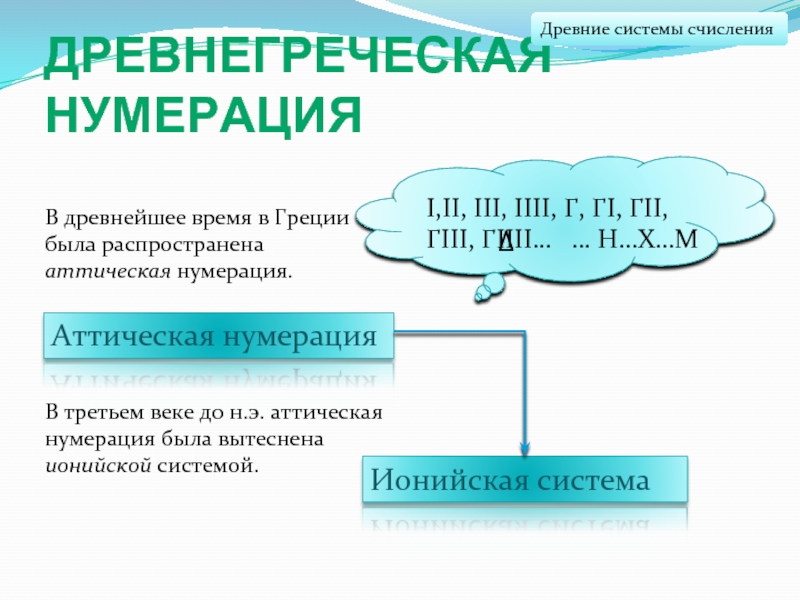
Слайд 27Древнегреческая нумерация
Аттическая нумерация
Ионийская система
В третьем веке до н.э. аттическая нумерация
была вытеснена
ионийской системой.
В древнейшее время в Греции была распространена
аттическая нумерация.Древние системы счисления
Слайд 28Славянская нумерация
В России славянская нумерация сохранилась до конца XVII века.
Южные и восточные славянские народы для записи чисел пользовались алфавитной
нумерацией. Славянская нумерация сохранялась только в богослужебных книгах. Над буквой, обозначавшей цифру, ставился специальный значок: («титло»). Для обозначения тысяч перед числом (слева внизу) ставился особый знак .Z
Древние системы счисления
Слайд 29Римская нумерация
Древние римляне пользовались нумерацией, которая сохраняется до настоящего времени
под именем «римской нумерации». Мы пользуемся ей для обозначения веков,
юбилейных дат, наименования съездов и конференций, для нумерации глав книги или строф стихотворения.Запись цифр в римской нумерации:
Древние системы счисления