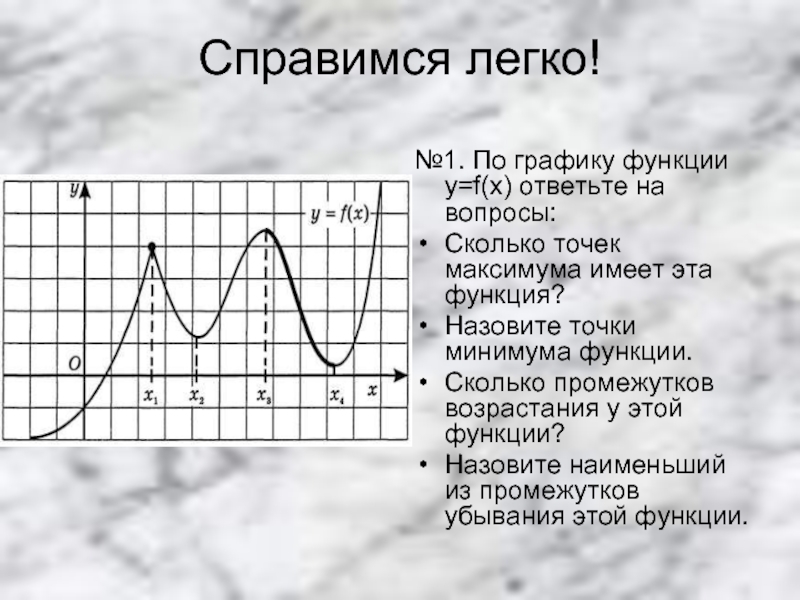
максимума имеет эта функция?
Назовите точки минимума функции.
Сколько промежутков возрастания у
этой функции?Назовите наименьший из промежутков убывания этой функции.









![Применение производной для исследования функции №1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён №1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её производной. Укажите количество](/img/thumbs/a2fea71c92172823391f31bd9a325c23-800x.jpg)