Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Степенные функции
Содержание
- 1. Степенные функции
- 2. Эпиграфом нашего урока являются слова А. Эйнштейна:
- 3. План: 1.Введение (определение) 1.1 Область определения 1.2
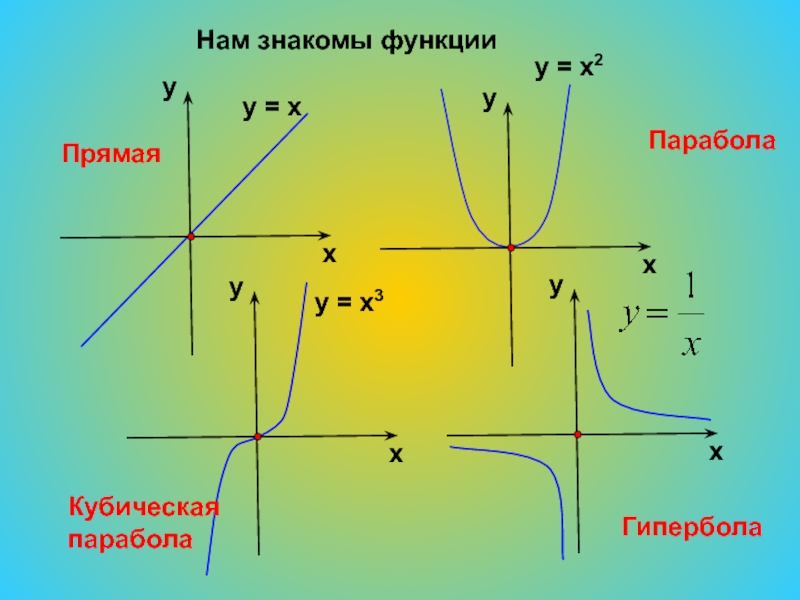
- 4. Нам знакомы функцииПрямаяПараболаКубическая параболаГипербола
- 5. Степенными функциями называются функции вида у = хr, где r – заданное рациональное числоВведение
- 6. 1.1. Область определения Если показатель степени —
- 7. 1.2. Рациональный показатель степениГрафики степенной функции при
- 8. 1.3. Свойства Функция непрерывна и неограниченно
- 9. Слайд 9
- 10. Если а=0, то степень х0 определена для
- 11. Если а=1, то получим функцию у = х, её графиком является прямая.
- 12. yx -1 0 1 2у
- 13. Показатель r = 2n – чётное натуральное
- 14. yx -1 0 1 2у
- 15. Показатель r = 2n-1 – нечётное
- 16. yx -1 0 1 2у
- 17. Показатель r = – (2n-1), где n
- 18. yx -1 0 1 2у
- 19. Показатель r = – 2n, где n
- 20. yx -1 0 1 2у
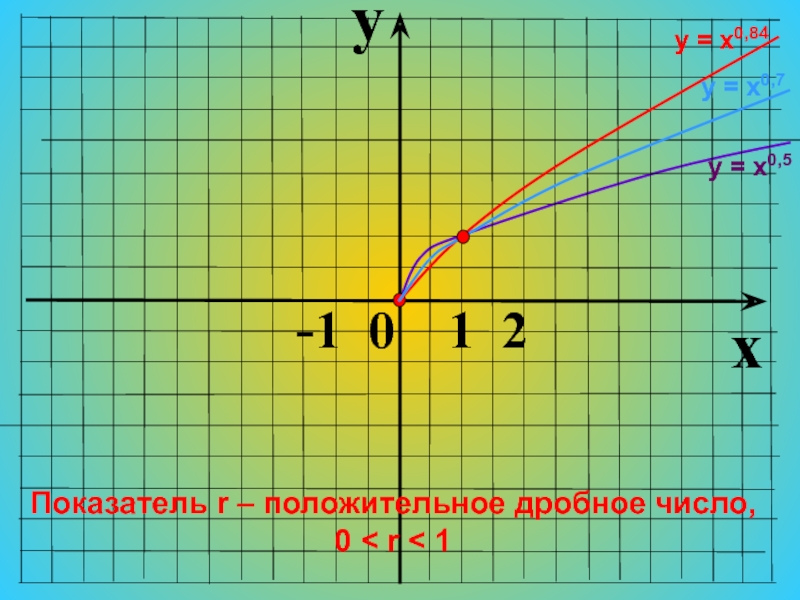
- 21. 0Показатель r – положительное дробное число, 0
- 22. yx -1 0 1 2Показатель
- 23. yx -1 0 1 2Показатель
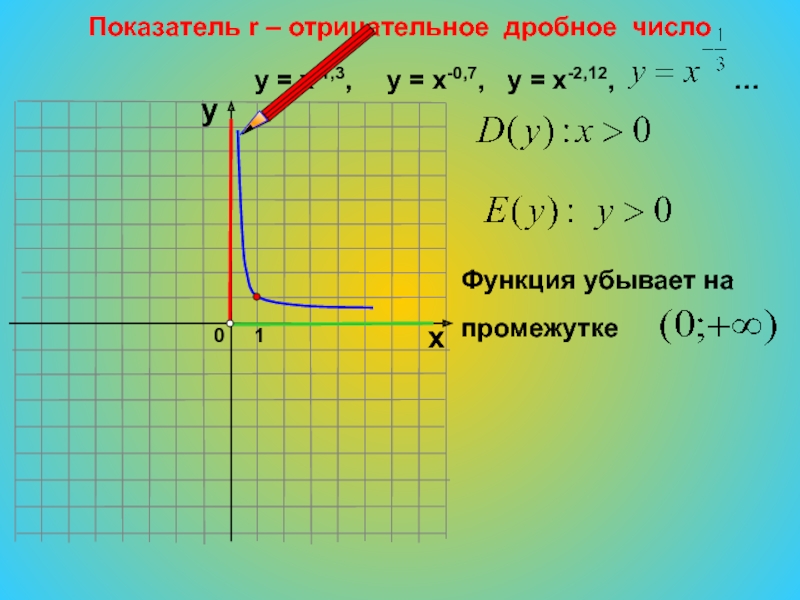
- 24. 0Показатель r – отрицательное дробное число1хуу =
- 25. Примеры решения степенных функцийФункцияГрафик функции- кубическая парабола.1)
- 26. Число a- отвечает за перемещение вдоль оси
- 27. График функции- гипербола.1) Д(y)=R, кроме х=02)
- 28. Число а- отвечает за перемещение вдоль оси
- 29. Функция 1) Д(y)=
- 30. Сегодня на урокемы расширили знания о степенных функциях, их свойствах и графиках
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3План:
1.Введение (определение)
1.1 Область определения
1.2 Рациональный показатель степени
1.3 Свойства
2 Комплексная функция
Литература
Примечания
Слайд 5Степенными функциями называются функции вида у = хr, где r
– заданное рациональное число
Введение
Слайд 61.1. Область определения
Если показатель степени — целое число, то можно
рассматривать степенную функцию на всей числовой прямой (кроме, возможно, нуля).
В общем случае степенная функция определена при x > 0. Если a > 0, то функция определена также и при x = 0, иначе нуль является её особой точкой.Слайд 71.2. Рациональный показатель степени
Графики степенной функции при натуральном показателе n
называются параболами порядка n. При a = 1 получается функция
y = kx, называемая прямой пропорциональной зависимостью.Графики функций вида y = x − n, где n — натуральное число, называются гиперболами порядка n. При a = − 1 получается функция , называемая обратной пропорциональной зависимостью.
Если , то функция есть арифметический корень степени n.
Пример: из третьего закона Кеплера вытекает, что период T обращения планеты вокруг Солнца связан с большой полуосью A её орбиты соотношением: T = kA3 / 2 (полукубическая парабола).
Гиперболы порядка n:
n = − 1
n = − 2
n = − 3
Параболы порядка n:
n = 0
n = 1
n = 2
n = 3
n = 4
Гиперболы порядка n:
n = − 1
n = − 2
n = − 3
Слайд 8
1.3. Свойства
Функция непрерывна и неограниченно дифференцируема всюду, где она определена.
В
интервале
, функция монотонно возрастает при a > 0 и монотонно убывает при a < 0. Значения функции в этом интервале положительны.Производная функции:
Слайд 9 Алгоритм решения Рассмотрим степенные функции с натуральным показателем а, принадлежащим ко
множеству всех натуральных чисел. Если а≠0, то в степень а
можно возвести любое действительное число. Поэтому областью определения функции у =xа является множество всех действительных чисел. С некоторыми такими степенными функциями с натуральным показателем мы уже знакомы.
Слайд 10Если а=0, то степень х0 определена для любого числа х≠0.
При этом х0=1 функция у=х0 определена на множестве Х=(-∞; 0)
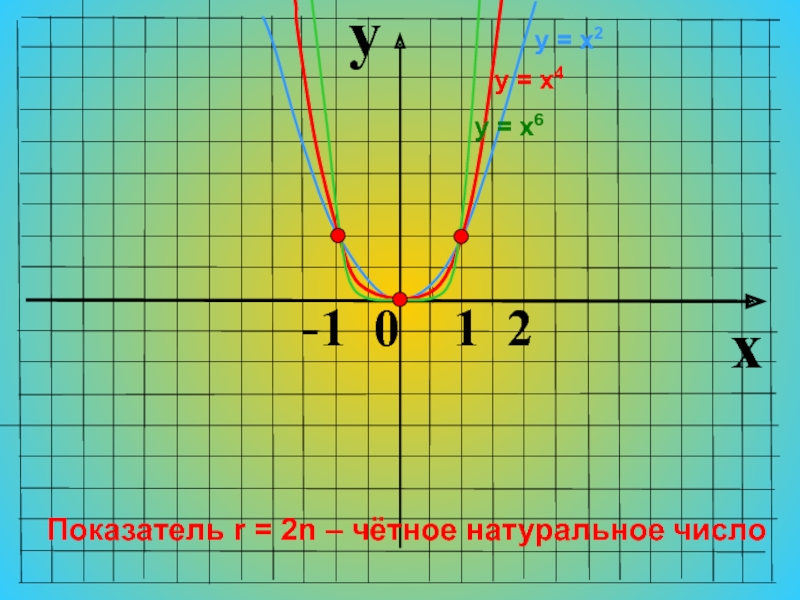
и (0;∞) и её графиком является параллельная оси Ох прямая у=1 с одной «выколотой» точкой (0;1). Слайд 13Показатель r = 2n – чётное натуральное число
0
х
у
у = х2,
у = х4 , у =
х6, у = х8, …у = х2n
Функция у=х2n чётная,
т.к. (–х)2n = х2n
График чётной функции
симметричен относительно
оси Оу.
Слайд 15Показатель r = 2n-1 – нечётное натуральное число
х
у
у =
х3, у = х5, у =
х7, у = х9, …у = х2n-1
Функция у=х2n-1 нечётная,
т.к. (–х)2n-1 = – х2n-1
0
График нечётной функции симметричен относительно начала координат – точки О.
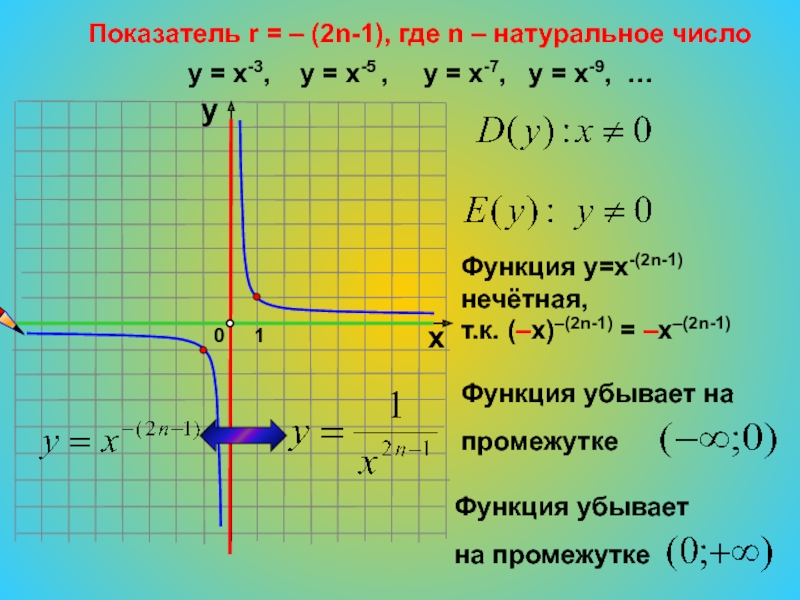
Слайд 17Показатель r = – (2n-1), где n – натуральное число
1
0
х
у
у
= х-3, у = х-5 ,
у = х-7, у = х-9, …Функция у=х-(2n-1) нечётная,
т.к. (–х)–(2n-1) = –х–(2n-1)
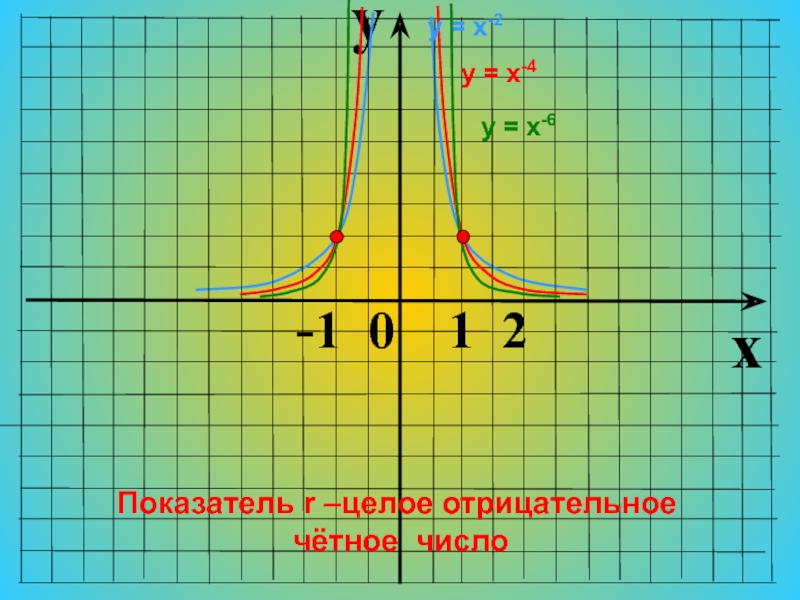
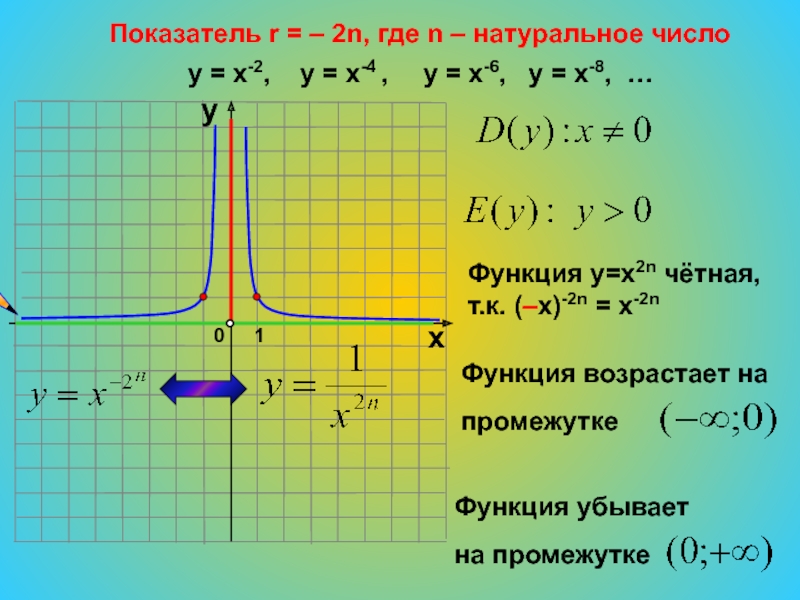
Слайд 19Показатель r = – 2n, где n – натуральное число
1
0
х
у
у
= х-2, у = х-4 ,
у = х-6, у = х-8, …Функция у=х2n чётная,
т.к. (–х)-2n = х-2n
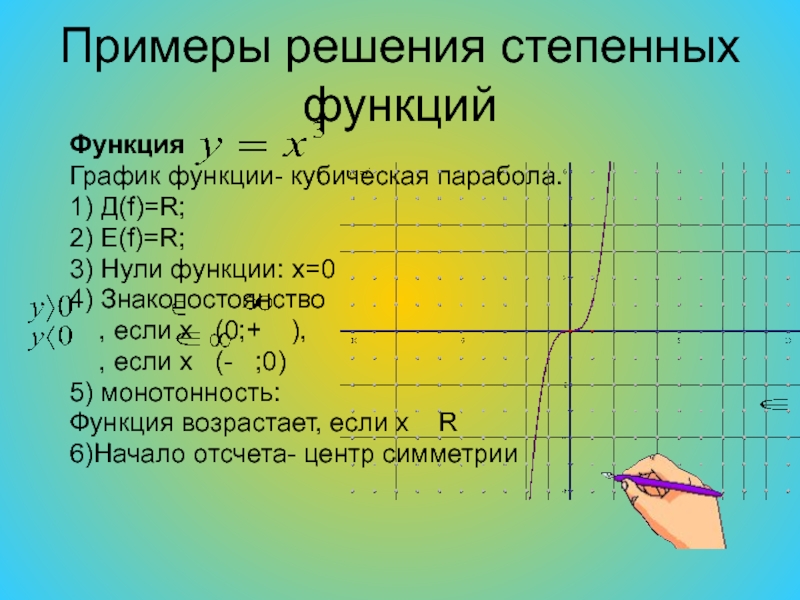
Слайд 25Примеры решения степенных функций
Функция
График функции- кубическая парабола.
1) Д(f)=R;
2) E(f)=R;
3) Нули
функции: x=0
4) Знакопостоянство
, если x (0;+
),, если x (- ;0)
5) монотонность:
Функция возрастает, если x R
6)Начало отсчета- центр симметрии
Слайд 26
Число a- отвечает за перемещение вдоль оси ОХ;
если а 0,
то влево на а единиц от 0;
если а 0,
то
вправо на а единиц от 0.Число b-отвечает за перемещение вдоль оси OY;
если b 0,
то вверх на b единиц от 0 ;
если b 0,
то вниз на b единиц от 0.
Слайд 27
График функции- гипербола.
1) Д(y)=R, кроме х=0
2) E(y)=R, кроме
y=0
3) Нули функции: нет
4) Знакопостоянство:
, если
,, если
5) монотонность:
Функция убывает на всей области определения
6)Начало отсчета- центр симметрии.
Слайд 28
Число а- отвечает за перемещение вдоль оси OX;
если
,
то влево на a единиц от 0;
если
,то вправо на а единиц от 0.
Число b- отвечает за перемещение вдоль оси OY;
если ,
то вверх на b единиц от 0;
если ,
то вниз на b единиц от 0.
Слайд 29Функция
1) Д(y)=
2)E(y)=
3) Нули функции x=0
4)
Знакопостоянство: , если
5) монотонность:
Функция возрастает,
если