TheSlide.ru

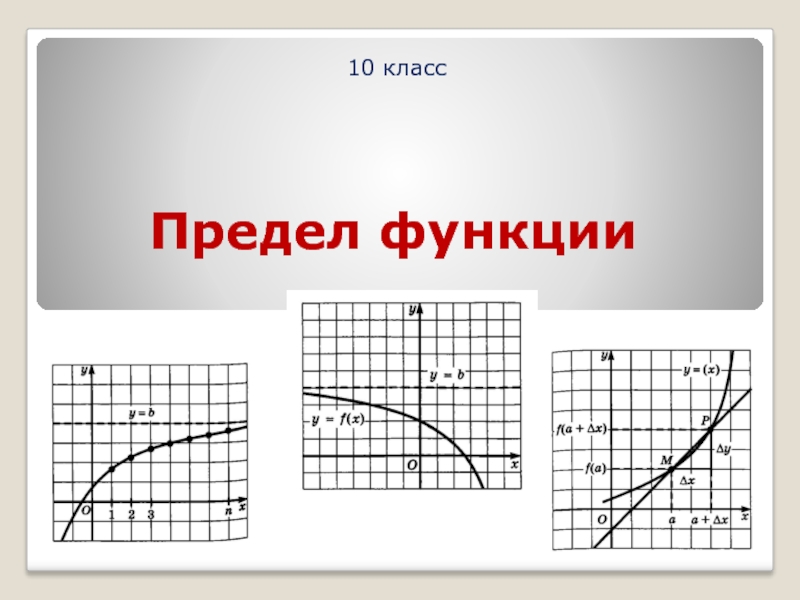
Способы задания функций

Содержание

1. Способы задания функций
2. Способы: Путем параллельного переноса вдоль оси
3. 1)Параллельный перенос на вектор с координатами (0;
4. yх0Y=sinХ+2Y=sinХ2Пример А
5. хy0-5Y=Х2 Y=Х2 - 5 Пример В
6. Растяжение вдоль оси ОY с коэффициентом K,
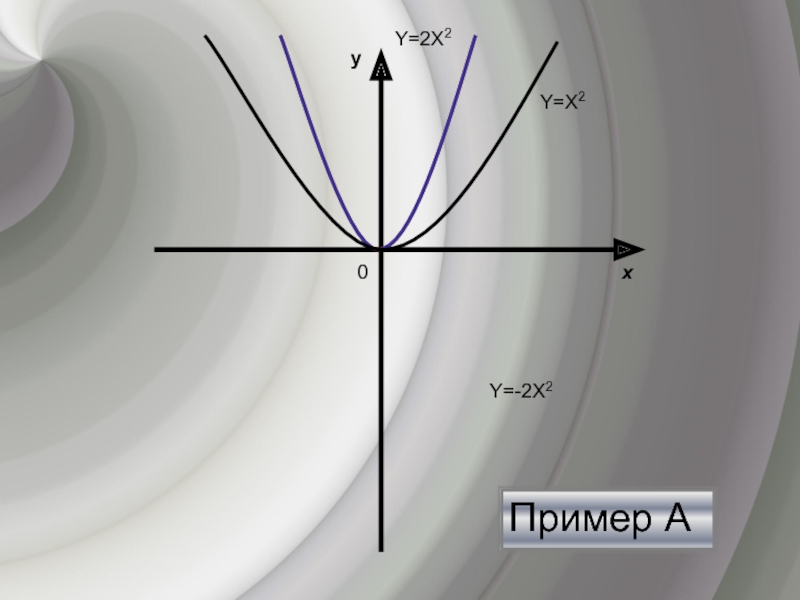
7. Пример Ахy0Y=Х2 Y=-2Х2 Y=2Х2
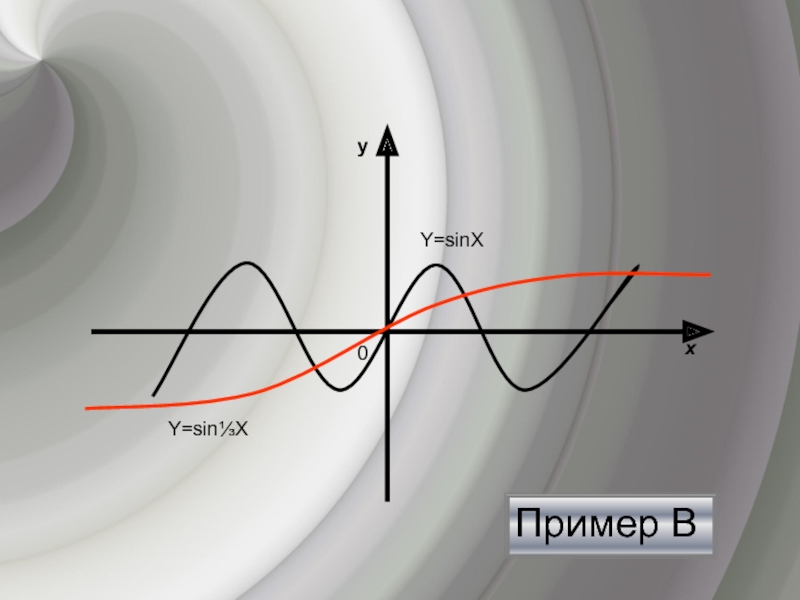
8. Пример ВПример Вyх0Y= ⅓sinХY=sinХ
9. Параллельный перенос вдоль оси абсцисс на вектор
10. Пример Ахy0Y=√Х Y= √Х-1 Y= √Х+1 -11
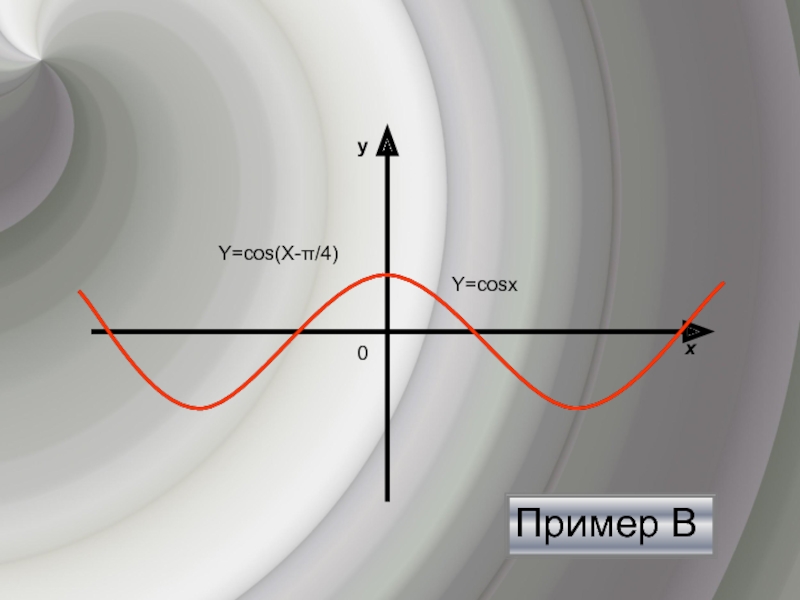
11. Пример Вyх0Y=cosхY=cos(Х-π/4)
12. Растяжение вдоль оси х с коэффициентом K
13. Пример Аyх0Y=cosХY=cos2Х
14. Пример Вyх0Y=sinХY=sin⅓Х
15. Успехов в учебе!
16. Скачать презентанцию

Способы: Путем параллельного переноса вдоль оси ординатПутем растяжения вдоль ОYПараллельным переносом вдоль оси абсцисс Путем растяжения вдоль оси Х с коэффициентом K

Главная
Алгебра
Способы задания функций

Слайды и текст этой презентации

Слайд 1«Способы задания функций»

«Способы задания функций»

Слайд 2 Способы:
Путем параллельного переноса вдоль оси ординат
Путем растяжения вдоль

ОY
Параллельным переносом вдоль оси абсцисс
Путем растяжения вдоль оси Х

с коэффициентом K

Способы: Путем параллельного переноса вдоль оси ординатПутем растяжения вдоль ОYПараллельным переносом вдоль оси абсцисс Путем растяжения

Слайд 31)
Параллельный перенос на вектор с координатами (0; b) вдоль оси

ординат который будет задаваться формулой (х;f (х)) → (х;f (х)+b)

Для построения графика (х;f (х)+b), где b – постоянное число, надо перенести график f на вектор (0; b) вдоль оси ординат

1)Параллельный перенос на вектор с координатами (0; b) вдоль оси ординат который будет задаваться формулой (х;f (х))

Слайд 4y
х
0
Y=sinХ+2
Y=sinХ
2
Пример А

yх0Y=sinХ+2Y=sinХ2Пример А

Слайд 5х
y
0
-5

Y=Х2
Y=Х2 - 5
Пример В

хy0-5Y=Х2 Y=Х2 - 5 Пример В

Слайд 6Растяжение вдоль оси ОY с коэффициентом K, который задается формулами

Х`=Х; Y`=KY
( х;f (х)) → ( х;f к(х) )

Для построения y= кf(х) надо растянуть график функции y= f(х) в к раз вдоль оси ординат

2)

Растяжение вдоль оси ОY с коэффициентом K, который задается формулами Х`=Х; Y`=KY ( х;f (х)) → (

Слайд 7Пример А
х
y
0

Y=Х2
Y=-2Х2

Y=2Х2

Пример Ахy0Y=Х2 Y=-2Х2 Y=2Х2

Слайд 8Пример В

Пример В
y
х
0
Y= ⅓sinХ
Y=sinХ

Пример ВПример Вyх0Y= ⅓sinХY=sinХ

Слайд 9Параллельный перенос вдоль оси абсцисс на вектор с координатами (a;0)

с формулами Х`=Х; Y`=KY
(х+a;f (х)) → (х;f (х)+a)
График

y=f (х)-a получается путем переноса вдоль оси абсцисс на вектор (a;0), если a>0, то вектор направлен в противоположную сторону, a<0- отрицательную

3)

Параллельный перенос вдоль оси абсцисс на вектор с координатами (a;0) с формулами Х`=Х; Y`=KY (х+a;f (х)) →

Слайд 10Пример А
х
y
0

Y=√Х
Y= √Х-1
Y= √Х+1

-1
1

Пример Ахy0Y=√Х Y= √Х-1 Y= √Х+1 -11

Слайд 11Пример В
y
х
0
Y=cosх
Y=cos(Х-π/4)

Пример Вyх0Y=cosхY=cos(Х-π/4)

Слайд 12Растяжение вдоль оси х с коэффициентом K задается формулами
Х`=KХ; Y`=Y
(х;f

(х)) → (х;f (х)/k)
Для построения y= f(х)/k) надо подвергнуть график

растяжению с коэффициентом k вдоль оси абсцисс

4)

Растяжение вдоль оси х с коэффициентом K задается формуламиХ`=KХ; Y`=Y(х;f (х)) → (х;f (х)/k)Для построения y= f(х)/k)

Слайд 13Пример А
y
х
0
Y=cosХ
Y=cos2Х

Пример Аyх0Y=cosХY=cos2Х

Слайд 14Пример В
y
х
0
Y=sinХ
Y=sin⅓Х

Пример Вyх0Y=sinХY=sin⅓Х

Слайд 15Успехов в учебе!

Успехов в учебе!

Скачать презентацию

Теги

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей