b], причём b – a > ε
Будем считать, что функция:
1)Непрерывна
и монотонна на отрезке [a, b]2)f (a) x f (b) < 0
Итак разделим отрезок [a, b] пополам, середина отрезка c = (a + b) / 2
Отрезок [a, b] разделен на два отрезка [a, c] и [c, b], длина каждого = (b – a) / 2


![Численные методы решения уравнений Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], Пусть корень ξ уравнения f (x) отделён на отрезке [a, b], причём b – a > εБудем](/img/thumbs/52d2c3e8a2e8625f24b562f5e7e1b505-800x.jpg)
![Численные методы решения уравнений xyabcC = (a + b) / 2a1b1c1a2b2c2b-a>ε[a; c] и [c; b], xyabcC = (a + b) / 2a1b1c1a2b2c2b-a>ε[a; c] и [c; b], длина отрезков (b - a) /](/img/thumbs/001219d93734a274ed21519c1b75ff6a-800x.jpg)


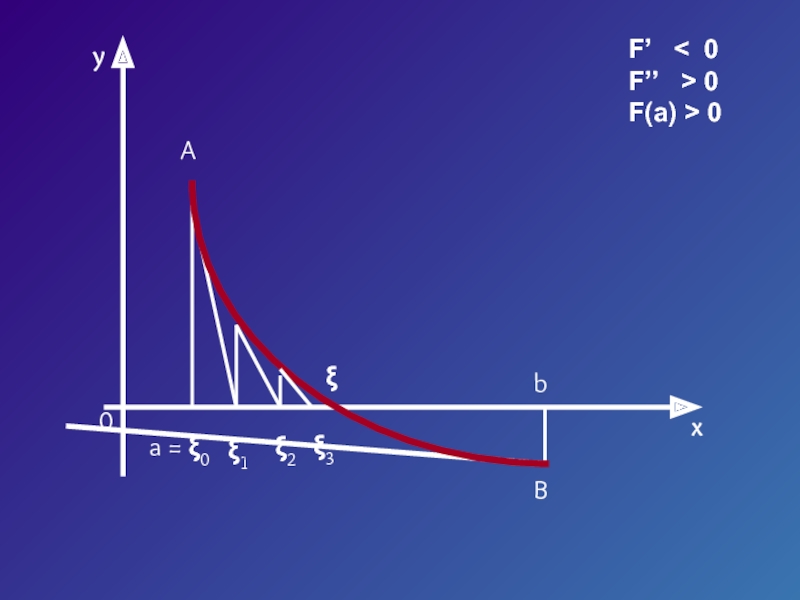
![Численные методы решения уравнений Пусть корень уравнения F (x) = 0 отделен на отрезке [a, Пусть корень уравнения F (x) = 0 отделен на отрезке [a, b].Будем считать:F (x) непрерывна на отрезке](/img/thumbs/6c96400d17b44750c264b2baa8b567f7-800x.jpg)
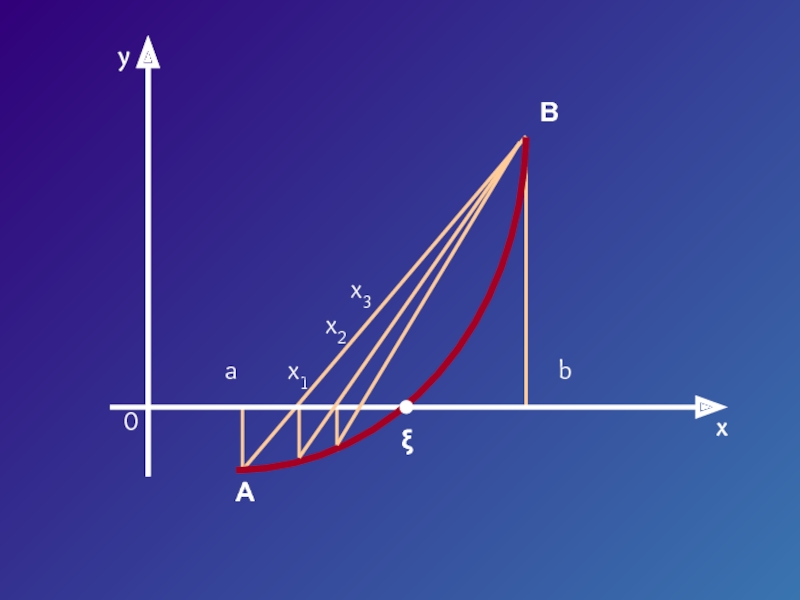


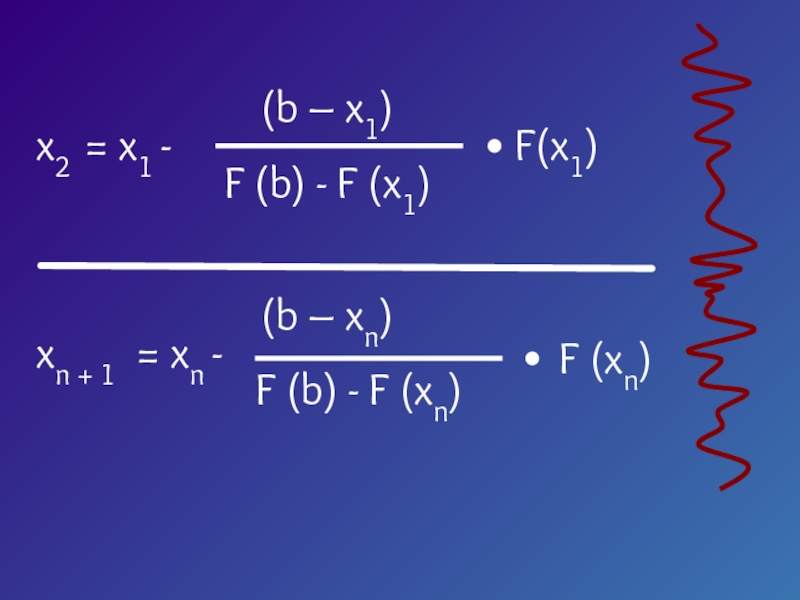
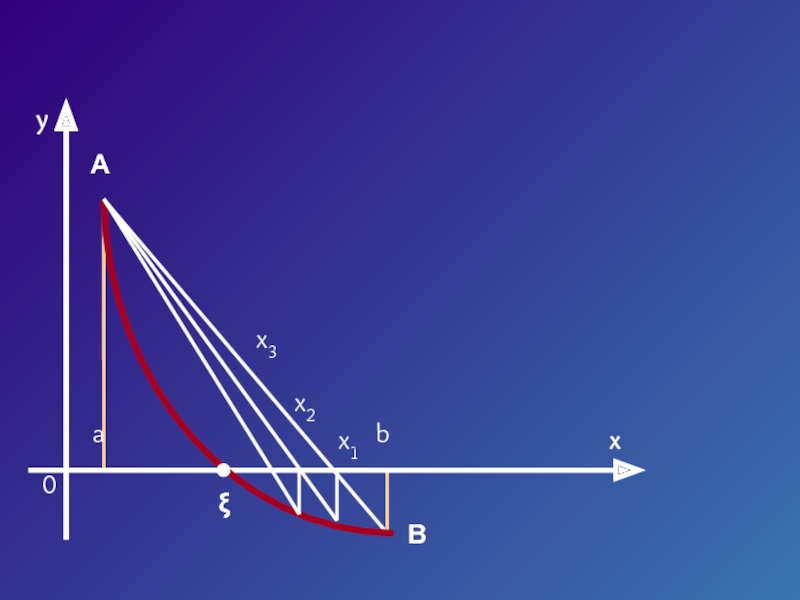
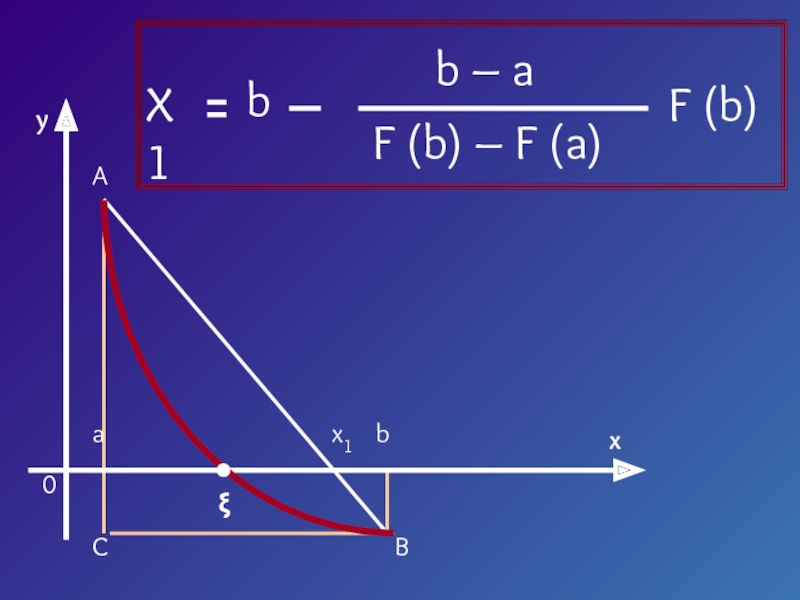

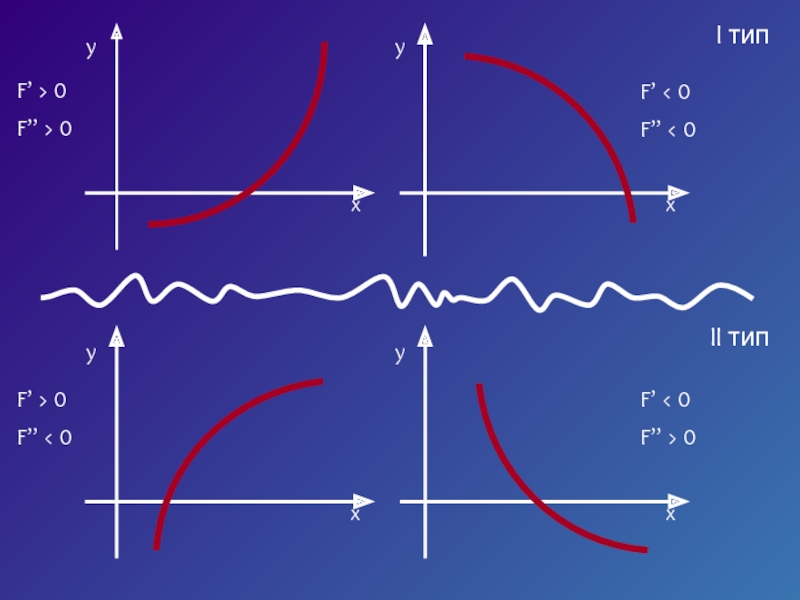
![Численные методы решения уравнений Пусть корень ξ уравнения F (x) = 0 отделен на отрезке Пусть корень ξ уравнения F (x) = 0 отделен на отрезке [a, b].Будем считать:F (x) непрерывна на](/img/thumbs/c8914911c81cc423abfd5bdd6be252f7-800x.jpg)