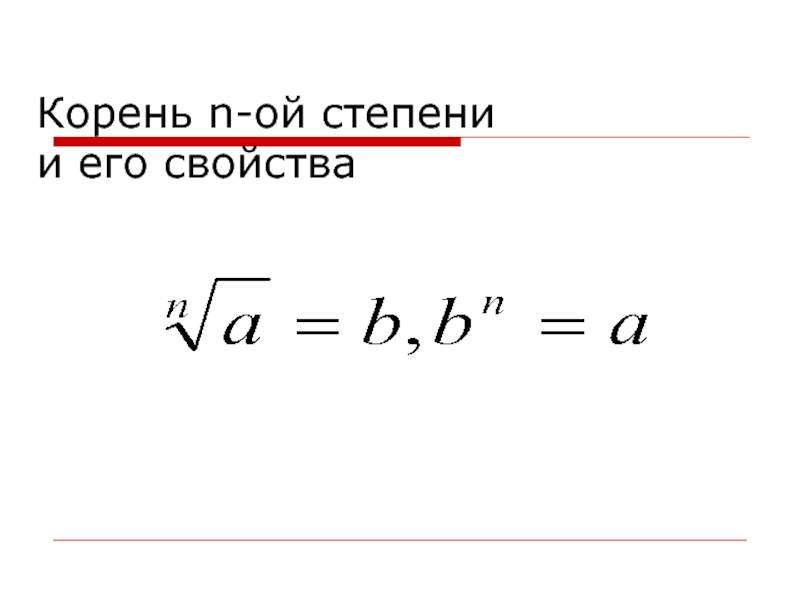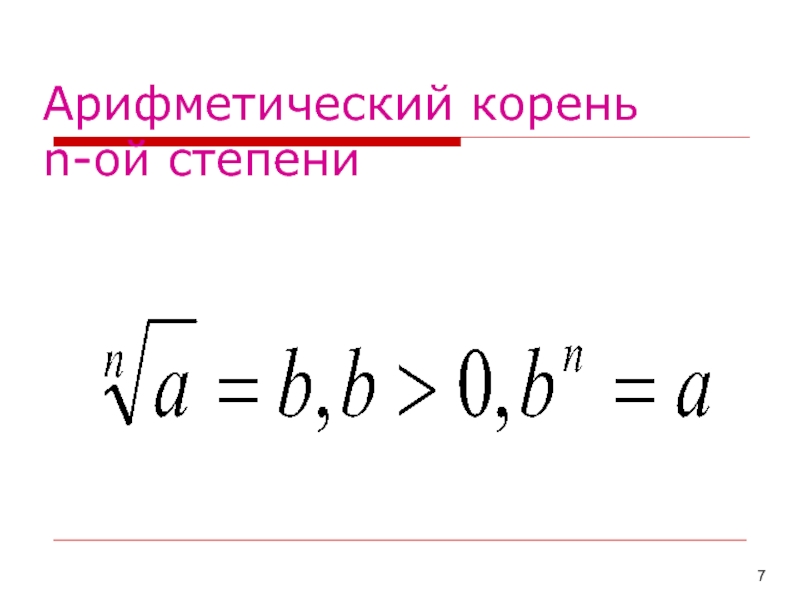Корень n-й степени и его свойства

Содержание

1. Корень n-й степени и его свойства
2. Задание №1Используя график, ответить на вопросы:1. Сколько корней имеет уравнение х5=7?2. Чему равны эти корни?
3. Задание №2Используя график, ответить на вопросы:График четной
4. Задание №3При каком значении параметра «а» уравнение
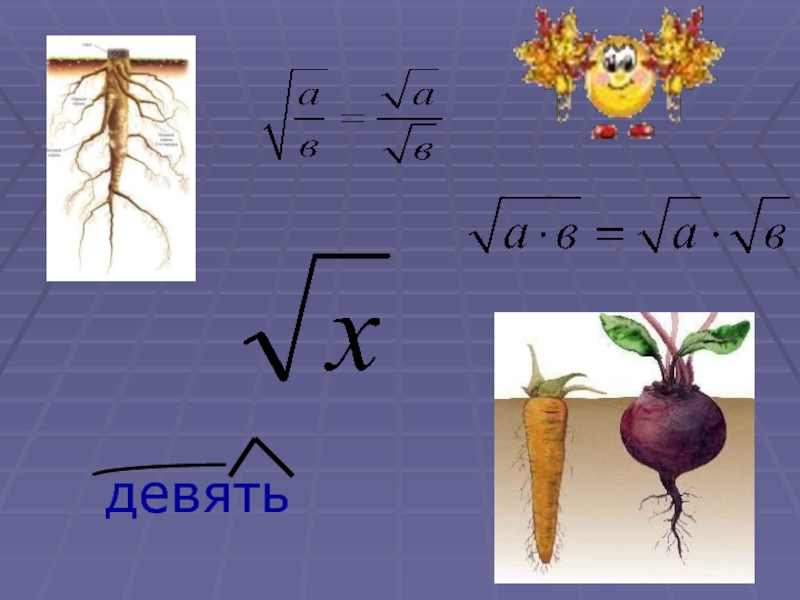
5. Напомним основные свойства арифметических корней (иногда их
6. Корень n-ой степени и его свойства
7. Арифметический корень n-ой степени
8. Свойства корней
9. Покажем на примерах, как используются свойства корней и рациональных степеней в вычислениях.Пример 1. Вычислить
10. По свойству №5:.Подставим результаты вычислений из
11. Решить уравнение
12. Ход решения уравненияЗамена:
13. Обобщение материала 1. С каким математическим понятием
14. Пауза!!! (Упражнения для глаз)
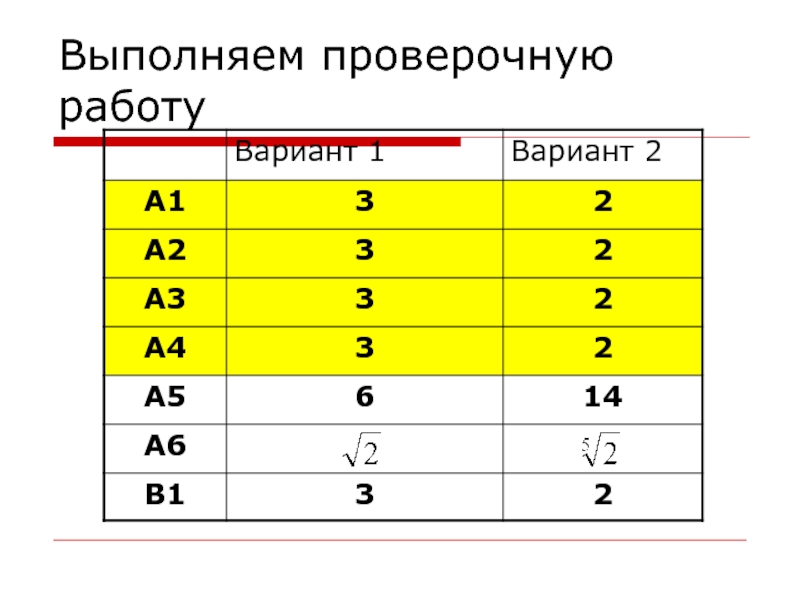
15. Выполняем проверочную работу
16. Домашнее заданиеЕсли справились полностью Изучить
17. Самостоятельная работаОценка «3»I вариант1. Найти значение числового
18. Самостоятельная работаI вариант1.а) 11б) 152.
19. Самостоятельная работаОценка «3»1. Найти значение числового выражения:а)
20. Самостоятельная работа1.а) 13 б) 62.
21. Самостоятельная работаОценка «4»1. Решить уравнениеа)б) 2. Упростить выражение Оценка «5»Избавиться от иррациональности в знаменателеа)б)
22. Самостоятельная работаОтветыОценка «4»1.а) б) 2. 0Оценка
23. Всем большое спасибо за урок
24. Скачать презентанцию

Задание №1Используя график, ответить на вопросы:1. Сколько корней имеет уравнение х5=7?2. Чему равны эти корни?

Главная
Алгебра
Корень n-й степени и его свойства

Слайды и текст этой презентации

Слайд 1Корень n-й степени и его свойства
Цель урока:

Ввести понятие корня

n-ой степени;
рассмотреть примеры вычисления корней n-ой степени;
познакомиться с

решением уравнений вида хn = a

Корень n-й степени и его свойстваЦель урока: Ввести понятие корня n-ой степени; рассмотреть примеры вычисления корней

Слайд 2Задание №1
Используя график, ответить на вопросы:

1. Сколько корней имеет

уравнение х5=7?

2. Чему равны эти корни?

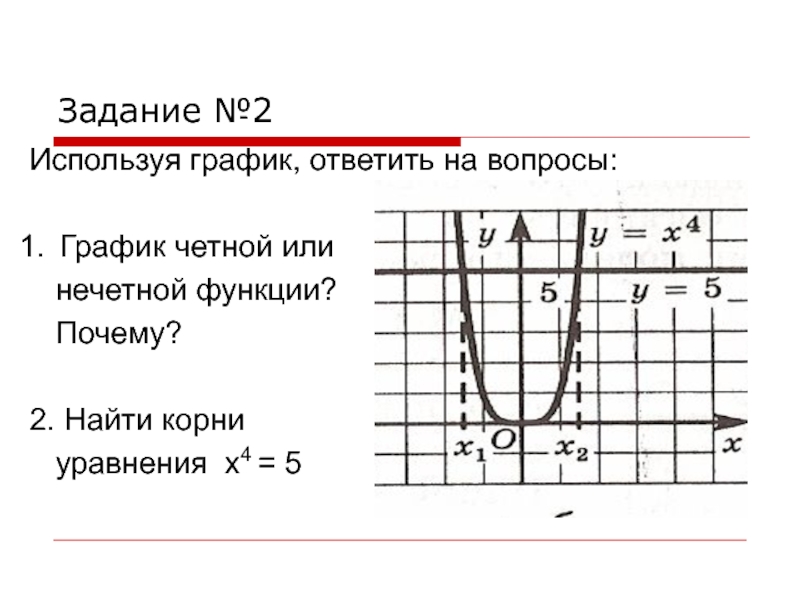
Слайд 3Задание №2
Используя график, ответить на вопросы:

График четной или

нечетной функции?
Почему?

2. Найти корни
уравнения х4

= 5

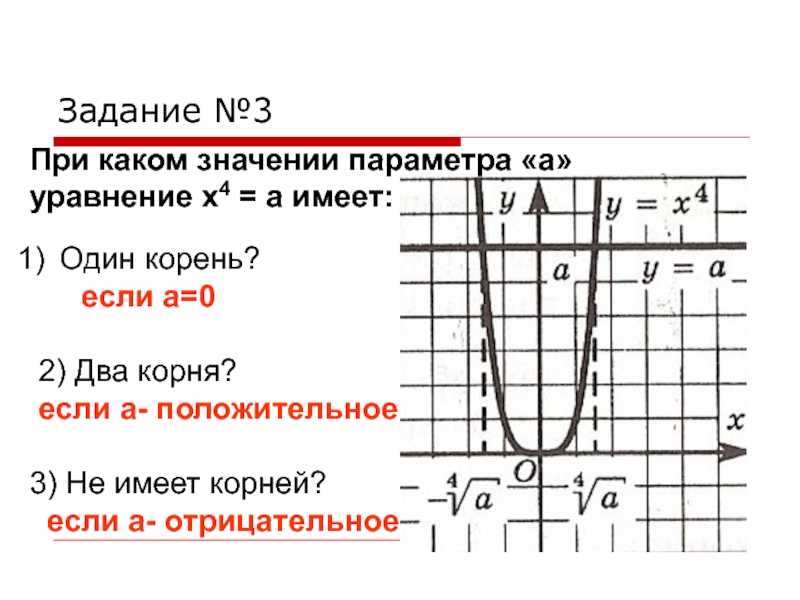
Задание №2Используя график, ответить на вопросы:График четной или нечетной функции? Почему?2. Найти корни уравнения

Слайд 4Задание №3
При каком значении параметра «а»
уравнение х4 = а

имеет:

Один корень?
если а=0

2) Два корня?
если

а- положительное

3) Не имеет корней?
если а- отрицательное

Задание №3При каком значении параметра «а» уравнение х4 = а имеет:Один корень? если а=0 2)

Слайд 5
Напомним основные свойства арифметических корней (иногда их называют свойствами корней

n-ой степени). Все они верны и для квадратных корней, так

как :
для .
Это важнейшее свойство, которое позволяет переходить от корней к рациональным степеням. После такого перехода можно пользоваться всеми свойствами степеней.

Напомним основные свойства арифметических корней (иногда их называют свойствами корней n-ой степени). Все они верны и для

Слайд 6Корень n-ой степени и его свойства

Слайд 7Арифметический корень n-ой степени

Слайд 8Свойства корней

Слайд 9Покажем на примерах, как используются свойства корней и рациональных степеней

в вычислениях.
Пример 1. Вычислить

Слайд 10
По свойству №5:
.
Подставим результаты вычислений из 1) и 2)

в выражение

Здесь мы использовали свойства №2 и №8 арифметических корней.

Ответ: 2.

Решение. 1) Упростим сначала первую часть выражения.
Используя свойство №3, получим
.
Теперь применим свойства №6 и №5:
.

Применим теперь свойство №1:
В итоге мы получили:

По свойству №5:
.
Подставим результаты вычислений из 1) и 2) в выражение

Здесь мы использовали свойства №2 и №8 арифметических корней.

Ответ: 2.

Слайд 11Решить уравнение

Слайд 12Ход решения уравнения
Замена: а;

0,5а +

13 + 0,2а = 2а;
- 1,3а = - 13;
а =

10;
Обратная замена: 10;
5х = 1000;
х = 200.
Ответ: 200.

Ход решения уравненияЗамена: а;0,5а + 13 + 0,2а = 2а;- 1,3а =

Слайд 13Обобщение материала
1. С каким математическим понятием мы работали сегодня

корень n–ой степени
2. Что мы применяли для вычислений корня n–ой степени
свойства корня n–ой степени
3. Сколько корней имеет уравнение хn = а, если n – нечетное число (например: х7 = 5)
один корень
4. Сколько корней имеет уравнение хn= а, если n –четное число (например: х12=а)
зависит от а:
если а – отрицательное, то нет корней;
если а = 0, то один корень;
если а – положительное, то два корня.

Слайд 14Пауза!!! (Упражнения для глаз)

Слайд 15Выполняем проверочную работу

Слайд 16Домашнее задание
Если справились полностью
Изучить пункт 33,

Разобрать примеры №1 и №3 из учебника,

Выполнить №417(а,б), № 419 (а,б).

Если допущены ошибки в дополнительной части работы №394, 410 (а)

Если допущены ошибки в обязательной части работы №391-393(а,б)